Professeurs tournesols

"La question, à présent, c'est "Mais pourquoi ?". Et la réponse que je donne pour l'instant, c'est "Je sais pas, laissez-moi faire des recherches, vous saurez tout dans une prochaine note !"." [El Jj, 25/11/06]

Voici enfin venu le temps, non pas des rires et des champs, mais d'apprendre la vérité : pourquoi trouve t'on donc la suite de Fibonacci dans tous nos végétaux familiers (exepté le radis et certains autres fruits et légumes pas très rigolos).

(À noter après relecture survolage que cette note est bien longue pour en arriver là où il fallait arriver...)

Allez, rentrons directement dans le sujet, et interressons nous à la manière dont les fleurs poussent. Enfin, surtout au niveau des graines qui nous intéressent. Bref, la fleur pousse, et donc, de nouvelles graines apparaissent, et pour être un peu plus précis dans les termes, elles apparaissent au milieu de la fleur, autour du petit disque central répondant au nom de "apex". La fleur grandissant, de nouvelles graines apparaissent autour de l'apex, poussant les autres vers l'extérieur, faisant naître une radieuse fleur.
Petit détail important : les nouvelles graines apparaissent en formant par rapport à la graine qui l'a précédé un angle de environ 222,4922°. Pourquoi cet angle ? Chaque chose en son temps, vous le saurez (ou pas) en bas de cette note.

Pour l'instant, nous savons à peu près ça sur la pousse des graines des fleurs. Le schéma est suffisemment clair pour que je n'ai pas besoin de le commenter (et sur le coup, ça m'arrange).

Revenons en à notre angle, 222,4922°, aussi appelé angle d'or (, soit 360×1/). Imaginons maintenant un autre monde, où cet angle était un nombre rationnel, c'est à dire, un nombre de la forme p/q×360° (avec p et q entiers). Par exemple, un angle de 5/7×360°, soit un angle faisant les 5/7 d'un cercle. Après la pousse, les graines seraient disposées comme ça :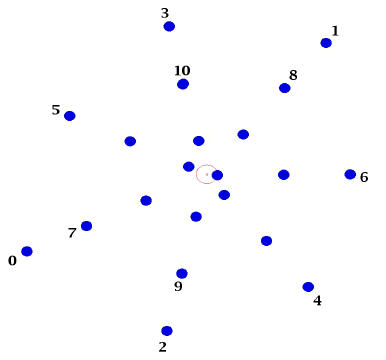

On le remarque tout de suite : les graines sont alignées. Forcément, avec un angle de 4/7×360°, au bout de 7 tours, on obtient un angle de 4×360° : on est revenu dans la direction originale. Avec un angle de p/q×360°, on arrivera toujours au bout de q tours au point de départ, ce qui perd un peu en jolieté (j'invente les mots dont j'ai besoin).
Avec un nombre irrationnel (qui ne puisse pas s'écrire sous la forme p/q), les choses sont bien différentes, puisque les graines ne se retrouveront jamais alignées. Prenons par exemple ×360°. Cela donne quelque chose comme ça :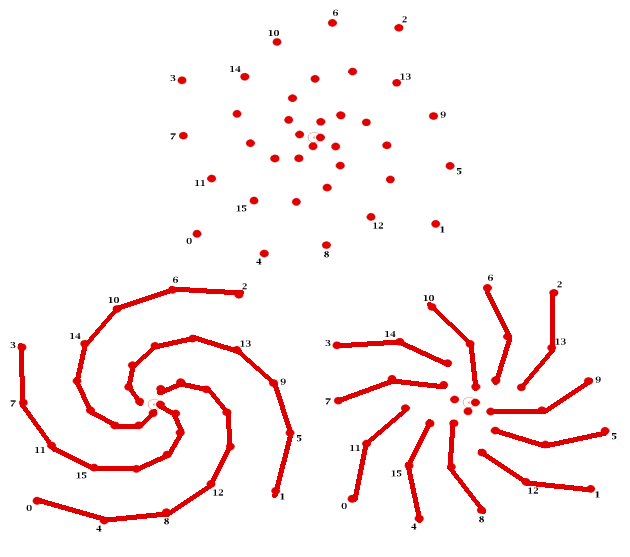

Et voilà c'est y pas qui apparait donc ! Des parastiches spirales ! 4 dans un sens et 11 dans l'autres (moins visibles, certes). Tout ceci est très joli, mais quid des suites de Fibonacci ? Venons-on donc à un angle de 360*1/. Cela va donc donner ceci :

En vert, on a bien 13 parastiches (ex : 0 - 13 - 26 - 39), et en rouge, on en a 21 (ex : 0 - 21 -42).

Pour compter le nombre de paratiches avec un angle irrationnel, il suffit juste de regarder le numéro des points les plus proches de 0. Dans l'exemple avec l'angle d'or, on a bien le point 13 et le point 21. Dans l'exemple de ×360°, on a les points 11 et 4 les plus proches du point 0. Cette règle est générale à tous les exemples d'angles irrationnels . Pourquoi ? Dans l'exemple de l'angle d'or, on a 13 premiers points sommets d'une parastiche vert, le 14 (n°13) se retrouve dans le paratiche du premier point (n°0), le 15 eme est dans la suite du deuxième, et ainsi de suite.

Certes, mais celane dit pas pourquoi les nombres de Fibonacci dans le cas de l'angle d'or... Patience, j'y viens. Rappelons nous les angles rationnels, avec un angle p/q. Le q-ième point est aligné avec le point initial, et c'est le plus proche de ce premier point. Avec un angle irrationnel comme l'angle d'or, à présent : imaginons maintenant qu'il existe p et q tel que p/q s'approche de cet angle. Dans ce cas là, le q-ième point sera presque aligné avec le point initial, mais pas exactement. Le décalage forme alors le parastiche.
Mais combien vaut l'angle d'or, déjà ? 360*1/ ! On cherche donc p et q tels que p/q = 1/, et ces nombres, on les connais, puique je l'ai expliqué dans la dernière note : ce sont des nombres de la suite de Fibonacci ! (2,3), (3, 5), (5, 8) ou (8, 13)... Évidemment, c'est un modèle, qui diffère suivant la vitesse de croissance de nos amies les plantes et d'autres traits de caractères inhérents à la vie de toute plante.

CQFDJC ! (Ce qu'il fallait démontrer, je crois)

Bon, tout ça explique beaucoup de chose, mais pourquoi donc l'angle d'or, alors que n'importe lequel aurait tout à fait fait l'affaire ? Et bien, celà s'explique très bien, mais ça rentre dans un domaine encore plus biologique, une sombre histoire de lumière disponible et de croissance de primordia au niveau de l'apex... Quelques informations ici pour les fans de bio-mathématiques !
Et sinon, la grande majorité des illustrations a été piquée ici (Sur ce lien, vous pourrez découvrir comment enseigner ceci à des primaires, avec expériences à l'appui, exercice fort amusant)

Ffiou, trois notes pour en arriver là !...

Comments

[El Jj]

Phoenixx > Moi, ce que j'en dit, c'est la thèse extraterrestre...

(Et sinon, tu as raison, il y a eu cafouillage dans l'angle du schéma bleu)

[Phoenixx]

C'est vraiment vachement intéressant tout ça ... Et en plus, le pire c'est que ça a l'air vrai ! Rien à dire sur cette note, je vais rester en monologue avec moi-même pour essayer de déterminer d'où vient l'anomalie de mon ananas ...

PS : Pour le schéma bleu, t'aurais pas plutôt fait un angle de 4/7*360° ?

[Tipierre]

Bon sang mais c'est bien sur !