Attention à Attention à la marche

Cette fois-ci, c'est le ponpon, TF1 a dépassé les bornes. Je ne parle pas des propos de Le Lay sur le coca, ni des trucages des votes de la starac, ni de leur journeaux tendancieux, ni du nombre croissant d'émissions prenant les télespectateurs pour des imbéciles, mais d'une des questions dans "Attention à la marche" diffusé aujourd'hui même. La question était quelque chose comme ça :
"Si neuf invités sont réunis lors de la soirée du réveillon et que chaque invité trinque avec chaque autre invité, combien va t'on entendre de "tchin tchin" ?"
La réponse est 36, et pourtant, la réponse donnée par Jen-Luc Reichmann était 72...

Je veux bien que les combinaisons soient au programme de Terminale S, et donc, au dessus du niveau de TF1, mis quand même...

Afin de rendre TF1 meilleur, voici donc comment on peut trouver la bonne solution.
La soirée compte 9 invités. Chaque invité va donc bien trinquer avec 8 autres. On en conclut alors 9×8=72 trinquages... Erreur ! Si Albert trinque avec Bertrand, Bertrand va donc en même temps trinquer avec Albert.  En comptant 9×8, on va compter deux fois chaque trinquages.
La bonne réponse est donc 9×8/2=36.
On peut résumer dans un tableau, avec Albert, Bertrand, Christophe, Dominique, Émilie, Fannie, Gustave, Herbert et Isidore.

Je vous laisse compter, vous verrez que j'ai raison ! A bas TF1 !

Et sinon, pour ceux qui ont passé la terminale S, le problème, c'est de connaître le nombre de manières de prendre deux personnes parmi 9. Pour ceux qui ne se souviennent pas, la formule de k parmi n, c'est :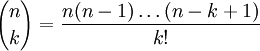

Ce qui donne finalement :

Et là, on retrouve encore 36 !
(Et on peut aussi trouver la réponse en faisant 1+2+...+n, donné par n(n+1)/2, avec n=8...)

Bref, la réponse, c'est 36, et c'estpour cette raison qu'il faut boycotter TF1 ! (On a déjà laissé passé 1 comme étant le premier nombre premier dans le maillon faible, là, c'était la goutte d'eau qui a fait déborder les toilettes !)

Et bonne année N à tous, avec N correspondant à l'année courante.

Comments

[Tût-tûûût]

Eh, du calme Nanick, personne n'est trop nul ici sauf TF1 : si les deux personnes disent Tchin-Tchin, ça fait 2 Tchin-Tchin et 4 Tchin, voilà tout.

Ceci dit, en Alsace on dit "Tchin-Tchin" et la personne en face répond "Tchin-Tchin" aussi.

Sinon à qui veut gagner des millions, y'a 50% du public qui pense que le soleil tourne autour de la terre...

[Nanick]

Franchement vous etes vraiment trop nul !
je comprend pas pkoi vous diviser par 2
Puisque je suis d'accord que si
pierre trinque avec philippe,
philippe trinque avec pierre
Mais les 2 personnes disent "Tchin Tchin"
donc on en entend 4 quand meme !

[Philippe]

Brillante démonstration :)

(Et, là, Le Lay se dit que les émissions ne permettent plus de vendre de Coca si les gens se mettent à réfléchir et à prouver que les informations sont erronées :))

[Abricot]

C'est idiot, il n'y en aurait même eut aucun si les invités avaient trinqués avec des gobelets en plastique !

[Mylou]

bon on est le 31 décembre, il est 22h 51 donc m'en voulez pas trop mais si chacun dit un seul tchin et donc que c'est la reunion des deux qu'on comptabilise ça fait pas plutot 18 ? ah ben nan en fait ça fait bien 36 quand on en fait qu'un mais ça fait bien 72 quand chacun dit tchin tchin parce que les deux le dise donc à chaque rencontre de verre on a bien 4 tchin et à ce moment dans ton tableau tu n'as que l'horizontale vers le verticale mais la verticale va le dire à l'horizontale donc il faut bien remplir 9 * 9 = 81 - 9 (parce qu'on trinque pas avec soi meme) donc 72 cases! non?(oui ça fait mal quand je fais des maths...)ceci étant dit la question était mal posée^^