Königsberg et les parcours eulériens
Dans cette intéressante excursion au milieu de la théorie des graphes, nous allons aujourd'hui rejoindre la belle ville de Königsberg, aujourd'hui Kaliningrad, située dans l'enclave de Kaliningrad (le bout de la Russie perdu entre la Pologne et Lituanie)

Cette belle ville de Könisberg est une sorte de Mecque pour tous les mathématiciens, puisqu'elle a donné naissance au célèbre problème de la théorie des graphes, celui des "sept ponts de Könisberg".
Comme le nom du problème semble l'indiquer, Könisberg possède sept ponts. Une photographie de l'époque le montre bien :
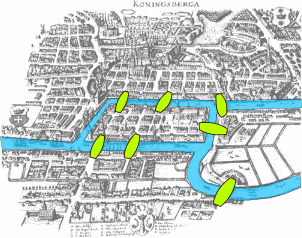
Le problème dans cette ville est celui de la visite touristique : comment passer par tous les ponts de la ville sans passer deux fois par le même (ou revenir en arrière sur un pont) et revenir au point de départ. Autant le dire tout de suite, ce n'est pas possible...
En termes plus mathématiques, il faut trouver un cycle eulérien dans le graphe représentant la ville. Le graphe de la ville est ci-dessous : les arrêtes (lignes) représentent les ponts et les sommets (les cercles) représentent les îlots ou le continent. Un cycle eulérien, c'est un chemin qui passe une unique fois par toutes les arrêtes et qui revient à son point de départ. (Une chaîne eulérienne, c'est comme un cycle, mais il n'y a pas besoin de retourner au point de départ)

Tout le monde (j'espère) connait ce célèbre jeu qui consiste à tracer une sorte de maison (ou n'importe quel autre dessin) "sans lever le crayon". Il s'agit ni plus ni moins que de retrouver une chaîne eulérienne dans le graphe suivant...
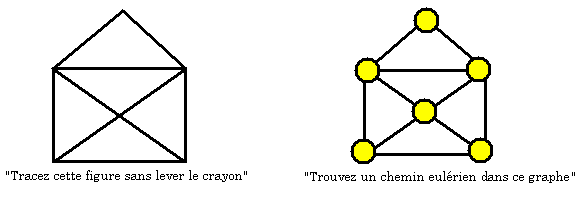
Et comme ce blog a une volonté tout à fait pédagogique, même sur des problèmes de "tracé de figures sans lever le crayon", il faut savoir qu'il y a un truc à connaitre : pour qu'un tracé soit faisable sans lever le crayon (pour qu'il existe une chaîne eulérienne dans un graphe), il faut que le nombre de sommets possédant un nombre impair d'arêtes soit de zéro ou de deux. Il faut également savoir que l'on commence toujours et termine toujours en ces sommets.
Si on veut trouver un cycle, il faut qu'il n'y ait que des sommets avec un nombre pair d'arêtes...
A ne pas confondre avec les chaînes hamiltoniens (cf dernière note) dans lesquels il s'agit de trouver un chemin passant par tous les sommets de manière unique.
Et tant qu'on parle des graphes, on va continuer la prochaine fois avec le métier qui terrifie les mathématiciens et informaticiens : les voyageurs de commerce.
Sources :
Un peu de wikipédia (pour les jolies illustrations, les moins jolies sont de mon cru)



/http%3A%2F%2Fstorage.canalblog.com%2F72%2F92%2F210892%2F113119539_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F00%2F91%2F210892%2F107069165_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F33%2F48%2F210892%2F101190494_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F83%2F38%2F210892%2F101168363_o.png)