Mon papa, il est mille fois plus fort que le tien !
- Mon papa, il est plus fort que le tien !
- Nan, c'est le mien le plus fort !
- C'est pas vrai, parce que le mien, il est 100 fois plus fort !
- Nan, le mien, il est un million de fois plus fort !
- Mais le mien, il est un millions plus une fois plus fort !
Bon, évidemment, à moins de s'essouffler, on peut continuer cette discussion intéressante indéfiniment, tant qu'on arrive à trouver des nombres toujours plus grand... Alors, comment mettre K.O. son adversaire au jeu du "Mon papa, c'est le plus fort" ? Tel est l'objet de cet article !
Pour atteindre des grands nombres, rien ne vaut les puissances de 10, c'est d'ailleurs comme ça que commencent toute bonne partie de "mon papa, c'est l'plus fort". Les choses risquent fort de commencer comme ça, les plus simples des grands nombres :
Cent (100), Mille (1 000) , un million (1 000 000), un milliard (1 000 000 000), etc.
Et après ?
Le débat fait rage, puisque deux écoles s'affrontent. D'un côté, ceux qui adoptent la progression par 1000 et ceux qui adoptent la progression par 1 000 000, ce qui rend les discussions à propos de grands nombres incompréhensibles (d'où l'utilisation des puissances de 10).
Selon la règle traditionnelle, on a ensuite le trillion (1012), le quatrillion (1015), le quintillion (1018), le sextillion (1021), le septillion (1024), l'octillion (1027) etc.
Selon la règle officielle, on a ensuite le billion (1012), trillion (1018), le quatrillion (1024), le quintillion (1030), le sextillion (1036), le septillion (1042), l'octillion (1048) etc.
Il y a encore d'autres systèmes utilisés, mais on va rester sur le système officiel.
Mais tout ça, finalement, ça reste des petits nombres, on peut aller bien plus loin. Archimède, par exemple, en s'amusant à compter les grains de sables, a supposé que la sphère terrestre pouvait contenir 1064 grains de sable... Carl Sagan, quant a lui, a estimé le nombre d'atomes dans l'Univers a 1080.
Et après ?
On peut toujours trouver des nombres plus grands ! Leur gros problème résidera dans le fait qu'il ne représentent pas grand chose de physique.
C'est histoire de créer des grands nombres que Kasner demanda à son neveu un nom pour le nombre qu'il venait d'inventer, 10100 (utilisé pour parler d'un nombre grand qui n'est pas l'infini). Alors âgé de 8 ans, son neveu lui répondit "gogol". C'est ainsi que le gogol fut né, un "un" suivit de cent "zéros". C'est d'ailleurs de là que vient le nom du moteur de recherche, qui, à terme, devrait recenser un gogol de pages... Ce nombre reste malgré tout à peu près égal à 70! (factorielle de 70, c'est à dire, 1×2×3×...×70).
Et après ?
On a le nombre de Shannon (10120), c'est à dire, le nombre théorique possible de parties d'échec !
Et après ?
Et bien, c'est à ce moment là qu'il faut citer l'asaṃkhyeya (असंख्येय, pour les grammar nazi du sanskrit), qui vaut environ 10140, qui est un nombre bouddhiste, littéralement "au dela des nombres". C'est le nombre considéré comme étant le plus grand. En effet, un bouddhiste jouant au jeu du "Mon papa c'est l'plus fort" ne pourra pas aller plus loin que "Mon papa est un Asaṃkhyeya de fois plus fort que toi"... La valeur de l'asaṃkhyeya reste cependant sujette à caution, puisqu'il vaut 105×2^103 ou 107×2^103 (un nombre possédant environ 1032 chiffres.
Et après ?
Mais ces nombres sont ridiculement petits par rapport à ce qui suit : les plex ! Dans la foulée du gogol fut inventé le gogolplex, égal à 10un gogol. (D'où le nom du siège social de google, le googleplex). D'autres mathématiciens ont prolongé le concept, un disant qu'un N-plex valait 10N, et donc, le gogolplexplex vaut 10un gogolplex.
Et après ?
Et bien, c'est là que Knuth arrive et propose un tout nouveau système de puissance.
Avant, nous avions l'écriture ab, que l'on comprenait comme ça :

Et bien, Knuth propose un système de doubles flèches verticales :

On a, par exemple, ![]()
ou ![]() , nombre considérablement plus grand que le gogolplex.
, nombre considérablement plus grand que le gogolplex.
Et après ?
Et bien, Knuth a encore agrandi son concept de flèches, en proposant la triple flèche, la quadruple flèche et la n-flèche définie de manière récursive. Ca donne alors quelque chose comme ça :
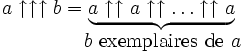
On a, par exemple, ![]()
Et en généralisant, ça donne :

Ces nombres ont eu une application concrète, celle du nombre de Graham, le plus grand nombre jamais utilisé dans une démonstration mathématique (une sombre histoire de coloration d'hypercube), qui correspond au 64e terme de cette suite :
u1 = 4
u2 = ![]() (Avec 4 flèches)
(Avec 4 flèches)
u3 = ![]() (Avec u2 flèches)
(Avec u2 flèches)
Et ainsi de suite jusqu'à u64, le nombre de Graham, qui aura u63 flèches...
Et après ?
Et bien à ce niveau là, on se dit que les nombres deviennent trop grand (ce qui n'est pas peu dire...) et qu'il serait inutile d'en chercher des encore plus grand... Et pourtant, il existe une notation permettant d'en avoir des encore plus grands ! C'est la notation des flèches de Conway (toujours lui !).
Dans cette notation, les nombres s'écrivent sous la forme d'une chaîne, comme 2 → 15 → 42 → 7. Dans ce cas là, la chaîne est de longueur 4, composé d'une chaîne queue (2 → 15 → 42) et d'un terme de tête (7).
La valeur numérique de cette chaîne est définie de manière récursive de façon plutôt compliquée, mais qui permet de fabriquer des nombres particulièremnt grands :
-
Une chaîne de longueur 1 représente le nombre.
-
Si la chaîne est de longueur 2, c'est l'exponentiation classique : p → q = p<sup>q</sup>
-
Si l’un des terme de la chaîne vaut 1, la chaîne est coupée, et on ne conserve que sa première partie.(c’est la seule façon de réduire la taille d’une chaîne) : pour X et Y des sous-parties de la chaîne, on a Y → 1 = Y et Y → 1 → X = Y.
-
Si la chaîne est de longueur supérieure ou égale à 3, elle est égale à une chaîne de même longueur où le nombre de tête est décrémenté, et où l'avant-dernier terme est considérablement plus grand (ce terme est égal à la chaîne, et où l’avant dernier terme est décrémenté de 1) :
Y → p → q = Y → (Y → (p-1) → q) → (q-1) (pour p,q ≥ 2)
Ainsi, la chaîne 2 → 15 → 42 → 3 est égale à 2 → 15 → (2 → 15 → 41 → 7) → 2 (chaîne de longueur 4, avec un terme de tête plus petit, mais avec un avant-dernier terme vraiment énorme). En appliquant la règle de récursion encore une fois, on obtient :
2 → 15 → (2 → 15 → (2 → 15 → 41 → 7) → 2) - 1 → 1.
Puisque le dernier terme est 1, on peut raccourcir la chaîne, qui devient de longueur 2. Le soucis, c’est que son dernier terme est maintenant (2 → 15 → (2 → 15 → 41 → 7) → 2) - 1, un nombre grand. Très grand. Immensément grand. Inimiginablement grand… Du coup, le nombre d’étapes nécéssaire pour diminuer à 2 la longueur de la chaîne dépasse l’entendement.
Cette notation permet de donner un encadrement du nombre de Graham, qui simplifie un peu sa définition :
3 → 3 → 64 → 2 < G < 3 → 3 → 65 → 2
Mais ce nombre de Graham reste tout de même ridiculement petit par rapport au nombre 3→3→3→3 ...
Et après ?
On pourrait toujours s'amuser à définir une notation correspondant à des itérations de notation des flèches de Conway, mais pour l'instant, aucun mathématicien n'a jugé utile de le faire...
- Mon papa, il est plus fort que le tien !
- Nan, c'est le mien le plus fort !
- C'est pas vrai, parce que le mien, il est 100 fois plus fort !
- Nan, le mien, il est factoriel de l'itération d'un nombre de Graham de fois de la notation en flèche de Conway avec le gogolplex...plex avec un Asaṃkhyeya de "plex" de fois plus fort que ton père !!!!
- Euh... et ben... euh... Le mien, il est factoriel de l'itération d'un nombre de Graham de fois de la notation en flèche de Conway avec le gogolplex...plex avec un Asaṃkhyeya de "plex" plus une fois plus fort !
Sources :
Les grands nombres
Notation des puissances itérés de Knuth
Notation des flèches chaînées de Conway



/http%3A%2F%2Fstorage.canalblog.com%2F17%2F83%2F210892%2F102674861_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F59%2F97%2F210892%2F93981751_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F53%2F54%2F210892%2F92246854_o.png)
/http%3A%2F%2Fi17.servimg.com%2Fu%2Ff17%2F11%2F01%2F08%2F23%2Fcanvas10.png)