La formule de Marcel Pagnol

Marcel Pagnol : 28 février 1895 - 18 avril 1974. Écrivain, dramaturge, cinéaste et académicien français, on lui doit entre autre ses souvenirs d'enfance... Mais pas seulement ça ! On lui doit aussi ceci :

Si n est impair, alors n+(n+1)+n(n+1) est premier.

Pour n=1, 1+2+1×2=5 (premier)
Pour n=3, 3+4+3×4=19 (premier)
Pour n=5, 5+6+5×6=41 (premier)
etc.
Bon, évidemment, si il avait essayé n=11, il aurait vu que 11+12+11×12=155, qui n'est pas un nombre premier (Divisible par 5).

Un formule qui donnerait tous les nombres premiers, ça serait quelque chose de beau, non ?! Ca pourrait permettre d'avoir des nombres premiers aussi grands que l'on veut. Aujourd'hui, on ne connait pas de nombres premiers plus grands que 2^32582657+1...

Après tout, il y a bien une formule qui donne tous les nombres impairs (2n+1) ou une qui donne tous les nombres de Fibonacci (), alors pourquoi pas une formule qui donnerait tous les nombres premiers ?

Pagnol n'est pas le premier à s'y être cassé les dents avec sa formule (4n²+10n+5), Euler a été le premier à s'y atteler. A l'époque, il a trouvé la formule n² − n + 41... (Qui, évidemment, ne marche pas pour n=41, car le résultat sera divisible par 41). On a fini par démontrer qu'on ne pouvait pas trouver de polynôme a une seule variable donnant tous les nombres premiers.

Si cette formule existait, ça se saurait : on l'aurait depuis longtemps utilisé pour battre ce misérable record du nombre premier le plus grand (9 808 358 chiffres).

Et pourtant ! Il y a bien un polynôme qui donne la totalité des nombres premiers. On doit cette formule à Jones, Sato, Wada et Wiens en 1976. Voici la formule :

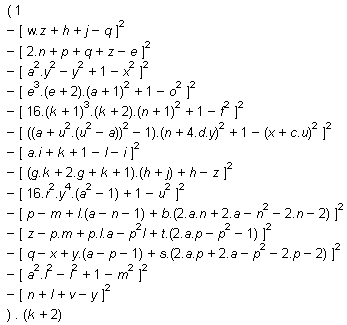
C'est vrai, on a déjà vu des formules plus simples, mais celle-ci fonctionne, elle peut donner tous les nombres premiers, pourvu que le résultat est positif. C'est simplement un polynôme de degré 25 avec 26 variables.

Evidemment, il y a un hic, quand on regarde de plus près la formule. Il s'agit du produit de deux membres : d'un côté, (k+2), et de l'autre, (1-plein de choses). Pour obtenir un résultat positif, il faut nécéssairement que le "plein de chose" soit nul : il s'agit finalement d'un système de 14 équations diophantiennes (à coefficients entiers) à 26 inconnues. Autant le dire simplement : c'est quasiment impossible d'avoir de solutions avec cette formule. A l'heure d'aujourd'hui, on a juste réussit à obtenir 2...

Mais ce n'est pas grave ! Lâchons les polynomes (même s'il y en a d'autres du même genre, dont un avec 10 variables, de de degré 1045) et cherchons une autre formule qui pourrait donner tous les nombres premiers.

Grace au théorème de Wilson (une histoire de congruence sur les nombres premiers), on a pu trouver une très chouette formule, qui donne tous les nombres premiers dans l'ordre :

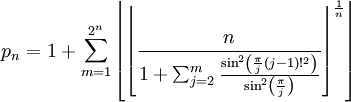
(Les drôles de traits verticaux, c'est la fonction partie entière)

Sinon, si vous n'aimez pas les sinus et les factoriels, il y a aussi cette charmante formule plutôt basée sur les parties entières...

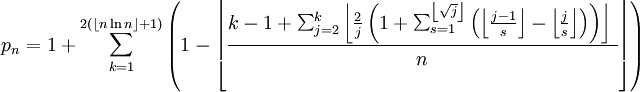
En fait, ces deux formules sont aussi inutilisables que la formule de Jones, Sato, Wada et Wiens, on a plus vite fait de prendre des nombres au hasard et de tester leur primalité par des algorithmes simples.

Tous ça pour dire que l'on cherche encore la formule miracle...
Si elle existe...

---

Sources :
Fortement inspiré de wikipédia
(Et un peu d'une conférence donnée à la fac sur le sujet)

Comments

[djmadman]

Après tout, il y a bien une formule qui donne tous les nombres impairs (2n+1)



voilà ce que j'ai retenu :p (qui est logique) après le reste ça risque de me donner des mots de tête mais intéréssent tout de même

[bencha]

arf, message tronqué, le double < ne passe pas.

donc, pour m < et < n (j'ai encore du mal à trouver une limite), on peut commencer la formule par p(n)= m + S de k=m à ...

Merci pour ce blog passionnant.

[bencha]

Merci. Ruby fait de même avec les intervalles, donc ça marche^^

Sinon, je trouve cette formule très bien, pas pour le calcul force brute, c'est lent, mais si on cherche à calculer les nombres premiers successifs, le dividende au dessus du /n ne dépend que de k, donc on peut les garder en conserve, et même utiliser le dernier pour calculer le suivant. Si on ajoute que pour m< les étudiants vont pouvoir s'amuser à apprendre à remplir des listes d'un coté en les vidant de l'autre, ça les changera du crible d'Ératosthène.

[El Jj]

bencha > On zappe ! En général, on accompagne la formule d'une petite phrase qui précise ce qu'il se passe dans ce genre de cas particuliers, ce que je n'ai pas fait...

[bencha]

Bonjour,
Article intéressant, jolies formules, j'essaie la dernière, celle à valeurs entières, mais pour le moment je n'obtiens que les 2 premières valeurs justes. Outre les bugs éventuels que je chasse, ça donne quoi en maths une somme de j=2 à k pour k=1 ? On compte à rebours ou on zappe ?