Farey, Ford et les autres

- Dis, Jj, c'est quoi ton avatar MSN ?
- ...
- Jj, c'est quoi ton avatar MSN ?
- ...
- Jj, c'est quoi l'hypothèse de Riemann ?
- Et bien, mon avatar MSN, c'est l'adaptation des cercles de Ford aux fractions complexes... Quelques explications sont nécessaires, semble t'il...

Sir John Farey

Farey, géologue-mathématicien-écrivain anglais de son état, n'a pas vraiment découvert les suites de Farey portant aujourd'hui son nom, il a simplement fait quelques conjectures à son propos, mais Cauchy qui passait par là lui a donné tout le mérite.

Bref, une suite de Farey (d'ordre n), qu'est ce que c'est ? En termes simples, ce sont toutes les fractions irréductibles entre 0 et 1 que l'on peut écrire avec des nombres entre 0 et n.

Par exemple, on a
F₃ = {⁰⁄₁, ¹⁄₃, ¹⁄₂, ²⁄₃, ¹⁄₁}
F₄ = {⁰⁄₁, ¹⁄₄, ¹⁄₃, ¹⁄₂, ²⁄₃, ³⁄₄, ¹⁄₁}
etc.

Quelques propriétés intéressantes :

* Quand on prend deux termes consécutifs de la forme ^a⁄_b < ^c⁄_d, on a toujours bc-ad=1

* Quand on prend trois termes consécutifs de la forme ^a⁄_b < ^p⁄_q < ^c⁄_d, on trouve que ^p⁄_q est le médian de ^a⁄_b et de ^c⁄_d :

C'est d'ailleurs cette deuxième propriété que John Farey n'a jamais su démontrer.

Lester Ford (père)

Mais les suites de Farey sont très jolies, mais il leur manque un petit quelque chose : une représentation graphique. C'est là que Ford, mathématicien américain, arrive, et propose de représenter chaque fraction par un cercle, que l'on appellera "cercle de Ford".

Le cercle associé à une fraction p/q irréductible, c'est le cercle de centre (p/q, 1/2q²) et de rayon 1/(2q²).

On peut alors représenter les différentes suites de Farey avec ces cercle de Ford.
Ainsi, la suite F₇ se représente ainsi (J'ai omis de représenter les cercles correspondant à 0/1 et 1/1, ils sont trop gros):

Et le plus étonnant dans tout ça, c'est que chaque cercle est tangent à son voisin ! On peut toujours aller plus loin, et représenter la suite de Farey à l'infini, ce qui donne une très jolie fractale. Chaque cercle embrasse alors une infinité d'autres cercles. :

   

Clifford A. Pickover
Et c'est là que Pickover, chroniquer scientifique et inventeur des nombres vampires, arrive, et propose de remplacer les cercles par des sphères.

Mais comme ça n'apportait pas grand chose, il s'est dit qu'il serait intéressant d'adapter les fractions des suites de Farey en fractions complexes (Si vous ne connaissez rien aux complexes, cette partie là sera encore plus difficile à suivre)

Maintenant, au lieu de prendre toutes les fractions irréductibles de la forme p/q, on prend toutes celles de la forme (p'+ip")/(q'+iq") (p', p", q' et q" sont tous entiers). Un petit calcul permet de trouver que cette fraction est de la forme a+ib, avec a et b étant des fractions réelles.
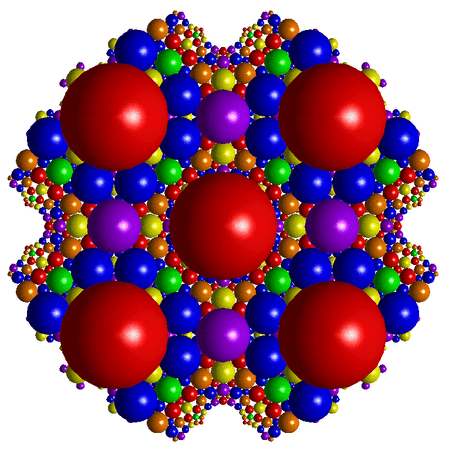
Ensuite, il n'y a plus qu'à les représenter dans le plan complexe avec des sphères de la même façon que pour les cercles de Ford.
Pour une fraction complexe p/q, on lui associera la sphère de rayon 1/(2qq) (q étant le conjugué de q) et touchant le plan complexe à la position p/q. Une fois que l'on a fait tout ça avec un ordinateur disposant de bons logiciels, on trouve ceci :

Et c'est à ce moment là que l'on peut se dire que même si on peut trouver que tout ça ne sert à rien, c'est quand même très joli !

(Mais en vrai, les suites de Farey ont une importance dans le problème de l'hypothèse de Riemann, problème du prix du millénaire à un millions de dollars)

---

Sources :
Le baiser infini (d'où proviennent la plupart des images de cet article)
Wikipédia (On ne change pas une équipe qui gagne)

Comments

[Fara]

Bien mais pas bien clair

[Whiteshoulders]

xpldrasfptlv6 le debut de la note !
Tres joliement expliqué tout ça ... ça m'aide pour les "petites" revisions que j'ai a faire pendant les "vacances".

[abab]

Le superdupont d'abab lui suffit, merci. Ou à la rigueur capitaine Flam. Mais suremement pas une equation du 6e degré, ce n'est pas très romantique.

[Tipierre]

C'est presque aussi mignon qu'un chaton ! J'adore l'intro de la note !

[Zetron]

C'est beau.