Les courbes monstres
Elles sont apparues au XIXe siècle, et ont été loin de laisser indifférent : Poincaré les a qualifiées de "monstres" et Hermite de "plaies lamentables". On les appelle plus affectueusement "pathologiques"... Mettons-les pour une fois à l'honneur !
Une courbe continue : une courbe que l'on peut tracer sans lever le crayon.
Si le mouvement de la main est soyeux et délicat (le crayon ne s'arrête pas, ne trace pas d'angles), on dit que la courbe est dérivable (enfin, on dit plutôt que la fonction est différentiable, mais on est pas à cette approximation près...).
Les courbes les plus simples que l'on imagine sont continues et dérivables, mais il arrive, même dans la vie d'un lycéen, que la courbe de la fonction ne soit plus dérivable en un point précis. La courbe y est alors anguleuse, et n'y admet pas de tangente. L'exemple le plus simple est le graphe de la fonction valeur absolue :
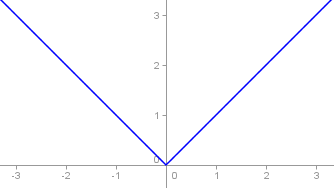
Graphe de la fonction f(x)=|x|
Fonction continue et dérivable sauf en 0
Cette fonction a le mérite d'être continue (la courbe peut sans problème être tracé sans lever le crayon), mais n'est pas dérivable en 0 (la courbe y est anguleuse, le mouvement de la main pour tracer la fonction ne sera pas velouteux). Heureusement, partout ailleurs, la courbe est bien dérivable (On dit qu'elle est dérivable presque partout)
On peut alors facilement s'imaginer des courbes continues qui ne sont pas dérivables partout : on appelle ça des zig-zag !
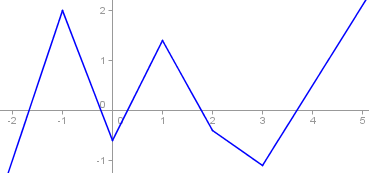
Graphe d'une fonction zigzag
Fonction continue mais non dérivable en -1, 0, 1, 2 et 3
Cette fonction reste tout de même dérivable presque partout : il n'y a que 6 points où elle ne l'est pas (les points anguleux), ce qui est négligeable vu le nombre de points où elle l'est. On peut même imaginer une fonction continue mais non dérivable en une infinité de points (un zig-zag infini), mais l'ensemble des points où la fonction n'est pas dérivable reste négligeable !
Ce genre de choses était déjà bien connu à la fin du XVIIIe siècle (où les problèmes étaient généralement de trouver la dérivée d'une fonction donnée), et on s'est rapidement dit que toutes les courbes continues devaient n'avoir qu'un nombre négligeable de points anguleux. Une courbe partout continue et nulle part dérivable : inimaginable !
André-Marie Ampère (celui qui a donné son nom à l'unité électrique) a même tenté de démontrer en 1804 que toute courbe ne devait avoir qu'un nombre négligeable de points de non-dérivabilité. Aujourd'hui, on a toujours du mal à comprendre ce qu'il a voulu prouver, et de toutes façons, il avait tord !
La courbe de Bolzano
La toute première courbe partout continue et nulle part dérivable (On va appeler ça une courbe ND) est l'œuvre du mathématicien tchèque Bernard Bolzano, découverte en 1830. Il faudra tout de même attendre 1930 avant qu'elle ne soit publiée. Par sa construction, on peut l'identifier comme étant la première fractale de l'histoire ! Elle ressemble à ceci :
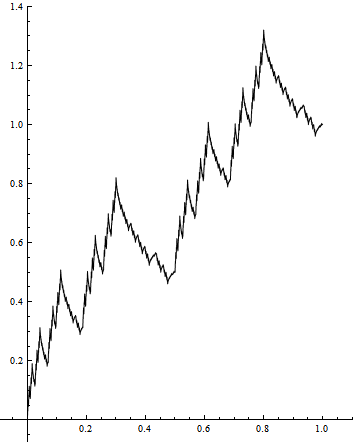
Courbe de Bolzano
(Continue partout, dérivable nulle part)
Pour la construire, on part de deux points A(0,0) et B(1,1). (On a le segment B0=[AB]). Pour obtenir B1, on construit les trois nouveaux points suivants : C(3/8,5/8), D(1/2,1/2) et E(7/8,9/8). La courbe B1 est le zigzag ACDEB. Pour passer à B2, il faut reprendre chaque segment composant B1, et les transformer en zigzag selon l'opération décrite à l'étape précédente. En itérant ce processus une infinité de fois, on obtient la courbe de Bolzano. Les trois premières étapes sont représentées ci-dessous :
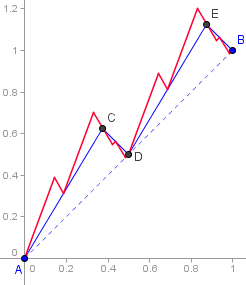
En pointillé, B0 ; en bleu B1 ; en rouge B2
Cette courbe est ND : elle est continue (ce ne sont que des bouts de segments), mais dérivable nulle part (tout point est un angle)
Les courbes de Weierstrass
La star des courbes ND, c'est bien celle-ci ! Le 18 juillet 1872, le mathématicien Karl Weierstrass présente devant une foule médusée non pas une, toute une famille entière de fonctions continues dérivables nulle part ! Il en existait bien deux autres alors, mais n'étaient pas publiées (celle de Bolzano et celle de Cellérier, qui est un cas particulier de celle de Weierstrass).
Les courbes de Weierstrass sont données par la formule suivante :
Pour 0 < a < 1 et b impair donnés tels que ab>5,72 (On a prouvé bien plus tard que ab>1 suffit)
Prenons par exemple a=1/3 et b=5. On a alors :
W(x) = cos(πx) + cos(5πx)/3 + cos(25πx)/9 + ...
Autrement dit, une somme de fonctions cosinus (toutes aussi continues et dérivables les unes que les autres, mais de plus en plus sinueuses et tassées), ce qui donne :
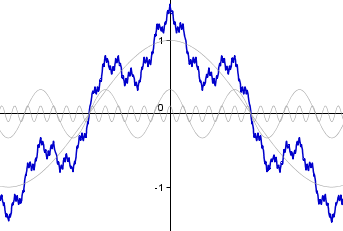
Fonction de Weierstrass
En gris les sinusoïdes à sommer pour obtenir la fonction
Bref : dérivable + dérivable + dérivable +... = non dérivable !
La courbe du blanc-manger
Une petite dernière, datant de 1903 : la courbe de Tagaki, alias courbe du blanc-manger (parce qu'elle ressemblerait au blanc-manger, un pouding au lait d'amande. On y ajoute de la noix de coco, de l'abricot ou des fruits rouges, selon les préférences culinaires).
Elle est bâtie sur le même principe que la courbe de Weierstrass : une somme de fonctions de plus en plus oscillantes (mais non dérivables pour cette fois). Sa formule est la suivante :
Elle consiste donc en la somme de fonctions en montagnes. En rouge, pour k=1, en jaune, pour k=2 etc.
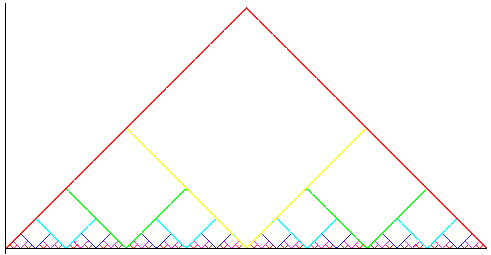
Courbes à sommer pour obtenir la courbe de blanc-manger :
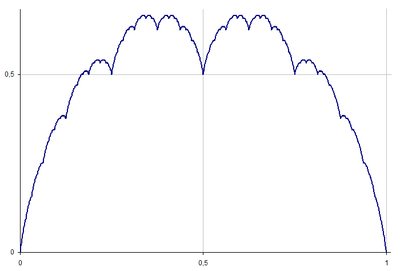
La courbe de Tagaki
L'année suivante, Koch construisait son célèbre flocon, lui aussi continu partout et dérivable nulle part... On a dernièrement découvert une famille de fonctions à base de produits infinis (Les fonctions de Wen, en 2002) !
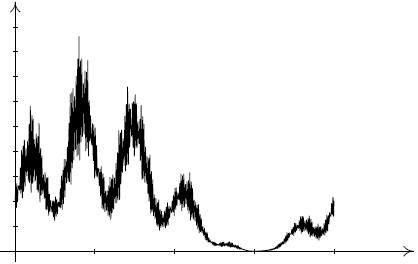
Fonction de Wen
Continuous Nowhere Differentiable Functions - Thèse de Johan This
Recette du blanc-manger