Le jeu de l'interpolation Lagrangienne
Un polynôme est, d'après mon Larousse 1991, une "somme algébrique de monômes", un monôme étant, selon le même dictionnaire, une "expression algébrique formée d'un seul terme"... Bref, mon dictionnaire ne sait pas ce qu'est un polynôme, mais cherche à nous embrouiller dans un jargon approximatif.
Un polynôme (pour simplifier, à une inconnue, à coefficients réels) est quelque chose qui ressemble à ça :
42.X8 + 5π.X3 - 2.X + 1
(Polynôme d'indéterminée X)
Formellement, un polynôme (de degré n) est une expression qui peut s'écrire sous la forme :
an Xn + an-1 Xn-1 + ... + a1X + a0
(Ou les an, an-1, ..., a0 sont des nombres (réels) )
Quand on est chichiteux, on distingue le polynôme (une expression algébrique, comme au-dessus), de la fonction polynomiale (qui a x associe l'évaluation de ce polynôme en x). On ne peut pas forcément identifier l'un avec l'autre, mais on va faire comme si, ça va nous simplifier les choses.
L'une des raisons d'être des maths au collège est la manipulation des polynômes : on les factorise, on les développe, on en cherche des racines. Il arrive même de les dériver ou de les intégrer, ce qui est plus facile à faire pour des fonctions polynomiales que pour des fonctions quelconques.
Mais au fait... Pourquoi nous avoir appris tout ça au lycée ? Aujourd'hui semble donc un grand jour pour donner quelques grandes idées de la raison d'être des polynômes en analyse numérique : l'interpolation et la quadrature des fonctions.
Interpolation de Lagrange
Prenons N points d'un intervalle [a,b].... Euh...
Disons plutôt, (pour simplifier) prenons les 3 points suivants : x0=0, x1=1 et x2=2, et considérons les trois polynômes suivants (appelés "polynômes de Lagrange"):


Représentation graphique de L0, L1 et L2
Prenons par exemple L0(X) : évalué en X=1 ou X=2, il donne 0, et évalué en X=0, il donne 1.
De la même façon, on a Lj(xi)= 0 si i≠j, et 1 si i=j.
Considérons maintenant le polynôme Pabc(X) = a.L0(X)+b.L1(X)+c.L2(X) (avec a, b et c des nombres de votre choix).
D'après ce que l'on a vu juste au-dessus, on peut maintenant dire que Pabc(0)=a, Pabc( 1)=b et Pabc(2)=c.
Imaginons maintenant un problème physique dans lequel apparaît une fonction f dont l'expression est bien compliquée, du genre de celle que l'on a pas du tout envie de calculer... On demande de tracer le graphe de cette fonction sur l'intervalle [0,2]... La démarche classique qui consiste à calculer la valeur de la fonction en tout un tas de points est impossible ici, puisque l'expression est vraiment trop compliquée (ce qui demanderait, même à un ordinateur, beaucoup trop de calculs)
Pas de panique ! Les polynômes de Lagrange sont là ! Au lieu de calculer la valeur de la fonction à tous les points de l'intervalle [0,2], on va calculer seulement les valeurs a=f(0), b=f(1) et c=f(2). On peut alors voir que le polynôme Pabc (que j'ai défini juste au-dessus) et la fonction f ont les mêmes valeurs en x=0, 1 et 2. Graphiquement, (et si certaines conditions, que je préfère taire, sont réunies) le polynôme et la fonction f seront très proches. Il suffira de dessiner Pabc (facile à dessiner, c'est un polynôme) au lieu de f, et l'on y verra que du feu...
Petit exemple, avec une fonction f terriblement compliquée, en jaune (J'ai pris f(x)=ex²/5... Ça aurait pu être pire...). On peut l'approcher (enfin, l'interpoler...), avec le polynôme Pabc. Graphiquement, les deux courbes sont plutôt proches.

Interpolation polynomiale en 3 points de f.
La courbe est encore mieux approchée quand on multiplie le nombre de points (en ajoutant, par exemple, les points 1/2 et 3/2). Après avoir recalculé les polynômes de Lagrange correspondant et les valeurs de f en 1/2 et 3/2, on trouve :
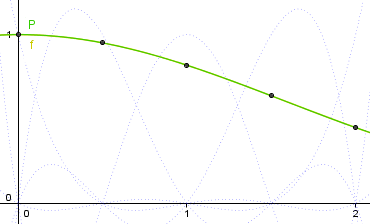
Bref, les polynômes servent ici à remplacer des fonctions trop compliquées par des fonctions plus simples : des polynômes !
Notons à ce point de l'exposé que, comme tout en maths, l'idée d'interpoler une fonction par des polynômes de cette façon est une idée de Leonhard Euler. (En fait, elle vient de Waring 4 ans plus tôt, mais on préfère retenir Euler)
[Ici, on vient "d'interpoler" la fonction f : on a trouvé un polynôme égal à f sur un certain nombre de points, en espérant qu'il soit proche sur tous les autres points.
On pourrait, en prenant les polynômes de Bernstein plutôt que ceux de Lagrange, véritablement "approcher" la fonction, en construisant un polynôme dont la courbe est partout proche de celle de f. Le résultat n'en sera que meilleur, mais la théorie derrière est plus difficile]
Quadrature de Simpson
L'intérêt esthétique de l'interpolation est là (parce que tracer des fonctions, cay cool), mais ce n'est pas le seul.
En physique (ou ailleurs), il arrive non seulement que l'on trouve des fonctions horribles, mais qu'il faille en plus en calculer l'intégrale (Plus concrètement, l'intégrale d'une fonction est son "aire sous la courbe"...).
Même avec des fonctions pas si compliquée que ça (du genre de la fonction f juste au-dessus), il est parfois impossible de connaître une expression de l'intégrale. Avec des fonctions compliquées, c'est évidemment encore pire. Faute d'une valeur exacte, une valeur approchée serait cependant tout à fait appréciable !
Mais puisque la courbe est approchable facilement par un polynôme, et qu'un polynôme, c'est facile à intégrer, cela donne un moyen parfait pour calculer des valeurs d'intégrales.
Prenons une fonction f quelconque (ou, du moins, suffisamment continue), sur l'intervalle [0,2]. On va appeler P le polynôme qui l'interpole en x=0,1 et 2. On a vu que P(x) = f(0).L0(x)+f(1).L1(x)+f(2).L2(x).
Quand on intègre notre fonction f, on va trouver ceci :

(première égalité : on approche f par P ; la deuxième égalité s'obtient par linéarité de l'intégrale : la dernière égalité consiste à calculer explicitement l'intégrale de L0, L1 et L2, ce qui est facile, puisque ce sont des polynômes)
Bref, grâce à l'interpolation, on a trouvé une formule pour l'intégrale sur [0,2] de f, qui vaut environ :
![]()
Cette simple formule (appelée formule de Simpson - de Thomas Simpson) permet de retrouver l'aire sous une courbe quelconque en ne connaissant sa valeur qu'en seulement 3 points équidistants (j'ai pris l'intervalle [0,2], mais on peut l'adapter à un intervalle [a,b] quelconque).
Évidemment, plus la courbe sera lisse, plus précise sera la valeur donnée par la formule...
[En prenant les points équidistants pour l'interpolation, on trouvera des formules d'intégration appelées "formules de Newton-Cotes". Plus on prend de points, plus précise sera la formule... (et plus difficile elle sera à mettre en pratique, où on s'arrête aux méthodes à 3 points) ]
Prenons par exemple la fonction f(x)=2/(1+x²/4). Par un heureux hasard, la valeur exacte de l'aire sous la courbe sur [0,2] de cette fonction est π. L'aire donnée par la formule de Simpson est 47/15, qui vaut environ 3.13. Deux décimales exactes, donc !

Dans la pratique (quand on veut vraiment calculer informatiquement des intégrales de fonctions plus ou moins compliquées), on préfère commencer par diviser en plusieurs sous-intervalles le grand intervalle sur lequel on veut intégrer, puis on applique la formule de Simpson sur ces sous-intervalles. Il y a plus de calculs à faire, mais le résultat est bien meilleur.
On pourrait même pousser le vice à changer les points que l'on prend dans l'interpolation (au lieu de les prendre équidistants, on pourrait les prendre autrement). En choisissant intelligemment les points (à travers des considérations sur l'orthogonalité de polynômes...), on peut faire en sorte que les formules que l'on obtient soient les meilleures possibles (on parle d'ordre d'une méthode, celle de Simspon est d'ordre 2, ce qui signifie qu'elle donnerait une valeur exacte pour n'importe quel polynôme de degré 2). On entre alors dans les méthodes d'intégration de Gauss-Legendre, les meilleures sur le marché de l'intégration (réellement utilisées en pratique par les analystes numériques)
Bref, l'une des raisons d'être des polynômes est de simplifier la vie des physiciens, en permettant de calculer efficacement des intégrales...
A propos du titre de cet article, le jeu de l'interpolation Lagrangienne est un -grand- jeu à faire pendant les longs trajets en voiture. Un joueur pense à une personne, un objet, un animal ou autre et les autres joueurs doivent deviner ce dont il s'agit en posant des questions du type "portrait chinois". Exemple d'échange :
- Si tu étais un animal ?
- Un Lion !
- Si tu étais une couleur ?
- Rouge !
- Si tu étais un dieu grec ?
-Arès !
...il fallait évidement trouver Mars !...



/http%3A%2F%2Fstorage.canalblog.com%2F54%2F51%2F210892%2F121020798_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F97%2F40%2F210892%2F53900386_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F45%2F81%2F210892%2F51858304_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F32%2F90%2F210892%2F29169422_o.png)