Triangle de qualunquisme maximal

Prenez un stylo, un bout de papier, et dessinez-y un triangle quelconque... Peu importe la façon dont on s'y prend, le triangle que l'on va tracer aura toujours l'air d'être spécial : ou trop rectangle, ou trop isocèle, il y a toujours quelque chose qui ne va pas... Mais à quoi pourrait ressembler un triangle vraiment quelconque ?

Attention, spoiler : ce triangle EST quelconque !

Un triangle a une chance sur 4 d'être obtus...
Le plus banal des triangle est-il acutangle (avec tous ses angles aigus) ou obtusangle (avec un angle obtus) ? Et puis d'abord, peut-on vraiment qualifier de quelconque un triangle qui possède un angle obtus (il faut avouer qu'un triangle obtus a toujours l'air soit trop plat, soit trop bancal...)... On peut en fait montrer (en prenant les distributions de probabilités adéquates) qu'un triangle sur 4 seulement est aigu. C'est triste à dire, mais la majorité des triangles sont affreux :

Un triangle obtusangle trop bancal un autre trop plat...

Pour aboutir à ce résultat, on peut commencer par chercher la probabilité pour un triangle d'être aigu, en choisissant au hasard deux points dans un disque de rayon connu. On choisit donc un point A, un rayon R et on choisit au hasard (avec une loi uniforme) un point B (à distance r<R de A). On peut alors partager le cercle en plusieurs zones :

Si un point C du disque se trouve dans l'une des zones en rouge, le triangle ABC sera obtusangle. Il sera acutangle dans le cas contraire

Un triangle ABC sera alors obtusangle si son sommet C est dans l'un des domaines rouge d'obtusité, et acutangle sinon (On néglige les triangles droits au bord des zones rouges). Sans rentrer dans les détails, on peut trouver la probabilité du point C d'être dans une de ces zones rouges (en faisant un simple calcul d'aire). Des petites manipulations intégralo-probabilistes permettent de se ramener au cas où B a été choisit sur le rayon horizontal, et permettent de déduire que la probabilité du triangle ABC choisit au hasard dans le disque de centre A et de rayon R est :

En comparant avec l'aire πR² du cercle, on en déduit que le triangle a 25% de chances d'être acutangle, et 75% de chance d'être obtusangle (ce qui est chouette, au passage, c'est que ça ne dépende pas du choix de R)

Et le triangle le plus commun est...
On peut en fait s'intéresser ici à la forme des triangles plutôt qu'à leur taille : seuls les angles du triangle sont intéressants, puisque la connaissance des trois angles suffit à en connaître sa forme (ou plutôt, deux suffisent, puisque la somme des angles d'un triangle en vaut un plat). Quand on parle ici de triangle, on parle en fait de tous les triangles qui lui sont semblables.
Un bon moyen de représenter l'ensemble des triangles qui peuvent exister est d'utiliser une propriété des triangles équilatéral : "Dans un triangle équilatéral, la somme des distances d'un point intérieur aux côtés de ce triangle ne dépend pas du point considéré". Autrement dit, dans le triangle équilatéral LMN dessiné juste en dessous, la somme α+β+γ ne dépend pas du point F choisit. On va dire que α+β+γ=180.

Une paramétrisation de l'ensemble des formes de triangles

On fait alors correspondre à chaque point du triangle de représentation LMN le triangle d'angles α, β et γ. Les droites particulières du triangle de représentation se traduisent en triangles particuliers : Si le point F est sur le bord de LMN, on se retrouvera avec un triangle plat ; si celui-ci est sur l'un des côtés du triangle L'M'N', le triangle correspondant sera droit ; si celui-ci est sur l'une des médiatrice de LMN, le triangle correspondant sera isocèle. La zone verte correspond alors aux triangles acutangles, et la zone brune aux triangles obtusangles.

Quelques triangles : F₁, proche du bord, correspond à un triangle presque plat ; F₂, sur une médiatrice, correspond à un triangle isocèle ; F₃, sur un côté du triangle vert, est aigu ; F₄, proche du centre, est un triangle acutangle presque équilatéral

En considérant que prendre au hasard un triangle dans le plan signifie prendre au hasard (avec une loi uniforme) un point dans le triangle LMN, on retrouve bien que l'on a une chance sur 4 de piocher un triangle acutangle. (Ce qui prête à penser que cette approche est équivalente à l'approche précédente, conjecture tout à fait fondée)

Par un jeu de symétrie, on peut se contenter de regarder seulement ce qu'il se passe sur le triangle OL'N. C'est le moment de définir ce qu'est un triangle lambda. Plusieurs approche peuvent être choisie : l'approche aléatoire ou l'approche métrique

... le triangle des centres de gravité ! (approche aléatoire)
On peut dire que le triangle le plus ordinaire est le triangle moyen, au sens probabiliste. La probabilité que l'on choisit est celle des "fléchettes à l'aveugle" (loi uniforme), où l'on tire au hasard notre point dans le triangle OL'N. Le point moyen sera alors le centre de gravité du triangle en question, ce qui correspond à un triangle vraiment quelconque (dans un sens aléatoire).

On peut au passage trouver les triangles acutangles et obtusangles les plus quelconque (toujours dans ce sens aléatoire), en cherchant les centres de gravité des triangles OL'K et L'KN [où K est l'intersection entre (ON) et (L'M') ].

Triangles quelconques (au sens aléatoire) :
en bleu, le triangle scalène le plus quelconque
en vert, le triangle acutangle le plus quelconque
en brun, le triangle obtusangle le plus quelconque

... le triangle des centres du cercle conscrit ! (approche métrique)
Autre façon de voir les chose : le triangle le plus quelconque est le triangle le moins isocèle et le moins rectangle possible.  Dans notre triangle représentatif OL'N, ces propriétés à éviter correspondent au bord du triangle. En prenant la distance euclidienne classique, on peut dire que le triangle le plus quelconque correspond dans OL'N au point le plus éloigné du bord, qui se trouve être le point de concours des bissectrices (le centre du cercle inscrit).

De la même façon que dans l'approche aléatoire, on peut parler du triangle scalène le plus quelconque (le centre du cercle inscrit de OL'N) ou des triangles acutangles et obtusangles les plus quelconques (en prenant les centres du cercle inscrits à OL'K et L'KN).

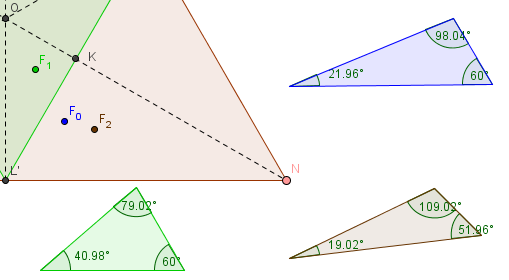
Triangles quelconques (au sens métrique) :
en bleu, le triangle scalène le plus quelconque
en vert, le triangle acutangle le plus quelconque
en brun, le triangle obtusangle le plus quelconque

Chacun appréciera selon son goût le triangle qu'il jugera le plus neutre de tous, mais ces différentes approches ne sont pas exemptes de problèmes. Il y a déjà le paradoxe du "plus petit entier qui n'est pas intéressant" : le fait que le triangle soit quelconque fait de lui un triangle plus vraiment quelconque. L'approche probabiliste du problème amène le paradoxe de Bertrand : il n'y a pas de procédé canonique pour tirer au sort un triangle (et donc, pour en trouver une moyenne). Les quelques auteurs qui se sont penché sur la question de la probabilité d'avoir un triangle obtusangle ont trouvé des résultats plus étranges, notamment P=97/50+π/40 (pour Langford) ou P<50% (pour Miles)...

---

Sources :
Le triangle le plus quelconque, par Jean-Marc Lévy-Leblond (Quadrature N°73, juillet-septembre 2009)

Comments

[Mr_Xen]

J'avais réfléchi au problème avec quelques figures, dans cet article :
http://pagesperso-orange.fr/gilles.josse/divers/maths/triangles-quelconques.pdf
Mais je n'avais pas trouvé de triangle le plus quelconque.
Sinon, bravo pour votre blog, que je fréquente régulièrement.

[El Jj]

JLT > Ce triangle acutangle (45°/60°/75°) est le fruit d'une troisième approche (l'approche "empirique"), que j'ai préféré zapper parce qu'elle ne se justifiait pas de la même façon que les deux autres. J'en profite pour dire au passage que le triangle obtusangle le plus quelconque au sens pifométrique est le triangle (30°/45°/105°).
J'ai réparé la coquille, une bête faute de signe. Ce qui est dommage, c'est que 97/50+pi/40 soit lui aussi supérieur à 1... L'erreur vient cette fois ci de ma source. La proba correcte trouvée par Langford est en tout cas d'environ 0.7252... .

[JLT]

Sinon, il doit y avoir une coquille dans l'expression P=97/50-π/40 (probabilité plus grande que 1).

[JLT]

J'aurais pensé que le triangle acutangle le plus quelconque est le triangle d'angles aigus a,b,c tel que la quantité

min(|a-b|,|b-c|,|c-a|,|90-a|,|90-b|,|90-c|)

est maximale. Les angles sont donc 45, 60, 75 degrés.

[Robyn Slinger]

Et sinon, je ne sais pas si le triangle "le plus quelconque" tombe dans le paradoxe du "plus petit entier inintéressant", ou plutôt dans l'univers orwellien : "tous les triangles sont quelconques, mais certains sont plus quelconques que d'autres".