De Usain Bolt à l'Eyjafjallajökull

6 juin 2010

Pour faire aimer les mathématiques aux non-initiés, on a tendance à parler des fractales :
"Regarde, si tu colories les points pour laquelle la suite des itérés de cette fonction polynôme est bornée, tu trouves ça... c'est joli, non ?!"
Ou alors, pour faire croire à la réelle utilité de l'arithmétique, on sort les nombres premiers (et toutes ses applications crypto-bancaires):
"Regarde, si tu place la suite des entiers en spirale et que tu colories les nombres premiers, tu trouve des droites, des fois... c'est marrant, non ?!"
Bien plus rarement, on parle des opérateurs différentiels :
"Regarde, si tu prends la transformée de Fourier de ton opérateur différentiel, tu peux connaître sa classification avec son symbole principal... Cool, non ?"

J'ai récemment promis, suite à une soirée un peu trop riche en fruits et légumes, un article sur les opérateurs différentiels à destination de ceux qui n'ont pas fait de maths depuis bien longtemps. Si vous cherchez une solutions aux équations de Navier-Stokes, passez votre chemin, je vais plutôt essayer de rester élémentaire...

Commençons par le commencement
Une des raisons d'être du calcul différentiel, c'est de s'amuser à chercher des relations entre la position en fonction du temps d'un objet et sa vitesse. Le problème "si je maintiens ma vitesse à 120 km/h, combien de mètre aurais-je roulé dans 21 minutes ?", c'est déjà un problème de calcul différentiel !

Soyons un peu plus pragmatique : une vitesse, qu'est ce que c'est exactement ?
On peut parler facilement de vitesse moyenne : si j'ai mis 9.69 secondes pour faire 100 mètres, c'est que j'ai fait du 10.3 m/s (37.2 km/h) en moyenne (obtenu en calculant le rapport entre la distance parcourue et le temps mis).
Pour parler de vitesse instantanée (celle donnée par un compteur de vitesse), il faut ruser un peu plus, en calculant la vitesse moyenne sur un intervalle plus petit. Reprenons l'exemple de ma course : à quelle vitesse ai-je passé les 50 mètres ? Un chronométreur m'a chronométré : j'ai mis notamment 4.64s pour faire 40m et 6.31s pour faire 60m. Ma vitesse moyenne sur l'intervalle 40m/60m est donc de (60-40)/(6.31-4.64) = 12 m/s (43,11 km/h). Cette valeur n'est toujours pas la vitesse instantanée du passage à 50 mètres, mais on s'y approche.

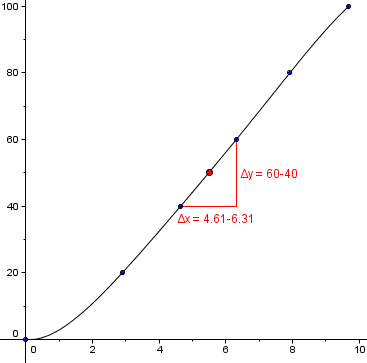
Usain
Distance parcourue en fonction du temps. Les points bleus correspondent à des mesures expérimentales. Pour connaître une approximation de la vitesse instantanée au point en rouge, on calcule le rapport Δy/Δx. Plus Δx sera petit, meilleure sera l'approximation.

Pour connaître la vitesse instantanée, il faudrait calculer la vitesse moyenne sur un intervalle encore plus petit, connaître par exemple le temps de passage aux 49e mètre et au 51e mètre...

En notant x(t) la position d'un point (ou la distance parcourue, ou n'importe quoi qui évolue avec du temps) en fonction du temps, sa vitesse instantanée en un moment t₀ est donc donnée par

lorsque $δ$ t tend vers 0. Cette vitesse v(t₀), on l'appelle habituellement dérivée de x. On la note volontiers x'(t₀) (quand on est matheux), ou bien ẋ(t₀) (quand on est physicien), ou alors dx/dt(t₀), ou même ∂x/∂t(t₀), ou...

Continuons par la suite
Avec l'invention/découverte de cette formalisation de la vitesse instantanée (que l'on attribue à Newton et Leibniz, à la fin du XVIIE siècle), et moyennant les découvertes en physique de Newton, tout un tas de problèmes comme "dans combien de temps la pomme touchera le sol", "comment dois-je régler l'inclinaison de ce canon pour lancer le boulet pile au bon endroit" ou "y'(t)=y(t)" ont été mis en équations et résolus dans la foulée (Ce que doit savoir faire un Terminale S à la veille du bac qui arrive...)

Une équation qui fait intervenir une fonction et ses dérivées (une équation "différentielle" [EDO] ou "aux dérivées partielles" [EDP]) ne peut pas forcément être résolue avec les armes algébriques classiques. C'est bien dommage, puisque la majorité (pour ne pas dire la totalité) des problèmes qui apparaissent en physique, en biologie, en astronomie, en chimie, en économie, en météorologie, en [...] font apparaître des équations différentielles, et seulement une infime partie d'entre elle peut être résolue de manière exacte... Heureusement, ce n'est pas parce qu'on ne sait pas les résoudre que l'on ne sait pas à en donner des approximations ! Tout le génie de nos analystes numériques, c'est de trouver les meilleurs moyens possible pour résoudre les problèmes qui émergent du monde réel. Et en général, ils y arrivent. Ça reste aujourd'hui un domaine de recherche très prolifique.

Terminons par la fin
(Avertissement : je ne sais pas bien ce que j'ai voulu prouver en écrivant ce paragraphe là...)
Prenons un exemple concret : un nuage de fumée noire ~~qui cherche à s'enfuir d'une île en se déguisant en chauve~~ provenant d'un volcan strombolien. On aimerait savoir comment le nuage va se déplacer, s'il va se dissiper, toussa.

volcan
Un volcan islandais
(Je mets cette illustration essentiellement pour mettre de jolis images dans mes articles)

Deux phénomènes sont là pour faire avancer le nuage : le phénomène d'advection (Le vente souffle sur le nuage) et le phénomène de diffusion (le nuage a tendance à s'homogénéiser). On peut rajouter à ça que du nuage est créé en permanence par le volcan. Il y a évidemment tout un tas d'autres paramètres qui rentrent en jeu, comme la densité des nuages qui traînent, par exemple, mais on va les négliger dans cette modélisation. On aboutit alors à l'équation :

Variation de la concentration de fumée en fonction du temps
=
variation induite par le vent
+
variation induite par la diffusion
+
apport du volcan

Le physicien qui passe par ici arrive à traduire ces phénomènes en équations, qui font apparaître des dérivées selon les variables x et t. Ça donne ceci (moyennant un bilan d'entrées/sorties pour l'advection, et la loi de Fick pour la diffusion):

c : concentration de fumée en fonction du point x et du temps t (inconnu, mais on suppose c(x,0) connu)
v : vitesse du vent en fonction du point x et du temps t (supposé connu)
k : coefficient de diffusion (dépend du type de fumée, du milieu ou des choses de ce genre, supposé connu)
f : apport du volcan (supposé connu)
On peut évidemment transformer les ∂c/∂c en gradient si on préfère faire le problème en 3 dimensions plutôt qu'en une...

L'inconnue, ici, c'est la fonction c (qui représente l'état du nuage en fonction du temps). L'équation, quant à elle, fait intervenir la fonction, ses dérivées (suivant ses différentes variables), et même la dérivée de sa dérivée. Tous le reste, ce sont des paramètres qui sont auront été soigneusement déterminées (expérimentalement, ou à partir d'autres ED). Autant le dire tout de suite : un truc comme ça se résout difficilement avec seulement du papier et un stylo...

C'est alors que les spécialistes des EDP interviennent, ceux que l'on appelle plus communément "météorologues". Ils ont toujours un bout de papier et un crayon de bois bien taillé, mais ils ont aussi des ordinateurs puissants. Leur boulot ne consiste pas simplement à mettre les donner dans l'ordinateur pour voir comment elles évoluent, mais à le programmer en faisant intervenir le maximum de données tout en maximisant la précision des calculs sans augmenter les temps de calculs...

mesalls
Évolution du nuage de centre après l'éruption de l'Eyjafjöll (images satellites)