Icosaèdre tronqué et couteau suisse de pétanque
Note : face à l'engouement montant (inversement proportionnel à celui pour Chewbacca) pour la tarte aux prunes de la FIPA 2010, la censure qui a fait ses preuves en 2006 sera de nouveau mise en place. Ainsi, la plupart des termes liés à la pétanque (vous savez, ce sport dans lequel des cerises courent après un couteau suisse pour le mettre au fond du calendrier) seront censurés, et remplacée par des termes moins équivoques. Et tant pis pour mon référencement Google et Wikio...
Icosaèdre tronqué... Un polyèdre semi-régulier (et même Archimédien) possédant 32 faces (12 pentagones réguliers et 20 hexagones réguliers), 60 sommets et 90 arêtes. Dit comme ça, on a du mal à voir à quoi je fais référence, mais quand on s'amuse à colorier en noir les faces pentagonales et en blanc les faces hexagonales, on tombe sur un modèle un peu moins sphérique du couteau suisse de pétanque utilisé depuis la tarte aux prunes au Mexique, en 1970 ! (Mais, juste pour me donner tort, les dernières compétitions n'utilisent plus l'icosaèdre régulier. Ainsi, la tarte aux prunes de 2006 au Timor oriental a utilisé un couteau suisse à seulement 14 découpages (le Teamgeist), et celle de cette année utilise un couteau suisse à seulement 8 découpages (le Jubilani), bien plus rond - et plus sensible à l'effet Magnus). En tout cas, cette tarte aux prunes est un moment bien choisi pour redécouvrir tous ces polyèdres !

A gauche, un icosaèdre tronqué
A droite, un couteau suisse de pétanque
Un polyquoi ?
De manière intuitive, un polyèdre est la version 3D des polygones : un objet à 3 dimensions composé seulement de faces planes (un cube est un polyèdre, une sphère n'en est pas). L'invention remonte à Euclide (IVe siècle avant J-C), et la définition de ce qu'est un polyèdre n'a cessé de changer, jusqu'à aujourd'hui, où le flou est tellement présent que personne ne sait vraiment ce qu'est un polyèdre...
Les polyèdres les plus intéressants sont évidemment ceux dont les faces sont des polygones réguliers (des polygones avec des côtés égaux). Bien que l'on puisse construire des polygones réguliers avec un nombre de côtés arbitraire, la 3ème dimension apporte son lot de complications : il n'existe que 5 polyèdres dont toutes les faces sont identiques, les solides de Platon :
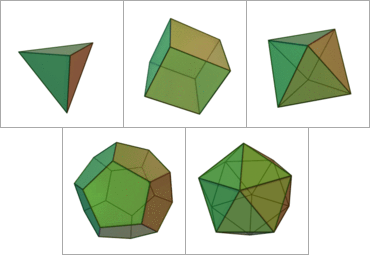
Les 5 solides platoniciens, bien connus des rôlistes :
- Le tétraèdre (3,3,3), composé de 4 triangles équilatéraux
- Le cube (4,4,4), composé de 6 carrés
- L'octaèdre (3,3,3,3), composé de 8 triangles équilatéraux
(obtenu en reliant les milieux des faces du cube)
- Le dodécaèdre (5,5,5), composé de 12 pentagones réguliers
- L'icosaèdre (3,3,3,3,3), composé de 20 triangles équilatéraux
(obtenu en reliant les milieux des faces d'un dodécaèdre)
Si le couteau suisse de pétanque n'est pas composé seulement de faces hexagonales, c'est tout bonnement parce que c'est impossible !...
Devant le trop peu de polyèdres réguliers, il a fallu étendre la définition. On dit donc qu'un polyèdre est semi-régulier si toutes ses faces sont des polygones réguliers, et si son groupe de symétries est transitif sur ses sommets (autrement dit, que les faces entourant les sommets soient toujours les mêmes). Cette seconde propriété permet de parler de configuration aux sommets : par exemple, la configuration (5,6,6) signifie qu'autour de chaque sommet, on trouve un 5-gone, un 6-gone et un 6-gone.
Dans les polyèdres semi-réguliers, on retrouve les 5 polyèdres platoniciens, deux familles infinies composées des prismes et des antiprismes, ainsi que les 13 (ou 15) solides platoniciens.

Quelques exemples de prismes (première ligne), et d'antiprismes (seconde ligne) semi-réguliers
Les prismes (4,4,n) sont composés de 2 polygones réguliers à n côtés, et de n carrés (le cube est un prisme)
Les antiprismes (3,3,3,n) sont composés de 2 polygones à n côtés, et de 2n triangles équilatéraux (l'octaèdre est un antiprisme)
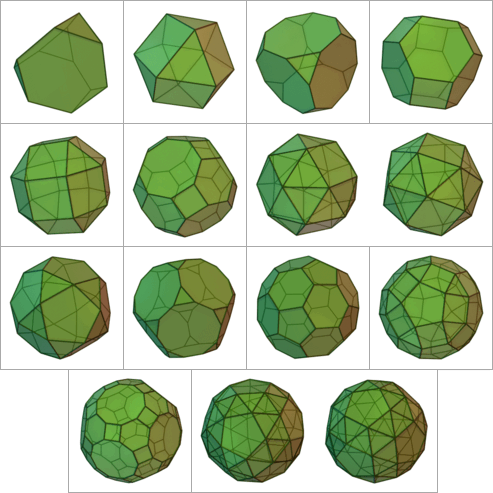
Les 13 (ou 15) solides archimédiens, rangés par groupes de symétries
- Le tétraèdre tronqué (3,6,6)
- Le cuboctaèdre (3,4,3,4)
- Le cube tronqué (3,8,8)
- L'octaèdre tronqué (4,6,6)
- Le petit rhombicuboctaèdre (3,4,4,4)
- Le grand rhombicuboctaèdre, ou cuboctaèdre tronqué (4,6,8)
- Les cubes adoucis (3,3,3,4), images miroir l'un de l'autre
- L'icosidodécaèdre (3,5,3,5)
- Le dodécaèdre tronqué (3,10,10)
- L'icosaèdre tronqué (5,6,6)
- Le petit rhombicosidodécaèdre (3,4,5,4)
- Le grand rhombicosidodécaèdre, ou icosidodécaèdre tronqué (4,6,10)
- Les dodécaèdres adoucis (3,3,3,3,5), images miroir l'un de l'autre
Revenons à nos moutons suisses
La star du jour, c'est quand même l'icosaèdre tronqué : un assemblage parfaitement régulier de pentagones et d'hexagones. D'après la classification de tous les polyèdres semi-réguliers, c'est le seul qui ne possède que des pentagones et des hexagones (l'icosaèdre non tronqué ne compte pas, il n'a même pas d'hexagones). Mais on peut quand même chercher ailleurs... Peut-on trouver d'autres polyèdres qui ressemblent plus ou moins à l'icosaèdre tronqué ? (ie, un polyèdre convexe (par forcément semi-régulier) composé d'hexagones et de pentagones réguliers, et qui ne se rencontrent que par 3 en chaque sommet)
Appelons p le nombre de pentagones, h le nombre d'hexagones, F le nombre de faces, A le nombre d'arêtes et S le nombre de sommets. Quelques relations unissent ces nombres :
- Le nombre de faces est égal au nombre d'hexagones plus le nombre de pentagones : p + h = F
- Le polyèdre étant convexe, la formule d'Euler (qui dit que pour n'importe quel polyèdre convexe, on a F-A+S=2) est vérifiée.
- Chaque pentagone apporte 5 sommets, chaque hexagone en apporte 6, et chaque sommet du polyèdre se retrouve 3 fois dans ces polygones. On a alors 5p + 6h = 3S
- De même, chaque pentagone apporte 5 arêtes, chaque hexagones apporte 6 arêtes, et chaque arête du polyèdre se retrouve dans deux de ces polygones : 5p + 6h = 2A.
Pour résumer les choses :
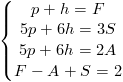
Quand on remplace dans la dernière équation F, A et S par les valeurs juste au-dessus, on se retrouve avec
![]()
Qui se simplifie en p=12... Il y aura forcément 12 pentagones réguliers dans notre polyèdre, mais on n'a pas plus d'informations sur les hexagones... On aura en tout cas F=12+h, A=30+3h et S=20+2h.
Les cas h=0 (S=20) et h=20 (S=60) fonctionnent bien, puisqu'ils permettent de retrouver l'icosaèdre et l'icosaèdre régulier. Mais ça marche aussi lorsque l'on prend 2, 3, 4, 11, 30, 260 ou 470 hexagones réguliers... (Seul le cas h=1 est contre indiqué, en fait). Mais ces questions sont plutôt du domaine de la chimie : sachant qu'un atome de carbone peut s'accrocher à trois de ses copains, quelles sont les structures régulières que l'on peut faire seulement en carbone ? La réponse est donnée par les fullerènes, découverts en 1985 (et qui ont permis à Harold Kroto, Robert Curl et Richard Smalley de gagner le Nobel de chimie). Ces molécules ont tout un tas de chouettes propriétés qui méritent plutôt d'être expliquées sur un blog de chimie/pharmacologie/cosmétique/électronique...

Exemple de fullerènes :
- C60, l'icosaèdre tronqué, appelé aussi buckminsterfullerène ou footballène (Des 1812 fullerènes ayant 60 sommets, c'est le seul qui n'a pas de pentagones se partageant une même arrête)
- C540 (12 pentagones, 260 hexagones)
- C70 (12 pentagones, 25 hexagones)
Les fullerènes interviennent aussi en architecture, lors des constructions de géodes (des polyèdres ressemblant le plus possibles à des sphères), composées de triangles équilatéraux, qui se réunissent par 6 en chaque sommet... En fait, non, il est impossible de faire des polyèdres avec des triangles équilatéraux qui se réunissent par 6 en chaque sommet ! Imaginons qu'il en existe un, et prenons son dual (le polyèdre que l'on trouve en reliant les centres des triangles). Si une géode parfaite existe, alors le polyèdre dual serait composé seulement d'hexagones réguliers, ce qui est impossible. On peut même dire mieux : dans les géodes, il y a toujours exactement 12 points où les triangles se réunissent par 5 !

Géode en cours de construction, par Stuart Radzinsky
On peut distinguer au moins deux sommets où se réunissent seulement 5 faces.
Ah, et tant que j'y pense...
Un petit truc inutile : les coordonnées des 60 sommets de l'icosaèdre tronqué centré en (0,0,0) (avec des arêtes de longueur 2) sont de la forme (0,±1,±3φ), (±1,±3φ,0), (±3φ,0,±1), (±2,±(1+2φ),±φ), (±(1+2φ),±φ,±2), (±φ,±2,±(1+2φ)), (±1,±(2+φ),±2φ), (±(2+φ),±2φ,±1)et (±2φ,±1,±(2+φ)), où φ = (1+√5)/2 est le nombre d'or, qui apparaît toujours là où il y a des pentagones.
Et un petit cadeau bonus : le patron d'un icosaèdre régulier, pour fabriquer son propre couteau-suisse de pétanque :
Le saviez-vous ? Le groupe d'isométries du ballon de football n'est pas le même que celui du ballon de volley !
Sources :
Wikipédia par ci, wikipédia par là, où wikipédia avec plein de jolis dessins de géodes... (La plupart des illustrations viennent de wikipédia)
Le site de JB Roux m'a bien servi également.




/http%3A%2F%2Fstorage.canalblog.com%2F77%2F73%2F210892%2F111515552_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F43%2F78%2F210892%2F106322231_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F16%2F78%2F210892%2F106207701_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F63%2F97%2F210892%2F99779882_o.png)