L'aiguille de Kakeya
Une aiguille. Voilà la seule chose qui a été nécessaire à Sôichi Kakeya pour lancer en 1917 le plus grand problème du XXe siècle ! J'admets, j'exagère un brin, mais le problème de l'aiguille de Kakeya fait parti de ces problèmes a priori difficiles qui ont été cassés par des idées toutes simples, mais redoutables !
La question posée par Kakeya est la suivante : comment retourner (de manière continue) une aiguille à 360° en balayant la plus petite aire possible. On appelle alors "ensemble de Kakeya" (ou 'ensemble de Besicovitch ") la surface balayée par l'aiguille.
Premières solutions
Première idée : faire bêtement tourner l'aiguille autour de son milieu. Ça balaye un disque, et donc une aire de π/4 (≃0.785...).

C'est un disque parfaitement rond
Mais on peut faire mieux. Cette fois-ci, on ne fait pas tourner l'aiguille autour de son milieu, mais autour de ses extrémités, en les alternant. L'ensemble balayé est un triangle de Reuleaux, avec une aire de (π-√3)/2 (≃0.705...)

Encore mieux : grâce à un ingénieux dispositif à base de cercles roulant à l'intérieur d'un plus grand cercle, on peut minimiser à nouveau l'aire balayée et former une deltoïde. L'aire balayée est maintenant de π/8 (≃0,393...), soit, celle du demi-cercle.

(C'est plus joli quand c'est animé...)
En 1925, on en est là : comment démontrer que la deltoïde est le plus petit ensemble de Kakeya ?
Plus malin !
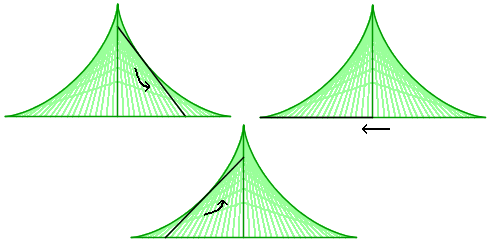
Eh bien, on peut pas ! En fait, on peut trouver des ensemble de Kakeya plus petit, et même très facilement : il ne faut pas oublier que déplacer une aiguille selon sa direction ne balaye aucune aire.
Ainsi, on commence avec l'aiguille verticale, et on la fait glisser comme une échelle le long d'un mur. Une fois tombée, on la translate horizontalement (ce qui ne balaye aucune aire), puis on la redresse.
Une ensemble de Kakeya étoilé à trois branches...
Bon, l'exemple n'est pas vraiment performant (l'aire balayée est d'environ 0.590...), mais on peut généraliser ce procédé . Au lieu de faire glisser l'aiguille sur un quart de plan, on peut le faire glisser sur un tiers de plan. En suivant le même principe de glissé-translaté, on forme une jolie étoile, qui est aussi un ensemble de Kakeya.

On commence par faire glisser l'aiguille sur un tiers de plan, puis on translate l'aiguille. En répétant deux fois l'opération, on balaye une étoile à 5 branches.
L'opération peut se généraliser à des étoiles à 7, 9, 11 branches... En augmentant le nombre de branches, l'aire de la surface balayée diminue, en tendant vers (5-2√2)π/24 (≃0.284...) (nombre calculé indépendamment par Bloom et Schoenberg en 1965).

Ensemble de Kakeya étoilé à 11 branches
Un ensemble comme celui-ci est appelé étoilé : tout segment reliant un point de l'ensemble à son centre est inclus dans l'ensemble. Cunningham démontrera en 1971 que si le domaine balayé est étoilé, alors il aura une aire supérieure à π/180 (0.029). Cela dit, personne n'a trouvé d'ensemble de Kakeya étoilé d'aire inférieure à 0.284.
Encore plus malin !
Outre ces résultats sur les domaines de Kakeya étoilés, le problème a explosé en intérêt quand, en 1928, Besicovitch est arrivé en clamant « il existe des ensemble de Kakeya aussi petits que l'on veut » !
Pour construire de tels ensembles, il faut comprendre comment on peut translater une aiguille d'un point A à un point B en balayant une aire minimale. On peut même faire cette opération en balayant une aire arbitrairement petite. L'explication tient en l'illustration suivante :

Pour faire passer l'aiguille de A à B, on commence par la translater loin, jusqu'en C. En ce point, on lui fait effectuer une petite rotation B que l'on souhaite atteindre. Il ne reste plus qu'une petite rotation à faire pour atteindre la position attendue.
Dans toute cette histoire, les seuls mouvements qui balayent un peu d'aire sont les rotations. Plus le point C est loin, plus l'aire balayée sera petite. Puisque l'on peut envoyer ce point aussi loin que l'on veut, on peut balayer une aire arbitrairement petite.
Il est maintenant l'heure de construire les ensembles de Kakeya ultimes : les arbres de Perron. Pour ça, on part d'un secteur circulaire, disons d'un sixième de cercle (ce qui permet la rotation d'un sixième de tour de l'aiguille). On le coupe en deux verticalement, puis on déplace l'un des deux demi-secteurs sur l'autre. Avec la technique de la translation sans balayage, c'est parfaitement légal !

Pour tourner l'aiguille d'un sixième de tour, on balayer moins d'un sixième de cercle.
Plutôt que de couper le secteur circulaire en 2, on peut le faire en 4, ce qui amène à une surface encore plus petite...

Il commence à y avoir beaucoup trop d'illustrations dans cet article...
Et on peut continuer comme ça, en diminuant à chaque fois l'aire balayée, pour obtenir les arbres de Perron. Il n'y a plus qu'à recopier six fois par symétrie pour obtenir un superbe ensemble de Kakeya, d'aire aussi proche de 0 que l'on veut !

Un ensemble de Kakeya d'aire approchant 0. Je ne crois pas que c'est un hasard s'il ressemble à l'œil de la Providence...
Super plus malin ?
Comme d'habitude, les mathématiciens se sont posé la question dans les dimensions supérieures, et, évidemment, ils ont trouvé. Il existe donc des ensembles de Kakeya infiniment fins en dimension 3, 4, ou plus...
La question qui suit naturellement est celle de la dimension fractale des objets que l'on a construits. En dimension 2, Davies a réussi à démontrer en 1971 que la dimension fractale d'un ensemble de Kakeya est toujours de 2. Autrement dit, un ensemble de Kakeya du plan est une surface d'aire nulle...
Il reste encore une question qui attend sa réponse : en dimension supérieure, à quel point la dimension fractale d'un ensemble de Kakeya est grande ? C'est pour une avancée sur la question (entre autres) que Terence Tao a obtenu en 2006 une médaille Fields ! La question des ensembles de Kakeya, pourtant anodine, a en fait des applications inattendues en analyse, notamment en analyse harmonique (les séries de Fourier et tout ce qui va avec).
(Et rappelez-moi de ne plus jamais faire d'articles avec autant d'illustrations, c'est vraiment trop long à faire...).
Sources :
En cheminant avec Kakeya, un power-point de Vincent Borrelli, avec encore plus d'illustrations.
Kakeya set, sur Wikipedia, avec encore plus d'informations.42



/http%3A%2F%2Fstorage.canalblog.com%2F84%2F61%2F210892%2F116475097_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F20%2F79%2F210892%2F104082950_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F49%2F06%2F210892%2F98803495_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F86%2F89%2F210892%2F85831746_o.png)