Just another Huffman tree
La nétiquette, c'est un ensemble de règles à suivre pour être un gentleman des internets, une charte implicite que tout le monde se devrait de suivre. Par exemple, dans son point 2.1.1 relatif aux bonnes règles d'usage du courrier électronique, la nétiquette requiert :
« Soyez conscient de la longueur des messages que vous envoyez. Annexer de grands fichiers, tels que des documents en Postscript ou des programmes, peut rendre vos messages si grands qu'ils peuvent ne pas être transmis ou au moins consommer une part exagérée de ressources. Une bonne règle sera de ne pas envoyer de fichier dépassant les 50 Ko. Comme alternative, réfléchissez au transfert de fichier, ou à découper le fichier en morceaux plus petits et à les envoyer séparément. » netiquette.fr
Il faut d'autant plus faire attention que 50 ko, c'est très vite atteint !... Bon, la nétiquette date de 1995, un temps où les modems 56k chantaient de la dubstep.
Mais il faut se souvenir qu'un gentleman n'envoie pas de fichier trop lourd à ses amis. Non, il commencera par le compresser à l'aide d'un logiciel adéquat, en s'assurant que son ami sache comment décompresser ce fichier.
Mais d'ailleurs, comment ça marche, la compression de fichiers ? De nombreuses méthodes existent aujourd'hui, mais la première d'entre toutes, c'est quand même la méthode de Huffman, qui n'a aujourd'hui rien perdu de sa superbe. En ce dimanche, parlons de Huffman et de ses arbres.
Saut ASCII
Je souhaite stocker, dans la mémoire de mon ordinateur, la phrase suivante « je ne suis qu'une phrase d'exemple mais j'ai quand même un cœur ». Et comme je suis exigent, je veux le faire de la façon la plus économique possible. Le gros problème, c'est que la seule chose qu'il est réellement possible de stocker dans la mémoire d'un ordinateur, ce sont des petits bouts d'information, des 0 et des 1 (les bits). Ma phrase d'exemple, elle, contient quand même 21 caractères différents, ce qui est sensiblement plus grand que 2.
Du coup, la première idée géniale est de regrouper les bits par groupe de 8 (les octets). Avec 8 bits, on peut fabriquer tout de même 256 nombres. Il suffit d'associer à chaque caractère un des 256 octets possibles, et le tour est joué.
On va dire que le « j » est codé par 01101010, que le « e » est codé par 01100101 ou que l'astérique est codé par 00101010 !
C'est ce que se sont dit dans les années 60 les créateurs de la convention de codage ASCII, histoire d'uniformiser tout ce qui prééxistait. Au final, le codage ASCII permet de coder 127 caractères, dont 95 caractères effectivement affichables, chacun codable sur 7 bits seulement, ce qui est bien suffisant pour les américains de l'époque. On se garde de côté le huitième bit de l'octet, il pourra nous servir à l'occasion.
La phrase « je ne suis qu'une phrase d'exemple mais j'ai quand même un cœur » se codera en ASCII (presque) par
01101010 01100101 00100000 01101110 01100101 00100000 01110011 01110101 01101001 01110011 00100000 01110001 01110101 00100111 01110101 01101110 01100101 00100000 01110000 01101000 01110010 01100001 01110011 01100101 00100000 01100100 00100111 01100101 01111000 01100101 01101101 01110000 01101100 01100101 00100000 01101101 01100001 01101001 01110011 00100000 01101010 00100111 01100001 01101001 00100000 01110001 01110101 01100001 01101110 01100100 00100000 01101101 00111111 01101101 01100101 00100000 01110101 01101110 00100000 01100011 00111111 01110101 01110010
L'ASCII est cependant incapable de coder des caractères farfelus comme « ê » ou « œ ». Tant pis, ils auront été codé par 00111111 (« ? »).
Au final, avec ce codage, on s'en sort avec un texte codé sur 63 octets, soit 504 bits (ou 441 bits si on enlève tous les '0' inutiles au début de chaque octet). C'est quand même beaucoup. En plus, on s'est fait flouer, puisqu'on a perdu deux caractères essentiels à l'intégrité de la phrase.
Ce qui serait parfait, c'est de compresser cette série de bits, mais sans perdre aucune information sur la phrase.
De l'inégalité patente entre les caractères
La norme ASCII est profondément égalitariste : que l'on soit un caractère cool comme le « j », une caractère fréquent comme le « e » et l'espace, ou un caractère inutile comme le «|», on est logé à la même enseigne, sur 8 bits. Une idée géniale, ça serait de coder sur peu de bits les caractères très utilisés, et sur plus de bits les caractères superflus.
C'est en fait le principe du code Morse : une lettre fréquente est codée par un signal rapide (le « e » est codé par « · »), alors qu'une lettre rare est codée par un signal plus long (« y » est codé par « — · — —») .
Faisons ça, toujours sur la même phrase d'exemple. L'espace et le « e » sont fréquent, on les code sur un seul bit ; le « x » et le « c » sont rares, on les code sur 4 bits :

Ainsi codée, la phrase sera :
01110011 01000001 10010000 01000011 01010000 11011101 01110101 00011000 10101011 00001100 11000110 10110010 10000110 11110000 00100001 00001000 11010000 110
On s'en sort maintenant avec seulement 139 bits ! Le progrès est énorme ! Oui, mais... Comment on va décoder ça ? Les 4 premiers bits sont 0111, qui peuvent se traduire par « je », mais aussi par « na » ou par « _eee ». Impossible de trancher, on a fait tout ça pour rien.
Pour ne pas avoir ce soucis d'ambiguïté, il nous faut un "code préfixe" ; autrement dit, un système de codage binaire où le code d'un caractère ne doit pas pouvoir être prolongé de façon à former le code d'un autre caractère. Ainsi, si l'on décide que l'espace est codé par 0, le codage d'aucun autre caractère ne doit pouvoir commencer par zéro.
C'est sur ce principe que se base la norme UTF-8 (la norme de codage de caractère la plus utilisée) : un caractère sera codé sur un ou plusieurs octets. Si le premier octet commence par 0, c'est qu'il est codé sur un seul octet selon la norme ASCII, dans le cas contraire, le caractère est codé sur plusieurs octets, et il faut se référer à la base de donnée idoine.
Compression de Huffman
Il me faut donc un code préfixe pour coder « je ne suis qu'une phrase d'exemple mais j'ai quand même un cœur » en utilisant le minimum de bits. La construction d'un tel codage, on la doit à David Albert Huffman, qui a mis au point l'algorithme qui suit lors de sa thèse de doctorat en 1952.
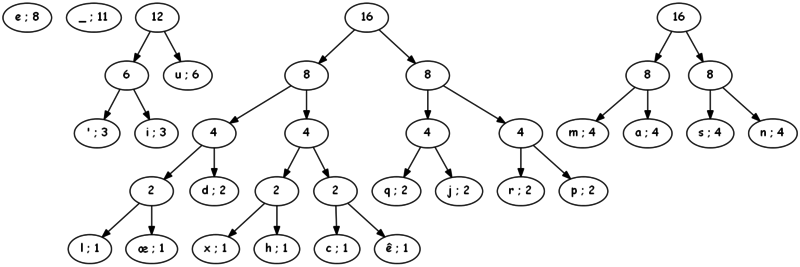
Pour cela, on commence par trier par ordre croissant de présence les caractères qui nous intéressent :
Puis, on prend les deux arbres de plus petit poids (ici, « l » et « œ », chacun de poids 1), puis on les réunis de façon à former un arbre binaire, qui sera alors de poids 1+1 = 2. L'arbre ainsi formé est alors remis à sa place, selon l'ordre croissant des poids.
On poursuit le processus, en réunissant à chaque étape les deux caractères (ou arbres précédemment formés) de plus petit poids sous une même bannière, dont le poids est la somme des deux poids :
(...)
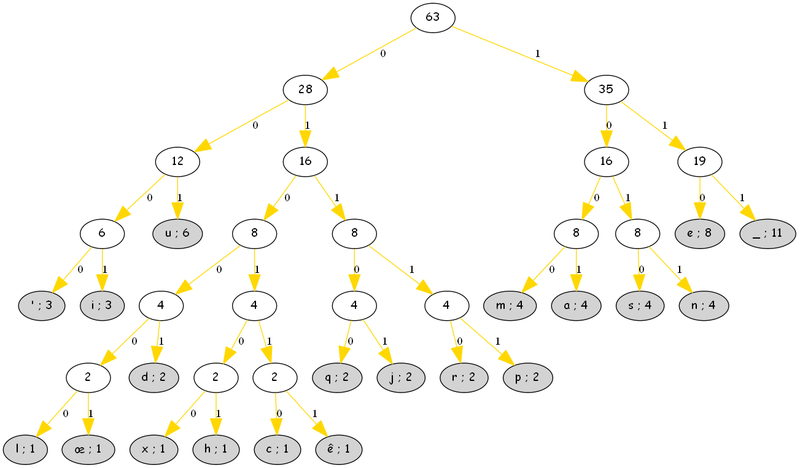
Finalement, après 19 étapes, on obtient un arbre complet, où les feuilles sont les caractères que l'on cherchait à coder. Le code, il est tout trouvé : en partant du haut de l'arbre, on codera '0' si l'on descend à gauche, et '1' sinon.
L'arbre codant / décodant
Ainsi, 001 codera « u » ou 01101 codera « j ». Par construction de l'arbre, les caractères les plus fréquents seront au plus prêt de la racine et demanderont une chaîne courte de bits, tandis que les caractères les plus rares seront codés par une chaîne plus longue.
Finalement, ma phrase initiale peut être codée sans aucune ambiguité (grâce à l'arbre) sur 249 bits (32 octets) par
01101110 11110111 10111101 00010001 10101110 11000010 00000110 11110111 01111010 10101110 10011010 11011101 00100001 10010100 11010000 11110100 00110111 10001001 00011010 11101101 00001001 00011110 11000011 00110110 10011111 00001011 11000110 11100110 11111010 11001000 10010111 0
Cela représente tout de même un gain de 50% par rapport au codage ASCII. Il est d'ailleurs impossible de le coder sur moins de bit avec un code préfixe. merci Huffman !
Si je dois déchiffrer cette séquence de bits, il suffit de la lire en suivant l'arbre. Les premiers caractères étant 01101, ils ne peuvent que coder le « j ».
Bon, il a quand même un hic : si je compresse ma phrase et que je la garde telle quelle, j'aurai du mal à retrouver la phrase initiale si je ne garde pas l'arbre de décodage quelque part. L'arbre doit être rattaché au fichier pour qu'il puisse être décompressé, et cet arbre a un poids : au moins 40 octets !
Finalement, mon message compressé pèsera environ 52 octets, ce qui ne représente plus vraiment un énorme gain par rapport au poids du message initial (63 octets). On peut éviter ce problème en utilisant un arbre générique, spécifique à la langue du texte que l'on code (voir commentaires de l'aticle). Il n'y a alors plus besoin de transmettre l'arbre, mais la compression sera forcément moins importante.
Cependant, le surplus représenté par le codage de l'arbre devient négligeable dès que les fichiers deviennent imposant (à partir de quelques ko).
L'algorithme de Huffman est utilisé par la plupart des logiciel de compression (WinZip, 7-Zip, WinRar...), mais il est le plus souvent couplé à un algorithme de compression de type LZ, qui commence par chercher et éliminer les redondances dans le fichier que l'on cherche à compresser.
Je terminerai par un fait tout à fait intéressant qui n'a rien à voir avec le sujet de l'article. David Albert Huffman ne s'est pas intéressé qu'à la compression de données, il a aussi découvert des méthodes d'origami tout à fait inédites en marge de ses travaux de topologie. Le résultat est particulièrement élégant :

Pavage origami, mis au point par Huffman.
Il est cependant déconseillé de le compresser.
Sources :
D.A. Huffman, A Method for the Construction of Minimum-Redundancy Codes, l'article original de Huffman
E. Davis & friends, Reconstructing David Huffman's Origami Tessellations, d'où provient l'illustration de l'origami