2020+1 (Cette nouvelle année est-elle intéressante ? Episode 12)
Incroyable ! J'ai toujours un blog ! Et comme nous sommes à l'aube d'une nouvelle année, il est l'heure de se livrer à la tradition annuelle : consulter les astres de l'OEIS, et révéler ce que les arcanes de la numérologie pourront prédire de l'année qui arrive.
Les prédictions de l'année passée se sont révélées parfaitement exactes, puisque l'année 2020 a comme prévu été "pas mal" (si l'on met bien entendu de côté cette anecdotique histoire de pandémie mondiale). Mais que nous réserve l'année 2021 ? Eh bien, elle sera...
Meilleure que 2020 !

Nombre de propriétés répertoriées par l'OEIS pour chaque année.
Conjecture : le nombre de propriétés reflète l'intérêt d'une année.
Avec ses 299 propriétés répertoriées par l'Encyclopédie en ligne des suites entières, le nombre 2021 se révèle être assez riche. Il faut dire que le nombre 2021 a une décomposition en nombres premiers intéressante : 2021 = 43 × 47. Il s'agit donc d'un nombre semipremier, car il est le produit de deux nombres premiers. Mais ces deux nombres premiers ont la riche idée d'être consécutifs, ce qui n'est pas banal. La présence de petits chiffres permet aussi à ce nombre d'avoir des propriétés dans d'autres bases de numération (en particulier, les nombres qui s'écrivent 2021 en base 3 et 4 sont des nombres premier, puisqu'il s'agit de respectivement 61 et 137).
Le polyomino 12-zigzag possède 2021 ceintures [A060641]
Un polyomino est un assemblage de carrés unitaires joints par leurs arêtes, à l'image des pièces de Tetris. On dit qu'un polyomino est "ceinturé" lorsqu'il est complètement entouré par des copies de lui-même qui ne se chevauchent pas, et qui ne laissent aucune arête libre. Les rotations sont acceptées, mais pas les images miroirs.

Essayons de ceinturer un L-tétromino, le polyomino constitué de 4 carrés formant la lettre L.
Le polyomino A est parfaitement ceinturé par 5 copies de lui-même. La configuration qui entoure le polyomino B n'est pas valide, car l'une des copies est une image miroir. Le polyomino C est lui aussi mal ceinturé : deux copies se superposent, et une arête est laissée libre.
On peut alors se demander le nombre de façons de ceinturer un polyomino donné. Il y a par exemple 13355 façons de ceinturer notre L-tétromino. Il n'y a cependant que 3 façons de ceinturer l'ennéamino ci-dessous, qui est le plus petit des polyomino possédant cette propriété. Saurez-vous retrouver ces trois ceintures ?

Quant au polyomino appelé "12-zigzag", il possède exactement 2021 ceintures.

Un exemple de ceinture parmi les 2021 qui existent.
2021 est un nombre de la forme n² + n + 41 [A202018]
Pour n = 44, on a bien n² + n + 41 = 44²+44+41 = 2021. Cette propriété peut sembler particulièrement arbitraire, mais le polynôme n²+n+41 est en fait très intéressant. Pour toutes les valeurs entières de n comprises entre 0 et 39, le polynôme P(n) = n²+n+41 génère un nombre premier :
41, 43, 47, 53, 61, 71, 83, 97, 113, 131, 151, 173, 197, 223, 251, 281, 313, 347, 383, 421, 461, 503, 547, 593, 641, 691, 743, 797, 853, 911, 971, 1033, 1097, 1163, 1231, 1301, 1373, 1447, 1523, 1601
Au-delà de n=39, certains P(n) seront des nombres premiers (P(42)=1847, P(43)=1933, ...), et d'autres non (P(44)=2021, ...).
Cette propriété s'observe assez bien sur ce que l'on appelle la spirale d'Ulam, attribuée au mathématicien Stanisław Ulam. On raconte qu'il a découvert cette représentation des nombres premiers un peu par hasard, alors qu'il écoutait un exposé très long et très ennuyeux. Sur sa feuille, il a disposé les nombres entiers sous forme d'une spirale, puis il a colorié les nombres premiers.

Au premier abord, il n'y a rien à voir, mais si on pousse le dessin plus loin, on trouve cette spirale d'Ulam.

La spirale d'Ulam.
En bleu les nombres premiers, en rouge les nombres premiers de la forme n²+n+41 et en jaune les autres nombres (composés).
Ce que l'on observe d'étonnant dans cette représentation des nombres entiers, c'est la présence de lignes obliques, ce qui traduit un certain ordre dans les nombres premiers. La présence de ces diagonales traduit l'existence de polynômes de degré 2 (a.n²+b.n+c) qui donnent un grand nombre de nombres premiers.Les nombres premiers de la forme n²+n+41 forment des lignes remarquables.
En débutant la spirale en 41 plutôt qu'en 1, les nombres premiers de la forme n²+n+41 ressortent de manière encore bien plus évidente.

Est-il alors possible de trouver un meilleur polynôme P(n), qui donnerait uniquement des nombres premiers quels que soient la valeur de n ? On a par exemple le polynôme
P(n) = 36n²-810n+2753
qui donne des nombres premiers (éventuellement négatifs) pour n compris entre 0 et 44. Mais quoiqu'il arrive, il est impossible de trouver un polynôme à une variable qui ne donnerait que des nombres premiers. Il y a bien un polynôme de degré 26 qui fait exception. Il a 25 variables, et toutes ses valeurs positives sont des nombres premiers. Il ressemble à ceci :
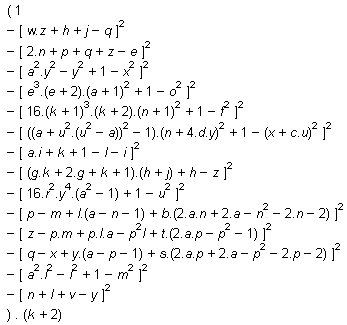
Il y a bien sûr une arnaque, quand on regarde la formule de plus près. le polynôme est de la forme (1-TRUC) × (k+2), où TRUC est une somme d'expressions au carré, donc, positif. Pour que le tout soit positif, il faut donc que TRUC soit égal à zéro, ce qui revient à résoudre 14 équations en même temps. Ce polynôme n'a en fait jamais généré autre chose que des nombres premiers très petits. Tout ça n'a aucun rapport avec 2021, mais je trouve ça tout de même intéressant.
2021 est le nombre de ϕ-partitions de 49 [A283528]
Pour expliquer ce qu'est une ϕ-partition, il faut expliquer ce qu'est une partition, et expliquer à quoi correspond ϕ.
Commençons par les partitions. Combien y a-t-il de façons d'écrire le nombre 7 sous la forme d'une somme décroissante d'entiers non nuls ? Détaillons :
7 = 1+1+1+1+1+1+1
= 2+1+1+1+1+1
= 2+2+1+1+1
= 2+2+2+1
= 3+1+1+1+1
= 3+2+1+1
= 3+2+2
= 3+3+1
= 4+1+1+1
= 4+2+1
= 4+3
= 5+1+1
= 5+2
= 6+1
= 7
Il y a donc 15 façons d'écrire 7 sous la forme d'une somme. On dit donc que 7 a 15 partitions. Le nombre 49, quant à lui, possède pas moins de 173525 partitions.
L'indicatrice d'Euler ϕ, maintenant. Combien de nombres entiers inférieurs au nombre 7 sont premiers avec 7 ? Il y en a 6 : 1, 2, 3, 4, 5 et 6 (puisque 7 est un nombre premier, tout entier inférieur est premier avec lui). On dit alors que ϕ(7) = 6. On a de même ϕ(1)=1, ϕ(2)=1, ϕ(3)=2, ϕ(4)=2, ϕ(5)=4 et ϕ(6)=2.
Une ϕ-partition d'un nombre n, c'est alors une partition de n qui reste vraie quand on remplace chaque nombre par son indicatrice d'Euler. Par exemple, la partition 7= 5+1+1 est une ϕ-partition, car ϕ(7) = ϕ(5)+ϕ(1)+ϕ(1). Le nombre 7 possède alors deux autres ϕ-partitions : 7=2+1+1+1+1+1 et 7=3+1+1+1+1. On ne compte par la partition 7=7, qui manque d'intérêt. Ce qui ne manque cependant pas d'intérêt, c'est le nombre 49 qui possède très exactement 2021 ϕ-partitions.
Mais aussi...
- 2021 est la concaténation de deux nombres entiers consécutifs, comme 1920 ou 2122 [A001704]
- Le carré de 2021 est 4084441. Le miroir de 4084441 est lui aussi un carré : 1444804 = 1202². Le nombre 2022 aura aussi cette propriété.[A035123]
- Il existe 2021 façons d'écrire 1/7 comme la somme de l'inverse de 4 entiers.
Par exemple 1/7 = 1/21+1/21+1/42+1/42 [A020327] - La 2021e décimale de π est un 8, la 2021e décimale de e est un 8, la 2021e décimale du nombre d'or φ est un 8. Chouette coïncidence. [A266002]
Et la santé !
Solution du puzzle : les trois ceintures de l'ennéamino :




/http%3A%2F%2Fstorage.canalblog.com%2F97%2F87%2F210892%2F113994993_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F42%2F13%2F210892%2F108236323_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F72%2F15%2F210892%2F107004083_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F98%2F97%2F210892%2F92096273_o.png)