Une chance sur beaucoup
Y a-t-il plus de chance de gagner au loto ou de battre Federer au tennis ? Y a-t-il plus de chances de tomber deux fois de suite sur une même blague carambar ou de mourir un vendredi 13 ? Je ne vois qu'une façon de répondre à ces questions : consulter ce schéma.
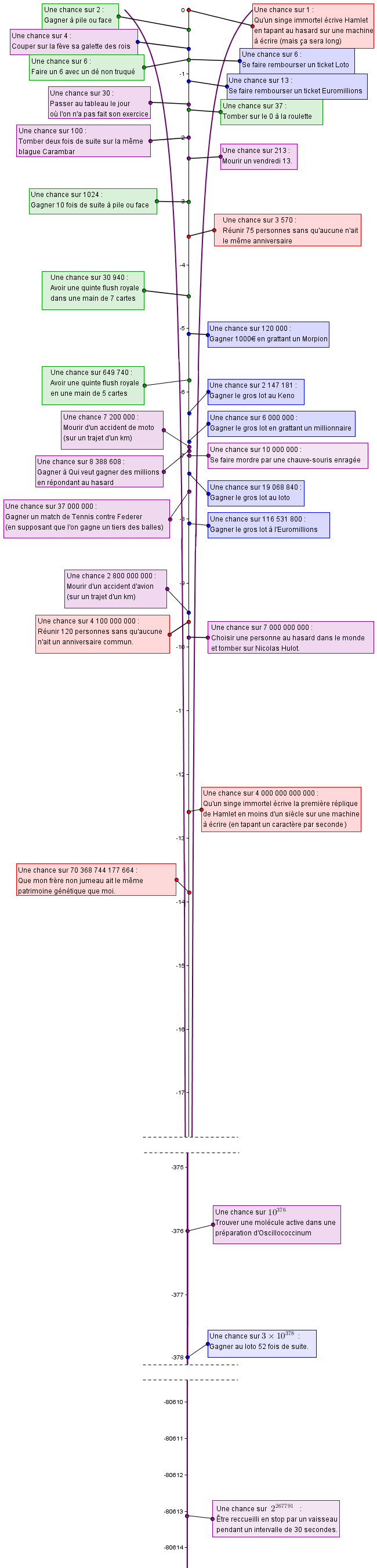
Remarques :
Une chance sur 4 : pour une galette 8 personnes de 30cm de diamètre.
Une chance sur 30 : c'est une proba conditionnelle !
Une chance sur 7 200 000 : Statistiques avion / moto (2001-2002)
Une chance sur 4 000 000 000 000 : avec une machine à écrire à 50 touches, la première réplique "Who's there?!" comportant 13 caractères.
Vous aimerez peut-être :
Commentaires sur Une chance sur beaucoup
- Y en a beaucoup qui m'ont fait rire par leurs références ! Quelques-unes mériteraient des explications… Mourir un vendredi 13 ? Gagner un match de tennis contre Federer ?
Et ce fameux une chance sur 30, veut-il dire qu'on passera au tableau la seule fois sur 30 où on n'a pas fait son exercice ?
Ou qu'on ne fait jamais ces exercices et qu'on a comme tous les jours une chance sur 30 de passer au tableau ?
- Terry Laire > Sur une année, il y a en moyenne un peu plus d'un vendredi 13. Quand on fait les calculs sur 28 ans, ça donne 1/213. Pour le match contre federer, je te renvois à cet article : http://eljjdx.canalblog.com/archives/2009/06/06/13908258.html .
Le 1/30, c'est la proba d'être appelé au tableau (pour une classe de 30 élèves, of course). Mais si on ne fait jamais son exercice, la proba d'être appellé au moins une fois un jour où le travail n'est pas fait augmente largement ! - Excellent !
Mais il y a au moins 2 exagérations :
- 1 chance sur 1 : je ne doute pas qu'un singe immortel arrive à écrire Hamlet au hasard, mais il n'y a aucune raison que ce soit FORCEMENT long. Si on a de le chance (non quantifiée !), cela peut aller assez vite (si on n'a pas de chance, il peut aussi écrire du Marguerite Duras).
- 1 chance sur 10^376 : c'est la probabilité de trouver une molécule de foie (ou de coeur) de canard de barbarie dans l'Oscillococcinum. Mais qu'elle soit active contre quoi que soit (la grippe ?), c'est autre chose... - C'que j'aime dans ce blog, c'est que dès que ya une nouveauté, jsais que j'aurai un truc à raconter le lendemain au déjeuner, assis à une table d'autres étudiants de maths.
Et bah là, j'ai de quoi intéresser plein de profanes avec des chiffres très rigolos pendant au moins une dizaine de repas !
Merci beaucoup ! - 10^376 oscillococcinumComment arrive-t-on à 1 chance sur 10^376? Car 10^376 est très supérieur au nombre de molécules de l'univers donc toute préparation initiale qui comporte 1 molécule d'oscillococcinum comporte moins de 10^376 autres molécules. Si elle en comporte n et qu'on en tire une au hasard on a 1 chance sur n de tomber dessus. Donc un résultat plus grand que 1/10^376. (Il y a bien un flacon en vente quelque part qui va contenir une molécule active même si, à force de dilution, la plupart n'en comporteront effectivement aucune)
- votre timelineBonjour,
Je cherche depuis longtemps un outil pour dessiner des timelines ou fresques historiques.
Je trouve la votre particulièrement jolie. Pourriez-vous expliquer comment vous avez fait ? Si vous avez vous-même créé l'outil, pouvez-vous le mettre à disposition (par exemple avec une licence libre du type Creative Commons) ?
Je suis enseignante en mathématiques et cela m'aiderait beaucoup à préparer mes cours. Merci d'avance.
Nathalie Carrié - Tom > Je voulais laisser encore un peu de magie !
Alainf50 > Pour la calculer, je suis parti du fait qu'il n'y a exactement une molécule originale après 12 dilutions à 1%. A la 13e dilution, on a une chance sur 100 de trouver cette dilution. A la 200e dilution, on trouve la proba que je donne.
nathalierun > J'ai fait cette fresque avec Geogebra, mais ce fut très laborieux, c'est loin d'être l'outil idéal ! - GalettePour la galette, j'avais fait le calcul et je tombais à peu près sur le même résultat... pour les détails : http://omnilogie.fr/O/De_la_probabilit%C3%A9_de_tomber_sur_la_f%C3%A8ve_en_coupant_la_galette_des_rois
- OscillococcinumOui je comprends bien ton calcul. Mais cela ne signifie-t-il pas qu'en prenant un flacon au hasard d'oscillococcinum on est (quasiment)sûr de ne pas trouver une molécule active? C'est à dire qu'il n'y a aucun flacon au monde contenant une seule molécule active? Car sinon je fais l'expérience en pensée de mettre tous les flacons dans un seul grand flacon et je tire au hasard et comme le nombre de molécules est de très loin inférieur à 10^376 j'aurai une proba bien supérieure à 1/10^376 d'en tirer une active. C'est ce petit paradoxe qui me titille dans ce
résultat. - OscillococcinumAlainf50 > Il n'y a pas de paradoxe, c'est que tu supposes la méthode de production de l'Oscillococcinum (la dilution K) similaire à celle de la plupart des produits homéopathique (la dilution CH)
En ceci que, dans la dilution CH la solution est conservé et diluée entièrement à nouveau pour faire, à chaque étape, 10 fois plus de produit (jusqu'à 30 fois de suite, ce qui parait très compliqué, puisqu'on atteindrais alors des quantités de produit 10^30 fois supérieur à la quantité initiale... Alors 200 fois, le paradoxe viendrais simplement du fait que c'est matériellement impossible)
Mais dans la dilution K seul 1% (à la louche) de la solution est conservé (et 99% simplement jetée aux orties) et diluer à nouveau, 200 fois d'affiler jusqu'à obtenir le produit qui imprégneras les granules de lactose qui servent de support au produit d'un seule tube d'Oscillococcinum.
A chaque dilution la quantité de produit n'est donc pas multiplié par 10.
Et en prenant tous l'Oscillococcinum du monde tu ne retrouvera pas nécessairement cette molécule.
En gros, si on part avec une seule molécule avant la 13ème dilution (postulat), on à simplement 9 chances sur 10 qu'elle parte aux orties à chaque nouvelle dilution... 188 fois d’affiler !
Cette proba est exactement la même que de tirer 188 "1" d'affiler sur un dé à 10 faces, ou qu'une section de 188 décimales d'affilé de PI dont la première est choisie aléatoirement soit "4242424242424242424242..."
(par contre je n'ai pas saisie pourquoi JJ multiplie ce nombre de 188 par deux pour obtenir 10^376, mais je sent qu'en disant ça je vais passé pour un crétin... )
En revanche si on part du principe que le concept de homéopathie est que le soluté transmet son "activité" au solvant par réorganisation de sa structure moléculaire, on peut en conclure que TOUTES les molécules sont, au final, actives.
La probabilité de trouver une molécule active dans une tube d'Oscillococcinum serait donc de 1/1...
D'un autre côté, comme tous le monde (y compris les plus illustres homéopathes) s’accordent à dire que finalement, l'oscillocoque n'existe pas, on peut dire qu'il n'y à AUCUNE molécule active dans l'Oscillococcinum...
Sauf si on prend "active" au sens large et qu'on tiens compte de la composition des granules, du lactose, qui est au moins dextrogyre (et donc actif sur la limière) et hémi-acétylique (chimiquement actif entant que réducteur)... Mais là on sort un peut des maths pour jouer sur les mots je crois
- A propos de 42Je n'avais pas très bien compris l'histoire du 42... Je suis donc allé vérifier si j'ai bien pigé et j'ai cliqué sur le dernier article à ce jour (Conjecture ABC), effectivement le 42 y est...
Seconde tentative l'article titré "ENIGMA" (http://eljjdx.canalblog.com/archives/2012/05/27/24326750.html) n'en contenait point !
Je m'en vais vérifier les autres...
Ai-je mal compris ?
Plus de chances de remporter le gros lot en répondant tout au hasard chez JP Foucault qu'en jouant au loto, excellent !
Nouveau commentaire
