Le plus doré de tous les nombres
Depuis quelques jours, la pub pour la nouvelle collection des éditions machin tourne en boucle dans les coupures pubs de TF1. Après Les Voyages de Charlie, Heidi en VHS et Les Secrets de style de Mary-Kate & Ashley, c'est le numéro 1 de la collection Le monde est mathématique qui vient d'arriver chez tous les marchands de journaux, pour un prix défiant toute concurrence. L'idée de la collection est de découvrir que tout ce qui nous entoure ne peut se comprendre sans les mathématiques. Excellente idée !
Au sommaire du numéro un : le nombre d'or, le langage mathématique de la beauté.
FFFFFFFUUUUUUUUUU !
Soyons clairs : utiliser le nombre d'or comme fil rouge du premier numéro d'une collection consacrée aux mathématiques, c'est aussi malin que de demander à Élizabeth Teissier de préfacer un ouvrage d'astronomie. Certes, le nombre d'or est un nombre qui apparaît naturellement quand on fait un peu de maths. Certes, on le retrouve plus ou moins dans quelques œuvres d'art... Mais rien ne justifie le nombre d'ouvrages qui ont été écrits sur le nombre d'or, où chaque chapitre peut se résumer par "regardez, il y a le nombre d'or là".
Mathématiques du nombre d'or
Le nombre d'or, donc, c'est le nombre 1,618033989...., noté Փ (phi, comme Phidias, concepteur du Parthénon). Mathématiquement, on peut le définir comme l'unique solution positive de l'équation x²=x+1, qui est donc égale à :
![]()
Du coup, cette relation confère à Փ des propriétés hallucinantes comme :
Փ²=Փ+1
1/Փ=Փ-1
Ce qui est aussi intéressant que de dire que l'inverse de √2 est sa moitié.
Son autre propriété mathématique naturelle est sa relation avec la suite de Fibonacci (1, 1, 2, 3, 5, 8, 13, chaque terme de la suite s'obtient en additionnant les deux termes précédents), puisque le rapport de deux nombres consécutifs tend vers Փ à l'infini. L'expression fonctionnelle de la suite de Fibonacci fait également apparaître Փ.
Il apparaît plus ou moins en géométrie dans le pentagone régulier et dans ce qui lui est lié, notamment dans les coordonnées canoniques d'un dodécaèdre régulier et d'un icosaèdre régulier (2 des 5 polyèdres de Platon, ce qu'il y a de plus régulier chez les polyèdres).
Il réapparaît enfin en arithmétique modulaire. Il se trouve que le corps ℚ(√5) où vit naturellement Փ est particulièrement intéressant, puisque l'anneau de ses entiers est euclidien. C'est pas grand-chose, mais c'est notable.
L'intérêt purement mathématique du nombre d'or s'arrête là...
Esthétisme du nombre d'or
Remontons un peu le fil des évènements. La première apparition en public du nombre d'or a lieu sous la plume d'Euclide. A cette époque-là, la notion de nombre n'est pas vraiment comprise, mais cela ne l'empêche pas d'étudier dans son livre XIII ce qu'il se passe quand "une ligne est coupée en extrême et moyenne raison", autrement dit, quand on pose un point C sur un segment [AB] tel que AB/AC=AC/BC. Il démontre par exemple que (1+Փ/2)²=5(Փ/2)². Le rectangle d'or apparaît également, mais aucune trace d'un intérêt esthétique.
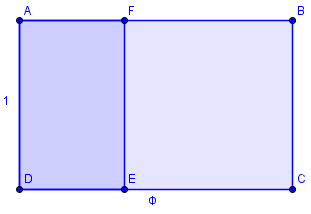
ABCD est un rectangle d'or : en lui retirant un carré (FBCE), on obtient le rectangle AFED, sembable au premier (donc, d'or). Notons que F coupe [AB] en extrême et moyenne raison.
Le nombre d'or réapparaît en filigrane au Moyen-âge, dans les écrits de Al-Khawarizmi (puisqu'il y parle d'équation de degré 2) et chez Leonardo Pisano (aka. Fibonacci), qui parle de lapins et donne naissance à sa suite. Aucun d'entre eux ne voit de quelconque liens avec le partage d'une ligne en extrême et moyenne raison...
A la renaissance, c'est chez le moine franciscain Luca Pacioli que la dimension mystique du nombre apparaît vraiment, dans le livre De divina proportionne. Pour lui, le partage en extrême et moyenne raison ne peut être que l’œuvre de Dieu, et ne peut être appelé autrement que "divin". Pour son bouquin, Pacioli a fait appel à un illustrateur plutôt reconnu : Leonard de Vinci. En parlant de De Vinci, il faut quand même savoir qu'il n'a jamais parlé du nombre d'or. En particulier, la proportion parfaite de l'homme de Vitruve n'est pas fondé sur la proportion divine, mais sur un découpage en quarts et huitièmes. Les canons harmoniques de l'époque parlent plus de rapports d'entiers (comme 5/8 ou 2/3) que de nombre d'or.
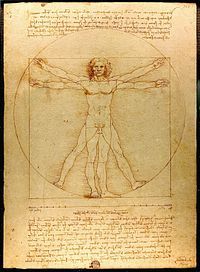
"Mais si, regarde, le nombre d'or apparaît dans l'homme de Vitruve ! Il faut que tu divises le côté du carré par le rayon du cercle !" (le rapport réel entre les deux est plus proche de 1.7 que de 1.6)
Au fil du temps, l'intérêt porté au nombre d'or décroit, jusqu'au XIXe siècle où Adolf Zeising, professeur de philo à Leipzig et Munich, le redécouvre. Il fonde une théorie de l'esthétisme centrée sur le nombre d'or, et part du principe qu'elle est rétroactive. Sa théorie (plus ou moins fumeuse) s'applique donc à la morphologie, à l'architecture, à la peinture... Son crédo ressemble à "Si tu ne trouves pas le nombre d'or dans [telle oeuvre], c'est que tu as mal cherché". C'est ainsi que l'on retrouve après ajustement le nombre d'or dans les plans du Parthénon et dans l'oeuvre de Mozart ou que le nombre Փ√Փ peut être trouvé sous le sabot d'un cheval.

"Là, plus personne ne pourra douter que le Parthénon a été dessiné suivant le nombre d'or"
Le point Godwin de l'histoire du nombre d'or est atteint dans les années 40, dans le livre Le nombre d'or, clé du monde vivant de Dom Neroman. Pour lui, le nombril doit diviser la hauteur d'un être humain selon le nombre d'or. Si une race n'atteint pas cette perfection, c'est qu'elle n'est pas assez évoluée. Comme par hasard, ça tombe sur "la Juive" et sur "la jeune négrille de l’Afrique équatoriale"...
Bref. En fait, en cherchant bien, n'importe quel nombre peut se retrouver n'importe où. J'ai d'ailleurs trouvé une relation très intéressante entre le nombre d'or et la réponse à la grande question sur la vie, l'univers et le reste :
![]()
Reste cette question en suspens : un rectangle d'or, c'est beau, ou pas ? Une expérience a été menée en 1876 par Gustav Fechner, et le résultat est sans appel : les rectangles aux proportions s'approchant de celles du rectangle d'or sont jugés plus beaux. Et puis, l'expérience a été réitérée en tenant compte des biais expérimentaux, et on a pu découvrir qu'il n'y a pas de rectangle plus beau qu'un autre.
Les rectangles de la vie quotidienne confirment finalement l'idée que le nombre d'or n'a rien de particulier. Les formats normalisés de papier A3, A4, An sont de ratio √2:1 (ce qui permet de garder les même proportions une fois coupé en 2) ; les formats américains ne portent pas de trace du nombre d'or, pas plus que les formats de télé, de cinéma ou de tableaux d'art. Seules les cartes bleues ont un format s'approchant de celui du rectangle d'or...
Après, si un artiste décide d'adopter le nombre d'or pour faire ses dessins, libre à lui. Mais du coup, ce n'est plus un hasard si on le retrouve en divisant n'importe quoi par n'importe quoi...

Comme par hasard, on retrouve le nombre d'or dans Le sacrement de la dernière cène de Dalí
... En fait, cela n'a rien d'un hasard, c'est complètement volontaire. D'ailleurs, il y a représenté un dodécaèdre régulier...
Sources :
La numérologie du nombre d'or, Pour la Science, Septembre 2000
Wikipédia, aussi (et pour cette photo du Parthénon)



/http%3A%2F%2Fstorage.canalblog.com%2F82%2F99%2F210892%2F116837441_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F11%2F12%2F210892%2F104995347_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F11%2F88%2F210892%2F85145948_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F42%2F88%2F210892%2F71308477_o.jpg)