La dualité. Mesdames et messieurs.
Il n'y a pas que les physiciens quantiques et les philosophes qui ont le monopole de la dualité. Les mathématiciens ont aussi leur mot à dire, et ils ne se sont pas privés : dual d'un polyèdre, dual d'un graphe, dual d'un espace vectoriel, dualité de Poincaré...
Ma dualité préférée est celle de la géométrie projective, le domaine de la géométrie qui étudie les notions de perspectives. Cette dualité permet sans effort de fabriquer plein de nouveaux théorèmes de géométrie. Mais pour cela, il faut comprendre dans ses très grandes lignes la géométrie projective, en admettant ses deux axiomes suivants :
- Par deux points distincts passe toujours une droite (et une seule).
- Deux droites distinctes se coupent toujours en un point (et un seul).
Le premier axiome, on le retrouve dans notre bonne vieille géométrie euclidienne, il ne va pas nous étonner. Par contre, le deuxième axiome a l'air manifestement faux, puisque deux droites parallèles ne se coupent a priori en aucun point. Mais ça, c'était avant : en géométrie projective, des droites parallèles se coupent quand même, mais en un point "à l'infini", sur la ligne d'horizon.
En fait, ces deux axiomes peuvent tout les deux se résumer sous la forme :
- Deux machins distincts se schtroumpfent toujours en un truc
Ces machins-trucs que sont les droites et les points sont en quelque sorte en dualité : en les inversant dans un axiome, on obtient l'autre.
Mais on peut faire encore plus fort. Partons de l'idée qu'un plan, c'est juste un ensemble de droites et des points. Alors on peut imaginer un nouvel espace où l'on appellerait "points" les droites du premier espace, et inversement (on se moque de savoir à quoi ressemble ce plan, ce n'est pas la question qui nous intéresse). Ce nouveau plan, on peut l'appeller "dual" du premier.
Mais ce plan dual vérifie toujours les deux axiomes de départ : il y a de bonnes raisons à le considérer comme un plan projectif comme les autres...
En fait, on peut mathématiser proprement la construction de ce plan projectif dual ; en le faisant, on s'aperçoit qu'il ressemble étrangement au plan de départ. Du coup, puisque ces objets passent au dual, on peut démontrer que les propriétés qui les définissent aussi.
Par exemple :
- Un point P du plan devient une droite (p) du dual ; une droite (d) du plan devient un point D du dual
- Dans le plan, deux droites (d) et (e) se coupent en un point P
=> dans le dual, deux points D et E forment une droite (p) - Dans le plan, trois points alignés P, Q et R forment une droite (d)
=> dans le dual, trois droites concourantes (p), (q) et (r) forment un point D

Une configuration du plan : trois droites (d), (e) et (f) concourantes en P, et trois points P, Q et R alignés sur (d).
La même configuration dans le dual : trois points D, E et F alignés sur (p), et trois droites (p), (q) et (r) concourantes en D.
Du coup, si un théorème de géométrie ne fait appel qu'à des notions d'alignements de points ou de concourances de droites, on peut les dualiser afin d'obtenir un nouveau théorème. C'est l'outil parfait pour doubler le nombre de théorèmes existants ! Place aux exemples !
Le théorème de Pappus
Parmi les théorèmes de géométrie injustement méconnus, il y a le théorème de Pappus (que l'on doit à Pappus d'Alexandrie) :
Théorème de Pappus :
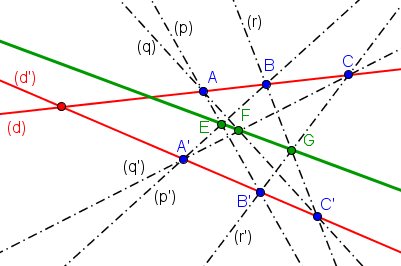
Soit A, B et C trois points distincts alignés sur une droite (d),
soit A', B' et C' trois points distincts alignés sur une droite (d'),
Notons (p)=(AB'), (p')=(A'B), (q)=(AC'), (q')=(A'C), (r)=(BC') et (r')=(B'C)
Alors, les points E = (p')∩(p'), F = (q)∩(q') et G = (r)∩(r') sont alignés
Ce théorème peut se dualiser, en inversant "droite" et "point", et en inversant "concourant" et "alignés". On obtient alors un tout nouveau théorème :
Théorème dual de Pappus :
Soit (a), (b) et (c) trois droites distinctes concourantes en un point D,
Soit (a'), (b') et (c') trois droites distinctes concourantes en un point D',
Notons P=(a)∩(b'), P'=(a')∩(b), Q=(a)∩(c'), Q'=(a')∩(c), R=(b)∩(c'), R'=(b')∩(c)
Alors, les droites (E) = (PP'), F=(QQ') et G=(RR') sont concourantes
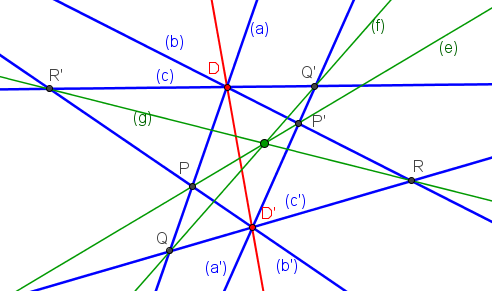
Ce théorème est loin d'être aussi élégant que son dual, mais il a le mérite d'exister. (Bon, en réalité, il décrit exactement la même configuration que dans le théorème de Pappus !...)
Le théorème de Desargues
Le théorème phare de la géométrie projective, c'est le théorème de Desargues, conséquence de celui de Pappus. On le doit au français Girard Desargues, que l'on peut considérer comme le père de la géométrie projective. Il indique :
Théorème de Desargues (*)
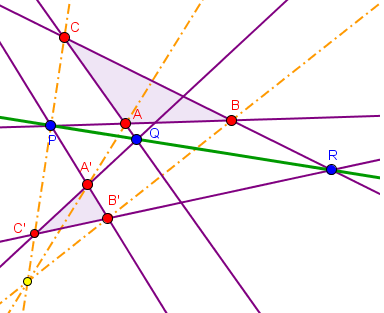
Soit deux triangles (non aplatis) ABC et A'B'C'
Si les droites (AA'), (BB') et (CC') sont concourantes
alors les points P = (AB)∩(A'B'), Q = (AC)∩(A'C') et R = (BC)∩(B'C') sont alignés
Encore une fois, le passage au dual permet de fabriquer un nouveau théorème. Enfin, presque nouveau, puisque ce n'est autre que la réciproque du théorème précédent. La seule différence est la surcomplexification inutile de son énoncé...
Réciproque du théorème de Desargues
Soit deux triangles (non aplatis) de côtés (a), (b) et (c), et de côtés (a'), (b') et (c')
Si les points (a)∩(a'), (b)∩(b') et (c)∩(c') sont alignés
alors les droites (p) = (ab;a'b'), (q) = (ac;a'c') et (r) = (bc;b'c') sont concourantes
(en notant (ab;a'b') la droite passant par ab=(a)∩(b) et a'b'=(a')∩(b'))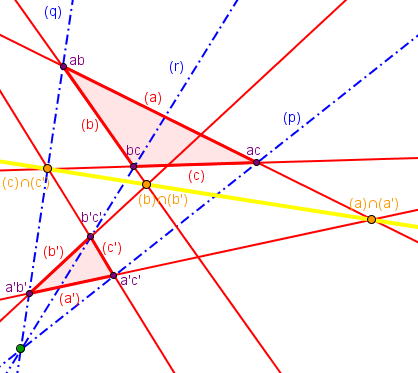
Le théorème de Pascal
Un autre théorème qui passe parfaitement au dual est celui de l'hexagramme mystique de Pascal, qui parle de coniques (ellipses, hyperboles, paraboles, ...) :
Théorème de Pascal
Soit A, B, C, A', B' et C' six points distincts sur une conique
Notons (p)=(AB'), (p')=(A'B), (q)=(AC'), (q')=(A'C), (r)=(BC') et (r')=(B'C)
Alors, les points E = (p)∩(p'), F = (q)∩(q') et G = (r)∩(r') sont alignés
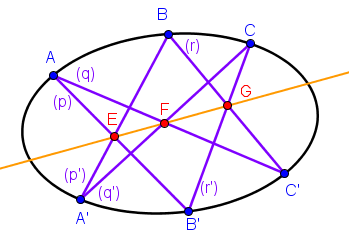
On peut voir que ce théorème est une généralisation de celui du théorème de Pappus, puisqu'un couple de droites n'est qu'un cas particulier de conique dégénéré.
L'hexagramme de Pascal peut également être dualisé, en ajoutant deux nouvelles correspondances entre le plan et son dual :
- Une conique dans le plan reste une conique dans le dual
- Un point sur une conique dans le plan devient une droite tangente à une conique dans le dual
Théorème de Brianchon
Soit (a), (b), (c), (a'), (b') et (c') six droites distinctes tangente à une conique
Notons P=(a)∩(b'), P'=(a')∩(b), Q=(a)∩(c'), Q'=(a')∩(c), R=(b)∩(c'), R'=(b')∩(c)
Alors, les droites (E) = (PP'), F=(QQ') et G=(RR') sont concourantes

Le théorème de Pascal est vrai quel que soit l'ordre des points A, B, C, A', B', C' que l'on considère. La droite orange obtenue dépend donc de l'ordre des points. Puisqu'il y a 60 façons de dessiner un hexagone à partir de 6 points, on peut obtenir une famille de 60 droites, les droites de Pascal. Cet énoncé passe au dual, ce qui entraîne l'existence de 60 points particuliers, les points de Kirkman (points de concourance des droites de Pascal).

(Une partie de) Les 60 droites de Pascal et les 60 points de Kirman
Oui, c'est n'importe quoi.
(*) Note de bas de page : à première vue, le théorème de Desargues n'est qu'un amas sans fond ni forme de points et de cercles. Pour le visualiser (et le mémoriser), on peut penser à cette figure : il faut imaginer que ABC et A'B'C' sont des coupes transversales parallèles d'une même pyramide. Ces coupes étant parallèles, les côtés se prolongent et se coupent deux à deux sur la même ligne d'horizon : ces points de concours sont donc alignés.
Sources :
Wikipedia, essentiellement
Pascal Lines, sur MathWorld