Quelle est la forme de l'Univers ?
Comment ça va ? Pourquoi le logo de France Télécom n'a pas d'accent ? Où est passé mon boitier à lunettes ? Jésus est-il ressuscité ? À quelle heure est-ce que tu rentres ? Qu'a fait votre gouvernement pendant 5 ans ? Pourquoi le poulet a traversé la route ? Quelle est la réponse à la grande question sur la vie, l'Univers et le reste ?...
Il y a des questions rhétoriques, d'autres qui demandent de vraies réponses réfléchies, il y a celles que l'on pose par flemme de chercher soi même la réponse... Et puis, il y a les questions fondamentales.
Pour continuer avec l'article topologique de la semaine dernière, j'ai envie d'apporter quelques éléments de réponses à cette question fondamentale : quelle est la forme de l'Univers ?
Quelle est la forme de la Terre ?
On peut déjà s'attarder sur la question de la forme de la (surface de la) Terre. La réponse qui nous intéresse aujourd'hui est la réponse topologique : est-ce plutôt un plan (avec ou sans bords), ou une plutôt une sphère, un tore ?
Avant le -IVe siècle, on penchait plutôt pour une Terre plate ou légèrement bombée. Un indice nous poussait à le croire : la surface de la Terre est une variété de dimension 2. Prenez un point de la terre et dessinez-y autour un cercle de 50 cm : si vous obtenez quelque chose qui ressemble à un disque, c'est que vous êtes sur une variété de dimension 2.
La topologie n'étant pas aussi développée qu'aujourd'hui, il a fallu attendre Aristote pour comprendre que toutes les variétés de dimension 2 ne sont pas homéomorphes au plan Euclidien (sans anachronisme...). Ce dernier a conjecturé, à raison, que la Terre était plutôt sphérique (en observant qu'un bateau qui s'éloigne à l'horizon ne devient pas de plus en plus petit, mais passe en fait en dessous de la ligne d'horizon)
Mais Aristote a écarté des hypothèse qui étaient alors encore vraisemblable : la Terre était peut-être un tore, un ruban, un ruban de Möbius, une bouteille de Klein ou des surfaces encore plus compliquées (puisqu'il existe un nombre infini de variétés de dimension 2 différentes).

Quelques variétés de dimension 2 : un plan, une sphère, un tore, un ruban de Möbius, un ruban, une bouteille de Klein et une surface encore plus compliquée (en l'occurrence, un double tore)
Finalement, puisque la Terre n'a pas de bord, c'est que ce n'est pas un ruban. C'est encore moins un ruban de Möbius, puisque le bateau de Magellan n'est pas revenu au Portugal à la maison en étant de l'autre côté de la lithosphère. L'hypothèse de la bouteille de Klein est difficilement concevable, puisque la Terre est plongée dans l'Univers (de dimension 3) sans auto-intersection. Reste deux hypothèses probables : la sphère ou le tore... On a très vite compris que la Terre était de genre 1, et qu'elle est donc une sphère...
Pour représenter les plus simples de ces variétés et les visualiser plus facilement, les topologues ont inventé une représentation par plan de montage. On part d'un domaine fondamental (typiquement, un carré), et on indique comment recoller deux à deux les côtés pour retrouver la variété recherchée. Pour l'exemple du tore, il faut recoller deux à deux les côtés opposés du carré fondamental en respectant leur sens : on commence par recoller ensemble deux côtés opposés pour obtenir un cylindre, et on colle les deux cercles opposés pour aboutir à un tore. Voici quelques plans de montages.

Différents plans de montages. Le cas de la sphère est à part, puisqu'il consiste à rétracter l'ensemble des points du bord en un seul. Le cas de la bouteille de Klein et du plan projectif donne des objets impossibles à monter dans un espace à 3 dimensions.
Ces représentations sous forme de carrés permettent de facilement géométriser ces surfaces : ça sera la bonne vieille géométrie euclidienne à Papa, où la somme des angles d'un triangle donne toujours 180°.
Quelle est la forme de l'Univers ?
Déterminer la forme de la Terre est finalement quelque chose de facile : il suffit de prendre une fusée et de la regarder de loin pour voir que c'est une sphère. C'est ici facile à faire, puisque la Terre fait partie de l'Univers (on va le supposer à 3 dimensions). Pour observer la surface de l'Univers, il faudrait pouvoir s'en extraire et le regarder depuis une 4eme dimension, ce qui est moins évident. Pour déterminer la forme de l'Univers, on ne dispose plus que d'une seul arme : l'observation.
Prenez un point de l'Univers, et déterminez l'ensemble des points qui sont situés à moins de 50 cm de ce point : si vous obtenez toujours une boule à 3 dimensions, c'est que l'Univers est une variété topologique à 3 dimensions (sans bords).
Reste plus qu'à choisir la bonne parmi l'infinité de variétés de dimensions 3 existantes. Il en existe une infinité... Mais les physiciens ont fait quelques observations qui vont permettre de limiter les possibilités. Selon l'uniformité du fond de rayonnement cosmologique (Je recopie telle quelle ma source, je n'ai aucune idée de la signification profonde de ces termes), la courbure de l'Univers ne varie pas, et le cosmos a une géométrie sphérique, hyperbolique ou euclidienne. À l'échelle de la Terre, Gauss a émis l'hypothèse que l'Univers est euclidien, en observant que la somme des angles d'un triangle formé par trois sommets de montagne donnait bien 180°.
On peut alors supposer que l'Univers est bien euclidien, ce qui simplifie bien les choses : il n'existe en effet que 18 variétés euclidiennes ! On peut même se restreindre à l'une des 10 variétés orientables ; les 8 autres entraineraient trop de conséquences encore jamais observées.
Un univers non orientable offrirait cependant de très bonnes idées aux scénaristes de science-fiction : après un voyage de quelques années autour de l'Univers, commandeur Cruise, soldat de la guilde spatial, revient sur la planète Terre, Celle-ci est totalement méconnaissable : les humains ont le cœur à droite, les horloge tournent dans le sens direct et les Anglais roulent à droite...
Espaces cubiques...
Pour visualiser les variétés tridimensionnelles, on peut utiliser le même artifice que pour les variétés bidimensionnelles, en prenant cette fois-ci un cube comme domaine fondamental. Suivant les cas, un parallélépipède quelconque peut faire l'affaire.
Le cas le plus simple (parmi ceux qui sont pas simples) à appréhender de cette façon est celui du tore tridimensionnel : quand on passe par l'un des côté du cube, on se retrouve de l'autre côté (sans changement de sens)
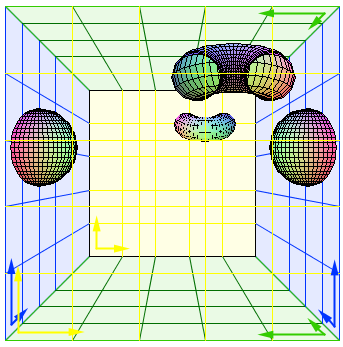
Cube (ou parallélépipède) fondamental du tore tridimensionnel. (1/10)
Quand la sphère ou le tore disparaissent dans un des côté, ils réapparaissent de l'autre.
Quand on se tient debout dans un tel Univers, on peut voir devant soi-même son propre dos (une infinité de fois, comme quand on place deux miroirs face à face), et on voit ses pieds en levant la tête !
Notons au passage qu'un Univers de cette forme a un volume fini, et l'expansion de l'Univers peut se traduire facilement par une expansion du cube.
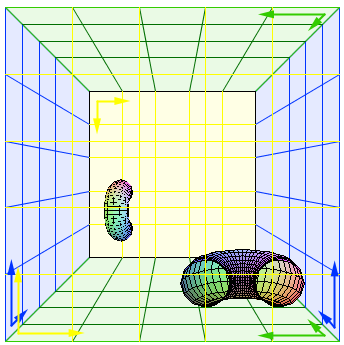
Mais on peut compliquer un peu plus, pour obtenir l'espace cubique demi-tour. On garde la même configuration pour quatre des six faces, mais les deux dernières seront recollées après une rotation de 180°. Ainsi, quand on se tient debout dans cet espace, on se voit de dos et la tête en bas....

Cube (ou parallélépipède) fondamental de l'espace cubique demi-tour (2/10)
À mi-chemin entre ces deux exemples, on trouve l'espace cubique quart de tour, où, cette fois-ci, la dernière face sera recollée avec seulement un quart de tour. Cette dernière face dans le parallélépipède fondamental doit être carrée.
Debout dans un tel espace, on se verrait juste devant à 90°, un peu plus loin à l'envers, encore un peu plus loin à 90° (dans l'autre sens)...
Cube fondamental de l'espace cubique quart de tour (3/10)
Espaces prismatiques...
Et si, au lieu de partir d'un cube, on part d'un prisme hexagonal ? Cela donne deux espaces nouveaux, appelés espaces prismatiques hexagonaux tiers de tour et sixième de tour.

Prismes fondamentaux des l'espaces prismatiques hexagonaux un tiers de tour (4/10) et un sixième de tour (5/10)
Suivant la direction où l'on regarde, on pourrait se voir simplement de dos, ou bien, de dos avec une rotation de 120° ou 60°...
Espace cubique double...
Le dernier des espaces de volume fini est l'espace de Hantze-Wendt. On ne part pas cette fois-ci d'un cube, mais de deux posés l'un à côté de l'autre. On fera correspondre simplement les faces de droite et de gauche (en vert). La face du fond à droite est identifiée à celle du fond à gauche après une réflexion d'axe horizontal (en jaune). La face du haut à gauche est collée à celle du bas à droite après une rotation de 180° (en rouge). On fait la même chose pour les faces en bleu.

Cubes fondamentaux de l'espace cubique double (6/10)
Ces 6 espaces sont les seuls espaces euclidiens sans bords orientables et de volume fini. Si vous pensez que l'Univers n'est pas infini (après tout, la Terre n'est pas un plan infini, pourquoi l'Univers lui aussi serait infini ?), il faut choisir parmi ces différentes topologies.
Et les 4 autres ?...
Les autres espaces euclidiens orientables sont de volume infini. Il y a bien évidemment l'espace ℝ3 (7/10), que l'on connaît parfaitement bien, puisque c'est celui dans lequel on a l'habitude de faire de la géométrie dans l'espace. Celui-ci est infini dans toutes les directions.
Mais il reste 3 espaces encore plus particuliers : les espace infinis dans seulement une ou deux directions. Les espaces infinis dans une seule direction sont les espaces de type "cheminée", et ressemblent à peu près à cela :
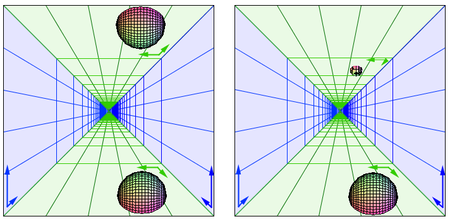
Domaines fondamentaux des espaces de type cheminée, direct (8/10) et indirect (9/10)
Pour obtenir ces espaces, on part d'une cheminée (un parallélépipède dont l'une des directions est infinie). Il reste alors deux paires de faces, qui sont des rectangles de largeur infinie. On peut recoller 2 à deux ces rectangles directement, ou bien faire d'abord agir une rotation d'angle 180°. On pourrait aussi sans problème faire faire agir des translations.
Il reste enfin un dernier espace : l'espace plaque (10/10). Le domaine fondamental que l'on prend est un domaine délimité par deux plans infinis parallèles. On recolle ensuite le premier plan sur le deuxième, en faisant comme bon nous semble une rotation ou une translation. L'espace que l'on obtient possède alors deux directions infinies, et une direction finie.
Le flambeau est désormais dans les mains des physiciens : c'est à eux de déterminer quelle est, parmi ces 10 formes possibles, celle de l'Univers. Si l'Univers est bel et bien euclidien (ou hyperbolique) et de volume fini, il existe loin dans l'espace un nombre infini de copie de notre galaxie : sa topologie n'est de toutes façon pas triviale. Si le domaine fondamental n'est pas trop grand (moins de 14 milliards d'années-lumière de rayon), il semble possible de découvrir sur notre voûte céleste une image de notre propre Voie lactée... Si le domaine fondamental est plus grand, ça va être un peu plus coton pour nous de le découvrir un jour...
Ca va bien, et toi ? - Pour acquérir une dimension internationale... De toute façon, ça s'appelle orange, maintenant - J'ai dû l'oublier dans la voiture, probablement - Ben oui, sinon, pourquoi mangerait-on du chocolat ? - J'arriverai un peu avant 20h - Je ne vous permets pas, monsieur Zemmour... - Pour aller de l'autre côté - 42.
Sources :
Dix autres mondes sont possibles, C. Adams, J. Shapiro - Pour la science n°308, juin 2003 (D'où provient l'illustration des prismes fondamentaux.)
