Clair de lune monstrueux
Halloween... Voici l'occasion de faire un article terrifiant sur un sujet effrayant !... Je pourrais le faire sur les nombres vampires, ces nombres comme 1395 qui gardent les mêmes chiffres une fois factorisés (par exemple, 1395=93x15). Je pourrais aussi parler des monstres de Poincaré, les courbes continues partout mais nulle part dérivables. Je pense aussi à l'escalier du diable, qui donne un exemple de variable aléatoire continue qui n'est pas à densité. Il y a aussi les spectres des opérateurs linéaires ou des anneaux commutatifs. Ou alors, je pourrais parler des courbes du diable, qui donnent des exemples de quartiques de genre 2... Mais il y a encore plus terrifiant... Il y a le...

En mathématiques, un groupe est un ensemble muni d'une loi de composition interne associative admettant un élément neutre et, pour chaque élément de l'ensemble, un élément symétrique. En gros, c'est une structure algébrique commode pour faire de la géométrie, ou pour décrire ce qui est possible dans les casse-têtes comme le Rubik's cube ou le taquin. C'est ce qui se cache dans la tête d'un mathématicien qui prononce le mot "symétrie".
Un exemple parmi beaucoup d'autre, c'est le groupe Z/5Z : l'ensemble des rotations qui conservent un pentagone. On peut en lister 5 : la rotation d'angle nul (l'élément neutre), celle d'angle 2π/5, celle d'angle 4π/5, celle d'angle 6π/5 et celle d'angle 8π/5. Deux transformations peuvent se composer de manière à en trouver une nouvelle, par exemple, effectuer à la suite deux rotations d'angle 2π/5, ça en fait une d'angle 4π/5. Ceci fait de cet ensemble un groupe. On peut représenter les éléments du groupe comme des permutations des sommets du pentagone (mais je ne sais pas si ça a un intérêt de le dire ici).
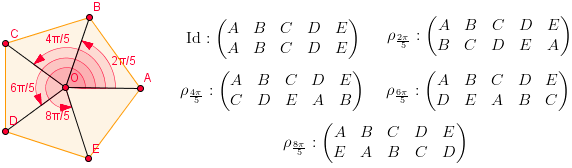
Interprétation géométrique du groupe Z/5Z, et ses 5 éléments
Autre exemple, le groupe D5 : l'ensemble des 10 transformations (affines) qui conservent un pentagone. Il est composé des mêmes rotations que précédemment, auquel on ajoute 5 symétries axiales.
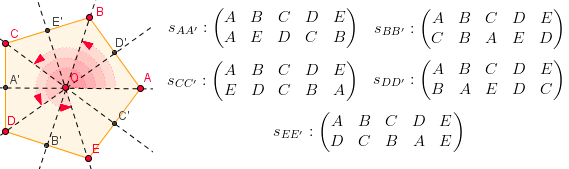
Interprétation géométrique du groupe D5 , et ses 5 autres éléments
Fait tout à fait intéressant : dans le groupe D5, on retrouve de manière assez naturelle le groupe Z/5Z (parmi les transformations du pentagone, on a entre autres les rotations). En langage mathématique, on dit que Z/5Z est un sous-groupe distingué de D5. Et on peut alors "diviser" le gros groupe par le plus petit, et le groupe D5 peut alors s'écrire comme un "produit" de deux groupes plus petits.
On distingue alors deux types de groupes : ceux qui sont simples, que l'on ne peut pas écrire comme un produit de deux groupes plus petits, et les autres. Les groupes simples sont les briques de bases du monde des groupes, de la même façon que les nombres premiers sont les briques des entiers, ou que les atomes sont les briques de la matières. Les groupes simples sont les atomes de la symétrie.
Dans les années 50, les mathématiciens du monde entier ont commencé à défricher cette jungle que sont les groupes finis. Plus d'une centaine s'y sont mis, produisant plus de 10 000 pages de démonstrations, pour arriver au théorème de classification que l'on connaît aujourd'hui.
Un groupe simple peut être :
- cyclique (qui correspondent à la géométrie du plan)
- alterné (qui interviennent dans le jeu du taquin)
- l'un des 42 types de groupes simples inconnus de l'étudiant en maths moyen : les 16 familles de groupes de type de Lie, ou les 26 groupes sporadiques (Ici, "sporadiques" signifie que quand on finit de décrire toutes les familles infinies de groupes, il en reste 26 qui ne rentrent nulle part).
Le plus petit de ces 26 groupes inclassable, c'est le groupe de Mathieu M11. Il possède tout de même 7920 éléments. On y croise aussi le groupe de Higman-Sims HS et ses quelques 44 352 000, qui représente les transformations d'un joli graphe à 100 points (Un graphe très esthétique, dont on peut retrouver plein de vues là-bas).
Mais le 26e, le plus gros de tous les groupes simples, possède pas moins de 808 017 424 794 512 875 886 459 904 961 710 757 005 754 368 000 000 000 (≈ 8 · 1053) éléments, et représente des transformations dans un espace à... ahem...196 883 dimensions... C'est celui que l'on appelle... le groupe monstre ! (et qui porte particulièrement bien son nom, compte tenu de sa monstruosité). Ce groupe a été découvert de manière théorique en 1973, et fabriqué de toutes pièces par Robert Griess au début des années 80.
En 1979, alors que John Conway et Simon Norton s'intéressaient aux fonctions modulaires, il ont vu sortir de nulle part le groupe monstre. C'est ce qu'ils ont appelé le...

En fait, tout commence avec John Mckay, qui découvre que le nombre 196 884 apparaît un peu partout en mathématiques, notamment dans la théorie des nombres (qui, a priori, n'a pas de rapports avec la théorie des groupes). Mais 196 883, c'est le nombre de dimensions dans lequel vit naturellement le Monstre. Quelque chose de bizarre se trame.
Cette coïncidence arrive jusqu'aux oreilles de Conway, qui décide d'enquêter.
D'un côté, il calcule les les représentations irréductibles du monstre, les dimensions dans lequel vit ce monstre. Il trouve :
1, 196883, 21296876, 842609326, 18538750076, 19360062527, 293553734298, ...
De l'autre, il calcule les coefficients du développement de Fourier de la fonction modulaire j (qui apparaît en théorie des nombres), et trouve :
1, 744, 196884, 21493760, 864299970, 20245856256, 333202640600, 4252023300096, 44656994071935, ...
La relation entre les deux saute aux yeux :
1 = 1
196884 = 1 + 196883
21493760 = 1 + 196883 + 21296876
864299970= 1 + 196883 + 21296876 + 842609326
...
Ce n'est définitivement pas un hasard. Conway et Norton écrivent alors ensemble en 1973 un papier qui prouve qu'il y a bien un lien entre les deux, sans que l'on sache vraiment pourquoi. Les questions laissées en suspens, ils appellent ça le "monstrous moonshine". Ici, le terme "moonshine" signifie essentiellement "complètement dingue", soit la première pensée de Conway quand on lui a dit qu'il y avait un lien entre le groupe monstre et les fonctions modulaires...
C'est lors d'une nuit de pleine Lune de 1998 que Richard Borcherds termine la démonstration de la conjecture de Conway-Norton, ce qui lui vaudra la médaille Fields en 1998. Pour les besoins de cette démonstration, il utilisera le...
(Nom qui fait référence au fait que le théorème parle de choses qui n'ont pas de vecteurs négatifs, de vecteurs fantômes. Mais aussi, parce que ça fait un jeu de mot absolument délicieux avec les "théorèmes no-go", les théorèmes qui établissent l'impossibilité physique de certaines situations)
Sources :
Wikipédia est une mine d'information sur la classification des groupes finis, du groupe monstre et du monstrous moonshine.
Le site de Mark Ronan offre une bonne vulgarisation de toutes ces considérations monstrueuses
