Réveillons le nombre d'or
"Une droite est dite coupée en extrême et moyenne raison quand,
comme elle est toute entière relativement au plus grand segment,
ainsi est le plus grand relativement au plus petit." [Euclide, Eléments, livre VI, 3ème définition]
Ainsi parla Euclide, et déjà, à l'époque, personne n'avait vraiment compris ce qu'il avait voulu dire. Depuis, de nombreux mathématiciens se sont penchés sur le sujet, et finalement, il parlait de ça :
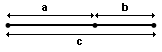
Un segment ayant ses proportions a/b et c/a égales.
Après mise en équation, en prenant c=a+b, on en arrive à l'équation : 
, que l'on peut aussi écrire 
Bref, ça donne quelque chose comme X²-X-1=0 (avec X=a/b), simple équation du second degré, dont la solution est : 
=
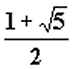, appellé "le nombre d'or". Le nom vient de Adolf Zeising, docteur en philosophie du XIXe siècle, qui s'était bien mis en tête de le chercher partout. On le note 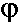(phi) en référence à Phidias, sculpteur grec, qui a décoré le Parthénon. Il vaut environ
1,618 033 988 749 894 848 204 586 834 365 638 117 720 309 179 805 762 862 135 448 622 705 260 462 189 024 497 072 072 041 (de mémoire...)
Reste cette question que l'on peut se poser : à quoi ça sert ? Pourquoi est-ce que je parle de ça ?
Et bien, ce rapport est joli. Enfin, c'est ce que pensent certains architectes, comme par exemple cet architecte moderne, qui a réalisé un temple suivant ces proportions :
(Le Parthénon)
A l'époque de Leonardo Di Caprio De Vinci, c'était plutôt ce que l'on appellait "la divine proportion" :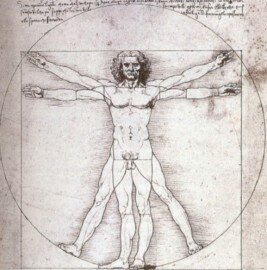
Un corps parfait semblerait posséder une certaine harmonie par rapport à .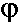
Mais ce n'est pas tout, la nature n'est pas en reste, voici un exemple, avec la spirale d'or, spirale inscrite dans un rectangle d'or (ses proportions sont égales au nombre d'or), et un reste de nautile.
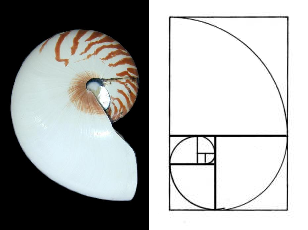
L'existence dans la nature de ce rapport est indubitable, celui de son existence dans l'art, par contre, est un peu plus discutable, mais on ne va pas renier le boulot de Zeising qui a passé sa vie à chercher ce nombre partout (forcément, quand on cherche, on trouve). Pour ce qui est de 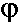comme critère de beauté, c'est, si je puis dire, un léger foutage de gueule...
Revenons-en alors à ses propriétés mathématiques. Vous vous rappellez sûrement de la suite de Fibonacci (Relisez la dernière note si vous ne vous en souvenez plus)
La suite, c'est quelque chose comme 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89...
Vous allez sûrement être épatés (encore plus si vous ne le saviez pas déjà), mais plus les nombres de cette suite sont grands, plus le rapport de deux nombres consécutifs se rapprochent du nombre d'or !
2/1 = 2
3/2 = 1.5
5/3 = 1.6667
8/5 = 1.6
13/18 = 1.625
21/13 = 1.6154
34/21 = 1.6190
...=
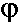1,6180
Épatant, non ?!
(En fait, si je vous ai parlé du nombre d'or, c'était juste pour en arriver à ce résultat, afin d'expliquer dans la prochaine note le pourquoi des nombres Fibonacci dans les tournesols, les ananas ou les callistemons)
Allez, et en cadeau bonus, quelques jolies égalités avec :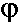
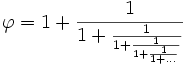
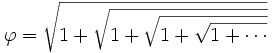
Documentation :
http://trucsmaths.free.fr/nombre_d_or.htm
http://pros.orange.fr/therese.eveilleau/pages/truc_mat/textes/rectangle_dor.htm
http://fr.wikipedia.org/wiki/Nombre_d'or