Conjecturons, mais pas trop vite
La conjecture le théorème des quatre couleurs (Formulé en 1852, démontré de manière satisfaisante en 2006), la conjecture de Kepler le théorème de Hales (Formulé en 1611, apparemment résolu en 2003), la conjecture de Fermat le théorème de Wiles (Formulé en 1670, démontré en 1995), la conjecture de Poincaré le théorème de Perelman (Formulé en 1904, démontré en 2003)...
Une conjecture, c'est un résultat mathématique que l'on espère vrai, mais pour lequel personne n'a jamais pu trouver de démonstration. Et quand une démonstration tombe après une longue attente, c'est champagne ! Tout le monde sort dans la rue, avec confettis, chapeaux pointus et langues de belle-mère !
Mais quand après une longue attente, on s'aperçoit que la conjecture est complètement nulle, c'est la grande déception... Rendons donc aujourd'hui hommage aux conjectures les plus foireuses !
La conjecture de Borsuk
"Tout compact convexe de dimension n peut être découpé en n+1 parties de diamètre plus petit". En 1932, après avoir démontré le théorème pour les sphères de dimension n, Borsuk posa cette question de géométrie discrète.
Pour comprendre ce que signifie l'énoncé de Borsuk, prenons le cas n=2 du plan, avec la patatoïde orange suivante. Cette patatoïde est compacte (son dessin ne dépasse pas le cadre) et convexe (deux points à l'intérieur peuvent toujours être reliés par un segment sans sortir). Le diamètre correspond à la longueur entre les deux points les plus éloignés de la patatoïde.
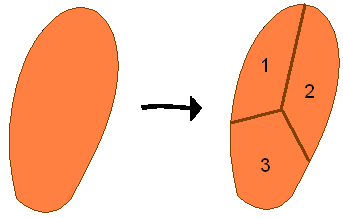
Dans ce cas, on peut bien découper l'objet en 3 parties de plus petits diamètres. (et même en deux morceaux, en fait). En prenant un triangle équilatéral, il aurait fallut trois morceaux. On peut facilement s'imaginer des exemples dans le cas d'un objet en volume pour la dimension trois découpé en 4 morceaux.
Jusqu'en 1993, on ne se pensait pas à l'existence d'un contre exemple, surtout que des résultats intermédiaires ont pu être démontré. Le contre-exemple, découvert par Kahn et Kalai, porte sur un objet de dimension... 1325 !
Pour faire une bonne conjecture, il faut une bonne intuition... Apparement, Borsuk n'avait pas celle de la 1325e dimension !
La conjecture d'Euler
Passons à un mathématicien bien plus renommé, avec une conjecture plus abordable : Histoire de généraliser la conjecture de Fermat, Leonhard Euler proposa (en 1769) sa propre conjecture :
Pour tout n>2, on ne peut trouver n-1 entiers tels que la somme de leur puissance n-ième soit une puissance n-ième.
Autrement dit : on ne peut trouver d'entiers (a1, ..., an-1, b) tels que a1n+...+an-1n=bn .
C'est en 1966 que le couperet tomba : un contre exemple fut découvert (par L. J. Lander et T. R. Parkin), pour n=5 :
275 + 845 + 1105 + 1335 = 1445
En 1988, Elkies propose même un moyen de trouver autant de contre-exemple que l'on veut pour n=4, le plus petit obtenu par sa méthode est le suivant :
2 682 4404 + 15 365 6394 + 18 796 7604 = 20 615 6734
Euler a conjecturé qu'il n'y a avait aucune solution, Elkies a montré qu'il y en avait une infinité... Zut !
La conjecture de Fermat (l'autre)
La conjecture de Fermat (1670), c'est "si n>2, on ne peut trouver d'entiers a, b et c tels que an+bn=cn ". C'est aujourd'hui un théorème, et la voie de sa résolution a amené bien des avancées en mathématiques !
La conjecture de Fermat (l'autre, en 1640), c'est "Pour tout n, 22n+1 est un nombre premier" ! Mais cette conjecture ira moins loin que sa grande sœur.
Pierre de Fermat avait déjà étudié les nombres de la forme 22n+1 (Aujourd'hui appelés nombres de Fermat), en remarquant notamment que si un nombre de la forme 2k+1 est premier, alors k est une puissance de 2. Les petits n allaient dans le sens de la réciproque :
n=0 : F0 = 21+1 = 3 (premier)
n=1 : F1 = 22+1 = 5 (premier)
n=2 : F2 = 24+1 = 17 (premier)
n=3 : F3 = 28+1 = 257 (premier)
n=4 : F4 = 216+1 = 65637 (premier)
Avec les 5 premiers termes premiers, on a de quoi s'attendre à ce que les termes suivant le soient , d'où la conjecture de Fermat.
Jusqu'à ce que Euler s'en mêle, et montre (en 1732) que F5 est un nombre composé ! (F5 = 641 × 6 700 417)
Puis Landry (1880) montre que F6 est composé !
Aujourd'hui, on sait que de tous les nombres de Fermat entre F5 et F32, aucun ne sont premiers !
Fermat pensait que ses nombres étaient tous premier, on a tendance à conjecturer qu'il n'y en a pas d'autre !



/http%3A%2F%2Fstorage.canalblog.com%2F39%2F29%2F210892%2F122373793_o.png)
/https%3A%2F%2Fassets.over-blog.com%2Ft%2Fcedistic%2Fcamera.png)
/http%3A%2F%2Fstorage.canalblog.com%2F53%2F54%2F210892%2F92246854_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F85%2F70%2F210892%2F65561362_o.png)