2015+1 (Cette nouvelle année est-elle intéressante ? Episode 07)
Une nouvelle année débute ! Je n'ai pas réellement abandonné ce blog, je suis simplement sur un projet plutôt chronophage... Mais je ne vais pas abandonner ma tradition annuelle : zieuter l'OEIS à la recherche des propriétés du nombre correspondant à l'année commençante.
Chaque année, je revêts donc mes plus beaux habits d'arithmomancien, afin de donner mes prédictions sur l'année qui arrive. Au contraire d'une Elisabeth Tessier affirmant que "la Vénus de la France, à 3° Balance [...] est en dissonance avec le thème de Daech, créé le 28 juin 2014, dans le premier décan du Cancer" pour expliquer les attentats de novembre, l'arithmomancie est une pratique divinatoire sans risque, puisqu'elle ne se risque à aucune prédiction concrète. En janvier dernier, j'affirmais sur ce blog que l'année 2015 allait être intéressante, et elle l'a été [référence nécessaire] . Qu'en est-il de 2016 ? Ouvrons pour cela l'encyclopédie en ligne des suites entières (OEIS).
Rappelons tout de même que si une suite de nombres (entiers) est intéressante, elle sera présente dans cette encyclopédie. Ainsi, plus un nombre possède des propriétés intéressantes, plus il apparaît dans l'OEIS.
Les nombres 2013, 2014 et 2015 possèdent donc (au moment où j'écris cet article) respectivement 111, 106 et 179 propriétés intéressantes. Et 2016, dans tout ça ?... Eh bien...
2016 possède 783 propriétés intéressantes !
C'est absolument indubitable : l'année 2016 sera intéressante ! C'est même l'année la plus intéressante depuis (au moins) 100 ans, et pour les 100 ans à venir (à l'exception de 2048, mais j'en reparlerai dans 32 ans) ! Voyons un peu quelques raisons.
2016 est un nombre triangulaire [A000217]
Premier point important, 2016 est un nombre triangulaire, ce qui signifie que 2016 points peuvent être représentés comme ça :
Plus précisément, on dit qu'un nombre est triangulaire si on peut l'écrire sous la forme 1+2+3+4+...+N (la forme triangulaire vient du fait que la 1ere ligne compte 1 point, la seconde 2 points, etc.). Les premiers nombres triangulaires sont donc 1, 3, 6, 10, 15, ....
Avec N=63, cela correspond à l'égalité 1+2+3+...+63 = 2016.
Puisqu'il est question de nombre triangulaire, il convient de rappeler la légende autour de l'enfance du mathématicien Carl Friedrich Gauss. Alors qu'il était âgé de 9 ans, son professeur lui aurait demandé de calculer de tête la somme 1+2+3+...+100, pensant avoir la paix durant de nombreuses minutes. Ce n'est qu'après quelques secondes que le jeune Gauss aurait répondu 5050. En fait, avec un petit raisonnement, on peut retrouver très facilement ce résultat, en formant des paires de nombres. En effet, on peut voir que 1+100=101, 2+99=101, 3+98=101, et ainsi de suite, si bien que avec les nombres de 1 à 100, on peut former 50 paires de cette forme. Cela donne finalement 50×101=5050.
Il est assez amusant de découvrir que cette histoire a progressivement évolué de biographies en biographies de Gauss, l'histoire originale ne mentionnant jamais ces nombres de 1 à 100. Dans son article Gauss's Day of Reckoning, Brian Hayes recense plus d'une centaine de versions différentes de cette même histoire !
On peut tout de même appliquer cette méthode de Gauss pour prouver que 1+2+3+...+63 = 2016. En effet, on a 1+63=64, 2+62=64, et ainsi de suite. Dans la somme 1+2+3+...+63, on peut retrouver 31 paires dont la somme vaut 64, ce qui donne 31×64=1984. Il reste à ajouter 32, le terme central de la somme (qui n'a pas été pris en compte lors des paires), ce qui donne finalement 1984+32=2016.
En généralisant le raisonnement, on peut prouver que 1+2+3+4+...+N = N/2×(1+N). Une démonstration assez classique "sans mot" de cette formule repose sur la figure suivante :
Une autre façon de retrouver les nombres triangulaires est de passer par le triangle de Pascal, un triangle formé de nombres contruit de façon à ce que chaque terme soit la somme des deux au-dessus. Par construction, on retrouve sur la troisième diagonale la suite des nombres triangulaires.

Le triangle de Pascal, construit de façon à ce que chaque nombre soit la somme des deux juste au-dessus (à titre d'exemple, 15+6=21, en rose)
La troisième diagonale, en bleue, correspond donc à des nombres de la forme 1+2+3+4+...+N : les nombres triangulaires.
On retrouvera donc 2016 dans la 64e ligne du triangle de Pascal.
Les nombres que l'on retrouve dans le triangle de Pascal peuvent être interprétés d'une façon combinatoire : le nombre que l'on retrouve sur la n-ème ligne et k-ième colonne est le nombre de façons de choisir k objets parmi n possibles. Ainsi, 2016 est le nombre de façons de choisir 2 objets parmi 64.
On peut alors interpréter ce résultat en disant que 2016 est :
- Le nombre de façons de placer deux cavaliers sur un échiquier (cela correspond à choisir 2 cases parmi les 64)
- Le nombre d'arêtes d'un graphe complet à 64 sommets (chaque arête correspond au choix de 2 sommets parmi les 64), ce qui donne visuellement ceci :
2016 est un nombre hexagonal [A000384]
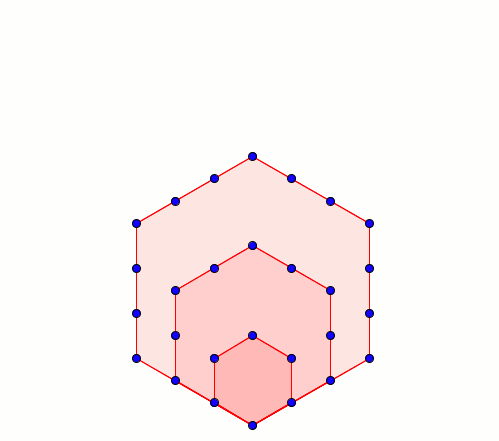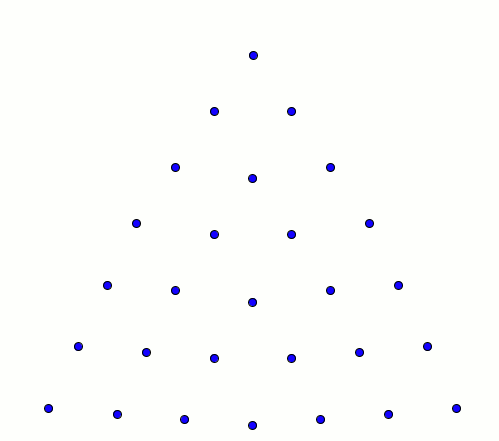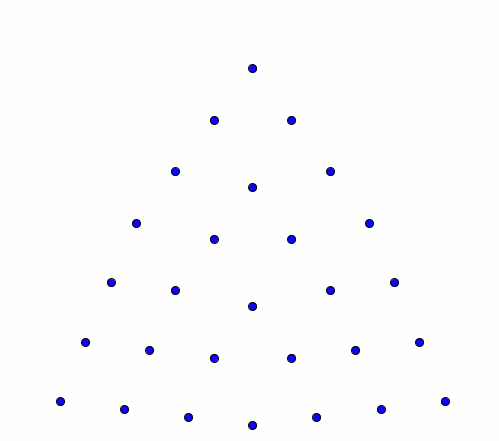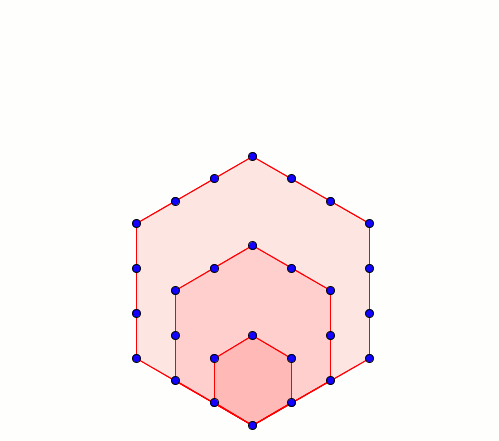
Mais 2016, c'est aussi un nombre hexagonal, ce qui visuellement donne ceci :

2016 fera vraiment mal aux yeux.
Chose intéressante : les nombres hexagonaux sont toujours des nombres triangulaires. On peut bien sûr le prouver algébriquement, mais j'espère que cette petite animation saura être plus parlante :
A noter que tous les nombres triangulaires ne sont pas pour autant hexagonaux.
On peut aussi dire que 2016 est un nombre icosikaitetragonal, puisqu'il peut être représenté sous la forme de polygone à 24 côtés [A051876] ...
2016 est un nombre presque parfait [A006516]
2016 peut s'écrire sous la forme 2016 = 25(26-1). Grâce à cette propriété, cela fait de 2016 le nombre de diagonales d'un hypercube de dimension 6. Mais ce qui est encore beaucoup plus intéressant avec cette écriture, c'est que cela correspond parfois à des nombres parfaits.
Un nombre parfait, c'est un nombre égal à la somme de ses diviseurs propres. Le nombre 28 en est un bon exemple : ses diviseurs (propres) sont 1, 2, 4, 7 et 14, et on a l'égalité 1+2+4+7+14=28.
On sait facilement construire des nombres parfaits (relaté par Euclide dès le IIIe siècle avant JC) : si le nombre 2p-1 est un nombre premier, alors le nombre 2p-1(2p-1) sera un nombre parfait. Pour obtenir 28, il suffit de voir que 23-1=7 est premier, et donc que 22 (23-1) = 28 est parfait. Réciproquement, on peut prouver que dès qu'un nombre pair est parfait, alors on pourra l'écrire sous la forme 2p-1(2p-1) avec 2p-1 premier.
Des nombres premiers de la forme 2p-1, on en connaît pas mal : 3, 7, 31, 127... Depuis 2013, on connaît 48 nombres premiers de cette forme, si bien que l'on connaît aujourd'hui 48 nombres parfaits. Ces nombres premiers de la forme 2p-1 sont ce que l'on appelle les nombres premiers de Mersenne : ils ont un intérêt tout particulier en maths, puisqu'ils fournissent les plus grands exemples de nombres dont on peut être sûr et certain qu'ils sont bien des nombres premiers. Le plus grand d'entre eux est 257 885 161-1, et compte tout de même 17 425 170 chiffres (voir là). [Mise à jour du 07/01 : on compte en fait 49 nombres parfaits, puisqu'un nouveau nombre de Mersenne premier vient d'être découvert, il s'agit de 274,207,281-1, qui compte 22 338 618 chiffres]
Les nombres parfaits gardent encore pas mal de mystères. A l'heure actuelle, on ne peut aucunement connaître le nombre de nombres parfaits qui existent.
D'un côté, il y a les nombres parfaits pairs, liés aux nombres premiers de Mersenne. Puisqu'on ne sait pas s'il existe ou non un nombre infini de nombres premiers de Mersenne, on ne peut rien dire non plus pour les nombres parfaits pairs.
De l'autre côté, il y a les nombres parfaits impairs. Là, c'est encore pire : on peut dire de nombreuses choses à leur sujet (un nombre parfait impair doit avoir plus de 1500 chiffres ou ne pas être divisible par 105, par exemple), mais le principal reste à démontrer, puisqu'on ne sait pas si des nombres parfaits impairs existent bel et bien.
Bon, par contre, 2016 peut s'écrire sous la forme 2016=25(26-1). Or, 26-1=63, ce qui n'est pas un nombre premier, donc 2016 n'est pas un nombre parfait...
2016 appartient à la "suite des cabines téléphoniques" [A192008]
En cherchant un peu, on trouve aussi des propriétés beaucoup moins utiles. Cette situation, par exemple :
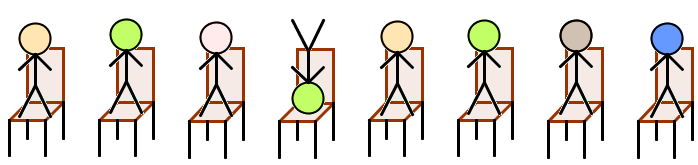
Imaginons la salle d'attente d'une administration quelconque où sont disponibles seulement 8 chaises, toutes les unes à côté des autres. Successivement, 8 personnes vont arriver dans cette pièce (et aucune ne partira avant que la pièce ne soit remplie). Lorsqu'une personne entre dans la pièce pour venir s'asseoir, elle veillera toujours à maximiser son confort personnel. Pour cela, elle ne s'installera jamais à côté d'une place déjà occupée, sauf si ces places sont les seules disponibles (dans ce cas, une place ne possédant qu'un seul voisin sera toujours préféré à une place à 2 voisins).
Ainsi, le premier arrivant aura le choix entre 8 chaises. Imaginons qu'il prenne la troisième.
Les chaises 2 et 4 sont maintenant indisponibles (trop proche d'une place occupée), la deuxième personne à entrer pourra choisir entre la chaise 1, 5, 6, 7 et 8. Disons qu'elle prend la 7eme.
A présent, seules deux chaises sont encore disponibles (la 1 et la 5). Les deux prochains qui entreront choisiront donc ces deux chaises.
Une cinquième personne arrive. Parmi les 4 chaises restantes, toutes ont deux voisins, sauf la dernière. C'est donc vers cette dernière que le nouvel arrivant se dirigera.
Les trois derniers qui arriveront n'auront plus la possibilité d'obtenir des places tranquilles. Ils se partageront donc les trois dernières places restantes.
Les chaises ont donc été choisies selon l'ordre 3, 7, 1, 5, 8, 2, 4, 6, ce qui ne représente en fait que l'une des 2016 façons de remplir toutes ces places !
- Un carré magique de taille 8×8 composé uniquement de nombres premiers a au minimum 2016 comme constante magique. [A073520]
- Il existe 2016 matrices 2×2 inversibles dans ℤ/7ℤ. [A000252]
- On peut compter 2016 cellules 5D dans un hypercube de dimension 9. [A054849]
- Le déterminant de la matrice suivante est -2016. [A092415]
En fait, la principale raison pour laquelle 2016 possède autant de propriétés, c'est que 2016 possède énormément de diviseurs (il en possède 36 : 1, 2, 3, 4, 6, 7, 8, 9, 12, 14, 16, 18, 21, 24, 28, 32, 36, 42, 48, 56, 63, 72, 84, 96, 112, 126, 144, 168, 224, 252, 288, 336, 504, 672, 1008, 2016). Des nombres avec autant de diviseurs, c'est plutôt rare, et cela explique sa surreprésentation dans l'OEIS. Puisque, en plus, c'est un nombre triangulaire, cela lui rajoute de nombreuses propriétés dérivées.
Bref : que cette année 2016 soit la plus intéressante pour vous.
Et surtout, la santé !













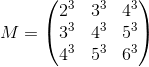

/http%3A%2F%2Fstorage.canalblog.com%2F54%2F29%2F210892%2F128353700_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F97%2F87%2F210892%2F113994993_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F72%2F15%2F210892%2F107004083_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F98%2F97%2F210892%2F92096273_o.png)