2014+1 (Cette nouvelle année est-elle intéressante ? Episode 06)
Une nouvelle année commence, avec son lot de bonnes résolutions qui ne seront pas tenues. Par exemple, j'ai décidé, en cette nouvelle année, d'écrire enfin un article sur Maryam Mirzakhani ! Vais-je tenir cette bonne résolution ?...
En tout cas, il y a une coutume à laquelle je ne résiste pas : éplucher l'OEIS à la recherche des propriétés intéressantes du nombre correspondant à l'année qui débute. Que peut-on dire de 2015 ? Je me tourne une nouvelle fois vers l'arbitre officiel de ce qui est intéressant : l'OEIS.
Rappelons que l'OEIS est l'encyclopédie en ligne des suites entières. Si une suite de nombres (entiers) est intéressante, elle sera présente dans cette encyclopédie. Du coup, si un nombre possède une propriété intéressante, elle sera dans une suite intéressante, et donc, dans l'OEIS. Ainsi, plus un nombre apparaît dans l'OEIS, plus il pourra être considéré comme intéressant.
Les nombres 2012, 2013 et 2014 possèdent donc (au moment où j'écris cet article) respectivement 131, 104 et 88 propriétés intéressantes. Et 2015, dans tout ça ?... Eh bien...
2015 possède 170 propriétés intéressantes !
2015 sera-t-elle enfin l'année où la courbe va s'inverser ? A en croire l'OEIS, oui !..
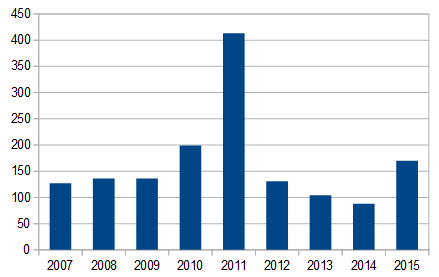
Nombre de propriétés pour chaque année, selon l'OEIS
Mais voyons dans le détail ce que l'OEIS nous dit de 2015...
Arbre de diamètre 5 [A189979]
Dans un graphe, le diamètre est la plus longue distance séparant deux sommets. Par exemple, les deux graphes suivants ont pour diamètre 5 :
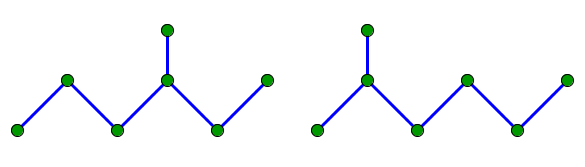
La distance séparant deux sommets dans un de ces graphe est toujours inférieure ou égale à 5.
Ces deux graphes ne sont pas simplement des graphes : ce sont des arbres (ils ne possèdent aucune boucle - ou cycle). Et on peut en fait vérifier que ce sont les deux seuls arbres de diamètre 5 possédant 7 sommets.
On peut aussi vérifier qu'il existe 7 graphes de diamètre 5 possédant 8 sommets :
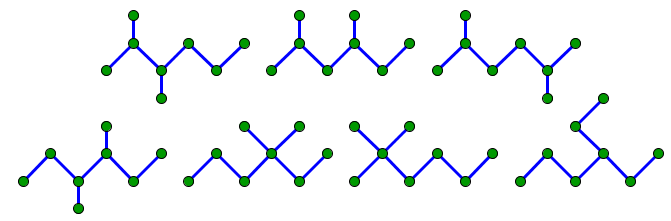
Et pour les graphes de diamètre 5 possédant 18 sommets, il y en a 2015 :

Un exemple parmi les 2015 existants...
Sous-réseaux tridimentionnels [A001001]
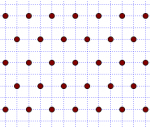
Les points à coordonnées entières dans le repère d'un plan (infini) forment ce que l'on appelle un réseau carré.
En sélectionnant ces points de façon adéquate (en ne gardant que 1 sur 2, ou que 1 sur 3, toujours de la même façon), on forme un sous-réseau. On dira que le sous-réseau est d'ordre n si on en a gardé que 1 sur n.
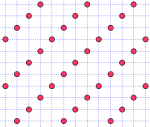
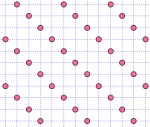
Ainsi, on peut fabriquer exactement 7 sous-réseaux carrés d'ordre 4, suivant la façon dont on sélectionne "un point sur 4" :
On peut en fait démontrer que le nombre de sous-réseaux carrés d'ordre n est égal à σ(n), c'est à dire, la somme des diviseurs de n. Puisque les diviseurs de 4 sont 1, 2 et 4, σ(4) = 1+2+4 = 7, ce qui est bien le nombre de sous-réseaux carrés d'ordre 4. On peut ainsi vérifier qu'il y a 6 sous-réseaux carrés d'ordre 5, et 12 d'ordre 6. Mais tout ceci n'a rien a voir avec 2015.
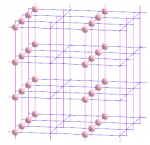
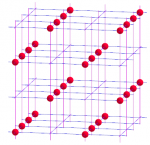
On peut de la même façon chercher les sous-réseaux d'un réseau cubique, à 3 dimensions (les points à coordonnées entières dans un repère de l'espace). Pour ce qui est des sous-réseaux cubiques d'ordre 2, on en dénombre 7 différents :
Le nombre de sous-réseaux cubiques d'ordre n est en fait donné par la formule
On peut ainsi vérifier que le nombre de sous-réseaux cubiques d'ordre 3 est 13, mais surtout, que le nombre de sous-réseaux cubiques d'ordre 24 est... 2015 !
Triangles rectangles distincts [A189979]
Prenons une grille 4x4 : combien peut-on y tracer de triangles rectangles différents, à une isométrie (translation, symétrie, rotation) près ?
La réponse en gif est 9 :

Et sur une grille 40x40 ?... 2015, évidemment !
Mais 2015 possède d'autres propriétés intéressantes !
- [A129868] 2015, quand on l'écrit en binaire, devient 11111011111 : c'est un palindrome ! (Voir l'article de Blogdemaths pour une étude détaillée de ces nombres palindromes)
- [A006972] 2015 est un nombre de Lucas-Carmichael. Ces nombres ont une définition proche de celle des nombres de Carmichael, qui sont les nombres qui ont l'air premier au yeux du test de primalité de Fermat (le plus classique des tests de primalité), mais qui ne le sont en fait pas du tout. Mais comme ils n'ont pas la même définition, les nombres de Lucas-Carmichael n'ont en fait aucun intérêt (sinon celui d'exister, et ça, c'est cool)
Un nombre n, donc, est appellé nombre de Lucas-Carmichael lorsque : si p est un facteur premier de n, alors p+1 divise n+1 (il faut en plus que n soit sans facteur carré)
2015 possède 3 facteurs premiers, qui sont 5, 13 et 31. Puisque les nombres 6, 14 et 32 sont des diviseurs de 2016, alors 2015 est un nombre de Lucas-Carmichael. - [A001304] Il y a 2015 façons différentes de composer un bouquet fleurs à 45 € chez un fleuriste proposant 4 types de fleurs coûtant respectivement 1, 1, 2 et 5 €.
- [A164576] 2015 est la moyenne des 77 premiers carrés : 2015 = (1²+2²+3²+...+77²) / 77
- [A115160] 2015 ne peut pas être écrit comme la somme de deux nombres triangulaires et d'un nombre à la puissance 4.
- [A124189] Le nombre 1 + 2015 + 20153 + 20155 + 20157 + 20159 + 201511 + ... + 201539 est un nombre premier ! (Un point à celui qui arrive à replacer ça dans une conversation)
- [A120828] Le nombre 109876543210987...109876543210987 (qui compte 2015 chiffres) est un nombre premier ! (Un point bonus à celui qui arrive à replacer ça en plus dans la même conversation)
Et quelques autres propriétés glanées sur Twitter aux alentours du 1er janvier :
- 2015 = 48×48-17×17 ! Mais si vous avez trop bu et que vous lisez à l'envers, 84×84-71×71, ça fait toujours 2015. (@MickaelLaunay)
- 2015 = 13³-13²-13¹ (@brusicor02) [A152015]
Et la santé !










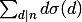

/http%3A%2F%2Fstorage.canalblog.com%2F72%2F92%2F210892%2F113119539_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F00%2F91%2F210892%2F107069165_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F83%2F38%2F210892%2F101168363_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F13%2F67%2F210892%2F100586073_o.jpg)