2012+1 (Cette nouvelle année est-elle intéressante ? Episode 04)
Que doit-on attendre de cette nouvelle année à venir ? L'argent ? L'amour ? La santé ? Comme il est de coutume sur ce blog, nous allons répondre à cette épineuse question par la pratique ce difficile art divinatoire consistant à lire l'avenir dans l'OEIS. Cette encyclopédie regroupe aujourd'hui plus de 200 000 listes, de la suite de Fibonacci à [A000045] à la suite des coefficients du développement en série entière de x(1+x+x2)/[(x-1)(x3+x2-1)] [A171861]. Pour savoir si l'année 2013 sera intéressante, il suffit de regarder le nombre d'apparitions du nombre 2013.
Ainsi, l'année 2011 était très intéressante, puisque 2011 a 363 propriétés intéressantes. Par exemple, 2011 est un nombre premier p qui n'est pas de Ramanujan tel que ]p, 2q] (où q est le plus petit nombre premier supérieur à p/2) contient au moins un nombre premier [A164368] !...
L'année 2012 était beaucoup moins intéressante : seulement 113 propriétés. Parmi celles-ci, on peut constater que le numérateur de 1+1/2+1/3+1/4+...+1/2012 est un nombre premier (A056903).
Et 2013, dans tout ça ? L'année qui arrive sera-t-elle passionnante ou déprimante ? Le grand amour frappera-t-il à votre porte ? Si oui, va-t-il se barrer en courant ? Suspens...
2013 ne possède que 90 propriétés !
Il faut voir la vérité en face : la crise des propriétés qui a débuté l'année dernière se prolongera cette année... Avant de se passer la corde au cou, détaillons-en quelques-unes.
Arbres à 4 feuilles [A055291]
En combinatoire, on aime bien les arbres. Mais ce qu'on aime encore plus, c'est compter les arbres.
Tiens, par exemple, combien existe-t-il d'arbres à 5 branches (et donc, à 6 sommets) ?
Six. Il existe 6 arbres à 5 branches.
En détaillant un peu plus, on compte :
à 2 feuilles : 1 arbre
à 3 feuilles : 2 arbres
à 4 feuilles : 2 arbres
à 5 feuilles : 1 arbre
Et pour les arbres à 26 branches comme celui-ci ?
Un arbre à 26 branches et 4 feuilles parmi tant d'autres.
Des arbres à 26 branches (et 27 noeuds), il en existe 751 065 460. Mais le plus intéressant, c'est qu'il y en a exactement 2013 qui possèdent 4 feuilles !
Nombre de Smith [A104390]
Prenez le nombre 4937775. Sa décomposition en facteurs premiers est 4937775=3×5×5×65837. Ce nombre est tout à fait fascinant, puisque la somme S de ses chiffres (4+9+3+7+7+7+5=42) est égal à la somme Sp des chiffres de ses diviseurs premiers (3+5+5+6+5+8+3+7=42). Un tel nombre a été baptisé "nombre de Smith" par l'américain Albert Wilansky, en l'honneur de son beau frère Harold Smith dont le numéro de téléphone était 493-7775.
Il existe 376 nombres de Smith inférieurs à 10000 (on exclut les nombres premiers de la définition). Parmi eux, le nombre 666=2×3×3×37, puisque S(666)=6+6+6=18 et Sp(666)=2+3+3+3+7=18.
Et 2013, dans tout ça ? La décomposition en facteurs premiers de 2013 est 2013=3×11×61. En sommant les chiffres, on trouve :
S(2013) = 2+0+1+3 = 6
Sp(2013) = 3+1+1+6+1 = 12 (= 2×6)
2013 n'est donc pas un nombre de Smith, mais un nombre de 2-Smith : les chiffres de sa décomposition valent le double de ses chiffres. De manière générale, un nombre N composé est un nombre de k-Smith si Sp(N)=k.S(N).
Il a été montré qu'il existe une infinité de nombres de k-Smith, quelque soit k et la base b>2 considérée. La question de la finitude des nombres de k-1-Smith reste cependant encore à trancher.
Règle 942 [A169649]
Le roi des automates cellulaires, c'est le jeu de la vie : une grille infinie et quelques règles à suivre régissant la vie ou la mort des cellules, étapes après étapes. Pour l'automate qui nous intéresse (celui défini par la règle 942 de Wolfram), il n'y a qu'une seule règle à suivre : si une cellule est voisine de 1 ou 4 cellules activées, elle sera activée à l'étape suivante. A l'étape 1, une seule cellule est activée.
Les premières étapes ressemblent alors à :
Les 6 premières étapes de cet automate cellulaire
La 34e étape est moins esthétique, mais elle comptera 2013 cellules activées !
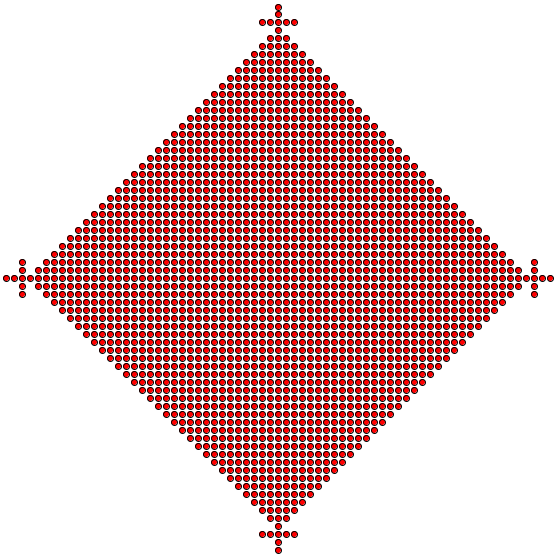Attention, ne pas fixer trop longtemps cette image sous peine de céphalées sévères.
Mais 2013 a d'autres propriétés intéressantes :
- 2013 et ses deux entiers successeurs possèdent exactement trois diviseurs premiers [A066509, A113789, A113789]. Du coup, d'autres propriétés en découlent : ils ont le même nombre de diviseurs (ils en ont 8) [A005238], ils ont la même signature [A052214]
- 2013 est le produit de trois nombre premiers tels que la somme du carré de ces nombres est aussi un nombre premier. En effet, 2013 = 3×11×61, et 3²+11²+61²=3851 est un nombre premier [A176878].
- 2013 est un nombre allitératif (en anglais) : chaque mot commence par la même lettre (t) [A146755].
- A priori, une puissance de 2 écrite en base 3 ne peut pas avoir 2013 zéros [A036462].
- 2013, qu'il soit écrit en base 2 (111110111012), en base 3 (22021203) ou en base 5 (310235), a la somme de ses chiffre égale à 9 [A135121].
- 2013 = 29²+23²-13²-5²-2². Écrit ainsi sous forme d'une somme de carrés de nombres premiers, 2013 est le premier des entiers à utiliser le nombre 29 [A089295].
- 2013 est le 11e terme d'une suite de Fibonacci commençant par 1 et 22 [A022392]
- 2013 apparaît dans le développement en fraction continue de ζ(3) [A033167].
Mais surtout, 2013 est un nombre de la forme 1 + (144 + (50 + (35 + (10 + n)*n)*n)*n)*n/120... Euh... Qu'est ce que cette propriété fait dans l'OEIS ?! [A145127]
Et au niveau des curiosités qui ne sont pas dans l'OEIS, citons que
- 2013 possède 4 chiffres différents. Ce n'était pas arrivé depuis 1987. Par contre, la prochaine date possédant 8 chiffres différents sera le 17/06/2345, la dernière étant le 25/06/1987.
- ((10/9!)*8!)*7! - 6!*5!/4! + 3!*2! + 1! = 2013
Bref : bonne année 2013 !
Et la santé !
Sources :
Fascinating Smith numbers
/http%3A%2F%2Fstorage.canalblog.com%2F54%2F29%2F210892%2F128353700_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F97%2F87%2F210892%2F113994993_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F42%2F13%2F210892%2F108236323_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F72%2F15%2F210892%2F107004083_o.png)