2013+1 (Cette nouvelle année est-elle intéressante ? Episode 05)
Nous venons de changer d'année, et, comme en chaque nouvelle année, je ne peux pas résister à l'envie de passer en revue les différentes propriétés (in)intéressantes du nombre de l'année.
Pour savoir si un nombre est intéressant, l'instrument de mesure officiel est l'OEIS, l'encyclopédie en ligne des suites entières. Plus un nombre apparaît sur l'OEIS, plus il est intéressant. A titre d'exemple, 2011 possédait 378 propriétés et était, ce ce fait, un nombre particulièrement intéressant (il faut dire que c'était un nombre premier, une vertu qui se fait de plus en plus rare chez les nombres). Les années 2012 et 2013 possèdent respectivement 121 propriétés et 96 propriétés, ce qui font d'elles des années bien moins intéressantes.
Et 2014, dans tout ça ? Eh bien... Comment dire ?... Il va falloir faire avec... C'est la crise pour tout le monde, hein ?...
2014 possède seulement 76 propriétés !
Ce n'est pas encore cette année que la courbe des propriétés va s'inverser. Mais j'ai cru comprendre que le changement, c'est l'année prochaine. Voyons tout de même ce que le nombre 2014 a à nous offrir.
Excursions de Motzkin [A057585]
Le n-ième nombre de Motzkin (noté Mn), c'est le nombre de façons de placer des cordes non concourantes sur un cercle, entre n points [A001006].
Par exemple, M4 = 9 : il y a 9 façons de dessiner des cordes qui ne se croisent pas entre 4 points d'un cercle :

En cherchant à la main, on peut voir que M1 = 1, M2 = 2, M3 = 4 et que M4 = 9.
Pour calculer les nombre suivants, il faut réfléchir de manière un peu plus récursive. Supposons que l'on vient de calculer Mn, et cherchons Mn+1. Combien y a-t-il de façons de placer des cordes entre ces n+1 points ?
Déjà, il y en a au moins Mn (il suffit d'ignorer ce n+1-ième point que l'on vient d'ajouter.
Maintenant, prenons en compte ce nouveau point, et reliant-le à l'un des autres points, disons qu'il s'agit du k-ième (n choix possibles). Cette corde sépare le cercle en deux morceaux, l'un comptant k-1 points (donc Mk-1 façons d'y placer des cordes), l'autre en comptant en comptant n-k (et donc, Mn-k placements de cordes possibles). Cette séparation offre donc Mk-1×Mn-k façons de placer les cordes.

La corde [n+1;k] sépare le cercle en deux zones, l'une comptant k-1 points, l'autre n-k.
Il y a donc Mk-1×Mn-k placements comptant cette corde.
Si on fait le compte, il y a Mn placements qui ne prennent pas en compte le n+1 points, et, pour chaque point k entre le 1er et le n-ième, il y a Mk-1×Mn-k placements comprenant la corde [n+1 ; k]. Donc :
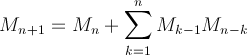
A l'aide de cette formule, on peut calculer que M5 = 21, M6 = 51, M7 = 127, M8 = 323, M9 = 835 et que M10 = 2188. Non, 2014 n'est pas un nombre de Motzkin (mais on y arrive...)
Mais il existe d'autres façons d'intérpréter les nombres de Motzkin, en particulier, celle des chemins de Motzkin : un chemin qui peut monter, descendre ou aller tout droit, et qui revient à sa hauteur de départ. Le nombre de chemins de Motzkin de longueur n est donné par Mn. Ainsi, il existe 9 chemins de Motzkin de longueur 4 :
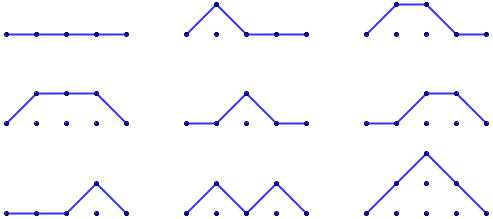
9 chemins de Motzkin de longueur 4, autant que de cercles de Motzkin.
On peut obtenir un chemin de Motzkin à partir d'un cercle cordé en le parcourant dans l'ordre de ses points. Un début de corde se traduira par un chemin montant, une fin de corde se traduit par un chemin descendant.

Exemple de placements de corde sur un cercle à 8 points, et son chemin de Motzkin de longueur 8 correspondant.
La question primordiale qui se pose alors : quid de l'aire sous les chemins de Motzkin ? Pour n=4, on peut compter que A4 = 16. Mais pour n plus grand ? On peut montrer (la démonstration en question a été coupée au montage de cet article) que l'aire totale An sous les chemins de longueur n est donnée par la formule :
On peut calculer que A5 = 56, A6 = 190, A7 = 624 et A8 = 2014.
Bref : l'aire totale sous les 323 chemins de Motkin est 2014 ! (Tout ça pour ça...) Et c'est a peu près la seule propriété qui vaut la peine d'être développée parmi tout ce que l'OEIS a à nous proposer.
Mais 2014 a de nombreuses autres propriétés intéressantes :
- 2014 correspond à la somme de 12 nombres triangulaires (nombres de la forme T(N)=1+2+3+...+N), en commençant par le 12e : 2014 = T(12) + T(13) + ... + T(23). [A119034]
- 2014 est de la forme n(n+15) : 2014 = 38×(38+15). [A132760]
- Ma préférée : 2014 = 133 - 132 - 131 - 130.[A083074]
- 5 × 22014-1 est un nombre premier. [A001770]
- 2014 peut-être écrit comme la somme de plusieurs carrés impairs distincts de 89 façons différentes, c'est plus que pour n'importe quel nombre plus petit. [A167702]
- Il y a 2014 4-uplets (a,b,c,d), où 1 ≤ a,b,c,d ≤ 7, tels que ab+cd ≤ 49. [A212150]
- Le 2014e nombre dodécahédral peut s'écrire comme la somme de deux nombres dodécahédraux. C'est plutôt rare ! [A053017]
- Le numérateur du 4028e (=2*2014) nombre de Bernoulli est divisible par 233. J'ai du mal à comprendre pourquoi cette liste existe... [A092228]
- Et c'est à peu près tout...
Du côté des propriétés qui trainent sur Twitter aux alentours du premier janvier, on a :
- 1024 + 512 + 256 + 128 + 64 + 16 + 8 + 4 + 2 = 2014 (@mikko)
- (10 + 9 ) × ((8×7) + 6 - 5 - 4) × (3 - 2 + 1 + 0) = 2014 (@alexbello)
Bref : bonne année 2014 !
Et la santé !


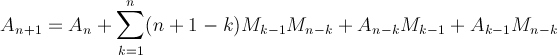

/http%3A%2F%2Fstorage.canalblog.com%2F54%2F29%2F210892%2F128353700_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F97%2F87%2F210892%2F113994993_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F42%2F13%2F210892%2F108236323_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F72%2F15%2F210892%2F107004083_o.png)