2016+1 (Cette nouvelle année est-elle intéressante ? Episode 08)

1 janvier 2017

La bonne année à tous ! Je ne blogue plus grand chose ces derniers temps, mais je ne vais pas manquer ma tradition annuelle, quantifier le niveau d'intêret de l'année à venir.

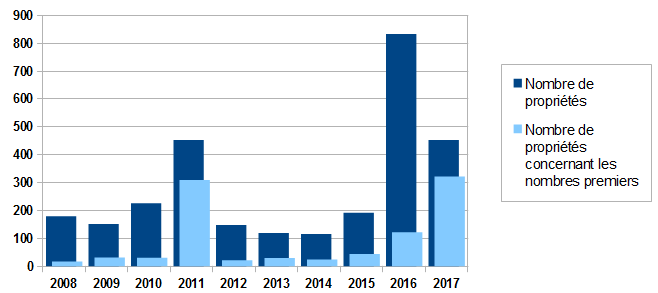
L'année 2016 a été particulièrement intéressante : découverte d'un nouveau nombre premier, de propriétés bizarres du dernier chiffre des nombres premiers ou de la surpuissance des algorithmes d'intelligence artificielle pour jouer au Go. L'année 2017 sera-t-elle à la hauteur ? Un seul outil pour le savoir, l'OEIS, l'encyclopédie en ligne des suites entières, qui répertorie les propriétés de toutes les suites intéressantes de nombres. Selon l'arithmomancie des anciens, plus un nombre est présent dans l'OEIS, plus il sera intéressant. L'année 2016 était particulièrement brillante avec pas moins de 831 propriétés répertoriées, contre 191 en 2015 ou 114 en 2014. Et pour 2017 ? Laissons parler les chiffres !

L'année 2017 possède 453 propriétés, ce qui est tout de même beaucoup
(dont 322 qui concernent les nombres premiers, ça aide pas mal)

L'année qui vient s'annonce donc particulièrement intéressante ! Mais pourquoi ? Il faut rentrer dans le détail...

A130883 : Nombre maximal de régions délimitées par 32 secteurs angulaires
Prenez un plan, et dessinez-y un secteur angulaire (deux demis-droites issues d'un même point). Il délimite alors deux régions. Dessinez-y un autre secteur angulaire. Si vous vous débrouillez bien (en évitant les parallélismes, notemment), ce sont 7 régions qui seront alors délimitées. Et pour 32 secteurs angulaires, ce ne sont pas moins que 2017 régions (au maximum) que l'on pourra obtenir.

2017___Secteurs_angulaires
1 secteur angulaire délimite 2 régions
2 secteurs angulaires délimitent (au plus) 7 régions
3 secteurs angulaires délimitent (au plus) 16 régions
32 secteurs angulaires délimitent (au plus) 2017 régions

On peut en fait démontrer que N secteurs angulaires peuvent au maximum délimiter 1 - N + 2N². Pour le voir, il faut préalablement étudier un problème qui lui est lié, le nombre L_N de régions que l'on peut obtenir au maximum en traçant N lignes droites.

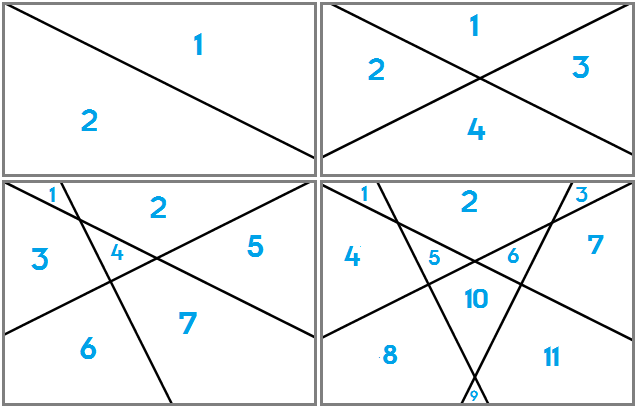
1 droite délimite 2 régions
2 droites délimitent 4 régions de plus
3 droites délimitent 7 régions de plus
4 droites délimitent 11 régions de plus

En regardant les premières valeurs, on peut conjecturer que chaque terme s'obtient à partir du précédent en ajoutant successivement 1, 2, 3, etc. En fait, quand une nouvelle droite est dessinée, celle-ci coupera chacune des droites précédentes en un unique point (pourvu que les droites ne soient pas parallèles deux à deux). Etant donné que les régions sont toujours convexes, une nouvelle droite ajoutera autant de régions qu'il y a de droites.

Bref, on a L₁ = 1 et L_N = L_N-1 + N, autrement dit L_N = 1 + 1+2+3+...+N. On reconnait dans la formule de L_N l'expression 1+2+3+...+N des nombres triangulaires, que j'avais évoqué l'année dernière (2016 étant justement un nombre triangulaire). On a donc L_N = 1 + 1/2×N×(1+N).

Revenons alors au nombre A_N de régions délimitées par N secteurs angulaires. Chaque secteur angulaire étant composé de 2 droites, on devrait retrouver dans A_N l'expression de L_2N. Un secteur angulaire seul est certes composé de deux droites, mais ne délimite que 2 régions et au non 4. On pert donc 2 régions par étapes, soit 2N régions en tout.
Finalement, A_N = L_2N - 2 N = 1 + 1/2×2N×(1+2N) - 2N = 1 - N + 2N². Ce qu'il fallait démontrer (dans les grandes lignes, je vous laisse compléter seuls les imprécisions de mon raisonnement).

A001169 : Nombre de d'octaminos verticalement convexes
On appelle polyomino un assemblage de carrés unitaires (les "cellules"). Les plus célèbres sont les polyominos à 4 cellules, connus sous le nom de "pièce de Tetris", mais on peut bien sûr en construire avec n'importe quel nombre de cellules.

En ne tenant pas compte des symétries, on compte 2 polyominos à 2 cellules ("dominos", en jaune), 6 polyominos à 3 cellules ("triominos", en bleu) et 19 à 4 cellules ("tétrominos", en rouge). On peut aussi vérifier qu'il en existe 63 à 5 cellules ("pentamino") ou 2725 à 8 celulles ("octamino")
En tenant compte des symétries, on compte 1 unique domino, 2 triominos, 5 tétrominos, 12 pentaminos et 369 octaminos.

On dit qu'un polyomino est "verticalement convexe" lorsque'on peut le découper en tranches verticales qui ne présente aucun trous. Quand on cherche à dénombrer les polyominos verticalement convexes à 8 cellules, on se rend compte qu'il y en a très précisément 2017.

Deux exemples de polyominos à 32 cellules.
Le premier est verticalement convexe, au contraire du second (les deux bandes indiquées ne sont pas convexes)

Quelques exemples d'octaminos verticalement convexes, parmi les 2017 existants.

A266532 : Nombre de tridents à la 67e étape de la construction suivante
On considère des tridents (trois segments unités issus d'un même point formant des angles de 120°), et on en place une au centre de la table. C'est l'étape 1.
Pour obtenir les étapes suivantes, on ajoute un trident à l'extrémité de chacun des tridents extérieurs disponibles de l'étape précédente.

Les étapes 1, 2, 3, 4 et 5, comptant respectivement 1, 4, 7, 16 et 19 tridents.

A la 67e étape, on obtient donc ceci, composé d'exactement 2017 tridents.

2017 sera joli ou ne sera pas

C'est mieux quand c'est animé

A180920 : Somme de cubes consécutifs égale à un carré
Fait intéressant : la somme des N premiers entiers au cube est toujours égal à un carré. Plus précisément, elle est égal au carré du N-ième nombre triangulaire, ce que l'on peut écrire de la façon suivante :

1³ + 2³ + 3³ + 4³ + 5³ + ... + N³ = (1 + 2 + 3 + 4 + 5 + ... + N)²

On peut le prouver numériquement par récurrence, mais on peut aussi s'en convaincre graphiquement par découpage, de la façon suivante.

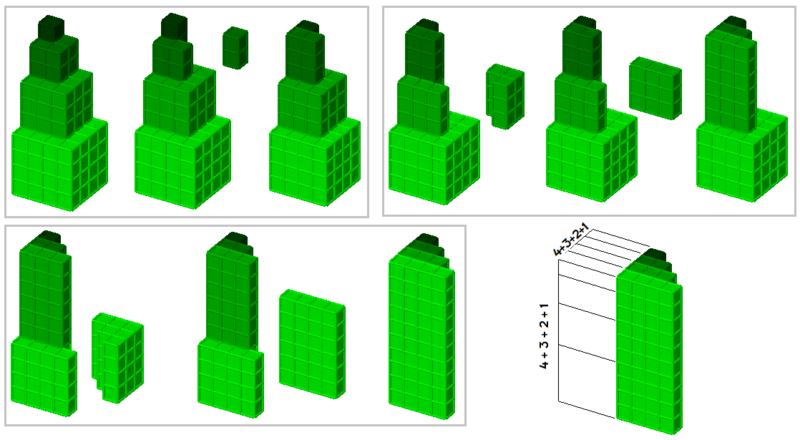
2017___Somme_des_cubes
Preuve graphique que 1³ + 2³ + 3³ + 4³ = (1 + 2 + 3 + 4)²

Bien sûr, les mathématiciens se sont demandés dans quels autres cas des sommes de cubes étaient égales à des carrés. Ils ont par exemple découvert qu'il n'y a que 5 cas où 5 cubes consécutifs forment des carrés :

0³ + 1³ + 2³ + 3³ + 4³ = 10²
1³ + 2³ + 3³ + 4³ + 5³ = 15²
25³ + 26³ + 27³ + 28³ + 29³ = 225²
96³ + 97³ + 98³ + 99³ + 100³ = 2170²
118³ + 119³ + 120³ + 121³ + 122³ = 2940²

Ils ont également découvert qu'il n'y a que 4 cas où 3 cubes consécutifs forment des carrés :

(-1)³ + 0³ + 1³ = 0²
0³ + 1³ + 2³= 3²
1³ + 2³ + 3³ = 6²
23³ + 24³ + 25³ = 204² (unique cas non trivial)

Plus tordu, existe-t-il des nombres N tels que les N cubes consécutifs en partant de N³ forment un carré ? Eh, bien, oui, il en existe une infinité, et les trois premiers sont 1, 33 et ... 2017 !

1³ = 1²
33³ + 34³ + 35³+ ... + 65³= 2079²
2017³ + 2018³ + 2019³+ ... + 4033³= 7876385²

Mais aussi...
2017 est un nombre premier ! Il faut le préciser, puisque cela amène des tonnes de propriétés liées à celle-ci :

2017 est sexy (c'est à dire qu'il fait partie d'un couple de deux nombres premiers dont la différence est 6, en l'occurence, 2011 et 2017 sont tous les deux premiers) [A023201]
2017 est le plus grand nombre premier inférieur à 47² [A053001]
2017 est un nombre premier de la forme x³ + 2y³ avec x et y positifs (en l'occurence, 2017 = 11³ + 2 × 7³) [A173587]
2017 est un nombre premier p tel que p² - p + 1 est aussi premier [A065508]
2017 est un nombre premier qui reste premier quand on ajoute le chiffre 7 entre deux de ses chiffres (en l'occurence, 2017, 27017, 20717 et 20177 sont tous premiers) [A217065]

Mais aussi...

2017 est la partie réelle du nombre quaternion (2+i+j+k)⁸ [A213421]
Il existe 2017 façons de placer les nombres 1, 2, 3, ..., 16 dans un tableau de dimension 4x4 tel que chaque ligne, colonne et diagonale soit croissante [A039917]
Il existe 2017 permutations de {1, 2, 3, ..., 7} qui ne contiennent pas le cycle (1 2 3). [A049774]

Et surtout, la santé !

Posté par El Jj à 09:58 - Commentaires […] - Permalien [#]

Tags: Nombres premiers, Suites entières, Nouvelle année, Nombres triangulaires, Polyomino, Allumettes