Deux (deux ?) minutes pour Newroz

Une nouvelle fois, j'ai adapté en vidéo un ancien article. Il est aujourd'hui question de diagramme de Venn :

Transcription :

En juillet 2012, Mamakani et Ruskey, deux mathématiciens canadiens, ont représenté Newroz, le premier diagramme de Venn symétrique simple à 11 pétales. Cette découverte vient poursuivre un idéal initié par John Venn en 1880 : comment représenter élégamment les situations de la théorie des ensembles à l’aide de patates. Ça tombe bien, j’ai deux minutes pour en parler !


L’histoire débute dans la deuxième moitié du 18e siècle, lorsque le génial Leonard Euler a tenté d’étudier systématiquement les syllogismes. Un syllogisme, c’est un raisonnement logique en trois temps, du style :
- Tous les Pokémon électrique peuvent apprendre l’attaque Tonnerre
- Or, certains Pokémon électriques sont aussi de type vol
- Donc, certains Pokémon de type vol peuvent apprendre l’attaque Tonnerre

Pour étudier ces syllogismes, Euler a eu l’idée brillante d’utiliser des cercles. Et quand bien même l’idée ne serait pas réellement de Euler, elle n’en reste pas moins brillante. Chaque cercle correspond à l’un des ensembles de l’énoncé. Dans l’exemple précédent, on a le cercle des Pokémon électriques, le cercle des Pokémon apprenant l’attaque Tonnerre, et le cercle des Pokémon de type vol. Si un élément est à l’intérieur d’un cercle, c’est qu’il appartient à l’ensemble, et réciproquement. La première hypothèse, qui énonce que tout Pokémon électrique apprend l’attaque Tonnerre, se traduit par deux cercles imbriqués. La deuxième hypothèse, qui nous dit qu’il existe des Pokémon à la fois de type électrique et vol, se traduit par deux cercles qui se coupent. On constate alors que le cercle des Pokémon de type vol et celui des Pokémon qui apprenant Tonnerre se coupent, ce qui explique la conclusion : certains Pokémon de type vol apprennent l’attaque Tonnerre.

Bref : les diagrammes d’Euler permettent de représenter des syllogismes avec trois cercles qui se coupent, ou pas.

Cent ans plus tard, le logicien John Venn met un coup de pied dans la fourmilière, et réinvente complètement l’idée d’Euler :
- la première révolution, c’est que les ensembles ne seront plus forcément représentés par des cercles, mais pourront prendre n’importe quelle forme patatoïde ;
- la deuxième révolution, c’est qu’on pourra se permettre d’utiliser plus que 3 ensembles ;
- mais surtout, la dernière révolution, c’est que tous les cas imaginables doivent être envisagés.

Avec les diagrammes de Venn, l’exemple précédent se traduira donc par trois ensembles qui s’entrecroisent en formant 8 zones distinctes, correspondant à l’intersection de 0, 1, 2 et 3 ensembles.

Pour illustrer le syllogisme par un diagramme de Venn, on va devoir griser les zones impossibles. Ainsi, puisque tout les Pokémon électriques peuvent apprendre l'attaque Tonnerre, on peut griser les deux zones correspondant aux ensembles uniquement électriques. La deuxième hypothèse nous donne l’existence d’un élément appartenant à la fois à l’ensemble vol et à l’ensemble électrique. La conclusion, c’est bien que cet élément appartient à l’ensemble Tonnerre.

Bref : les diagrammes de Venn permettent de représenter les syllogismes avec trois patates ou plus, mais qui se coupent tous les uns les autres en formant toutes les intersections possibles.
Soyons honnêtes, les diagrammes de Venn c’est sympa pour illustrer les syllogismes, mais c’est surtout très pratique pour illustrer des histoires d’intersections d’ensembles. Et du coup, il faut aller plus loin que 3 ensembles. On en veut 4, 5, 6 et plus ! Mais déjà, à partir de 4 ensembles, les problèmes commencent à arriver.

La première idée, c’est de placer ses 4 patates de façon symétrique, ce qui ressemble à ça.

Le soucis, c’est que si on compte les zones délimitées, on ne pourra en dénombrer que 14, alors que 4 ensembles donnent au maximum 16 regroupements possibles. Pour qu’un diagramme de Venn puisse être qualifié comme tel, il faut que toutes les combinaisons d’ensembles soient représentées, et il manque ici les zones correspondant à l’intersection de seulement A et B, et celle à l’intersection de seulement C et D…
Bon, en déplaçant un peu les ellipses, John Venn est parvenu à obtenir un diagramme parfait, ou chacune des 16 zones est représentée.
Pour ce qui est d’un diagramme à 5 ensembles et donc, 32 zones, Venn a proposé l’ajout d’un anneau central. Il l’a lui même reconnu, le résultat est loin d’être satisfaisant…

Solutions de diagrammes à 4 et 5 ensembles proposés par Venn

Notons tout de même une chose : un diagramme de Venn à n ensembles présente toujours 2ⁿ zones. On peut voir ça sur l’exemple du diagramme de Venn à 5 ensembles, qui contient 1 zone extérieure, 5 zones n’appartenant qu’à 1 ensemble, 10 zones appartenant à 2 ensembles, 10 appartenant à 3 ensembles, 5 appartenant à 4 et une dernière appartenant à tous les ensembles. On a bien 2⁵, c’est à dire, 32 zones.

Il existe pourtant des méthodes pour construire des diagrammes de Venn avec autant d’ensembles que l’on veut.
La première méthode est un peu braque : on part d’un diagramme à 3 ensembles, et on y trace un chemin qui entre et sort une fois de chacune des zones alors délimitée. En procédant ainsi, on délimite un nouvel ensemble, ce qui donne bien un diagramme de Venn à 4 ensemble.
On peut alors tracer un chemin qui passe par chacune des 16 zones, et on obtient un diagramme de Venn à 5 ensembles. Ce n’est d’ailleurs que depuis avril 2015 que l’on a démontré que la méthode fonctionne toujours, mais elle fournit vraiment ce qu’il y a de pire en terme de diagramme de Venn.

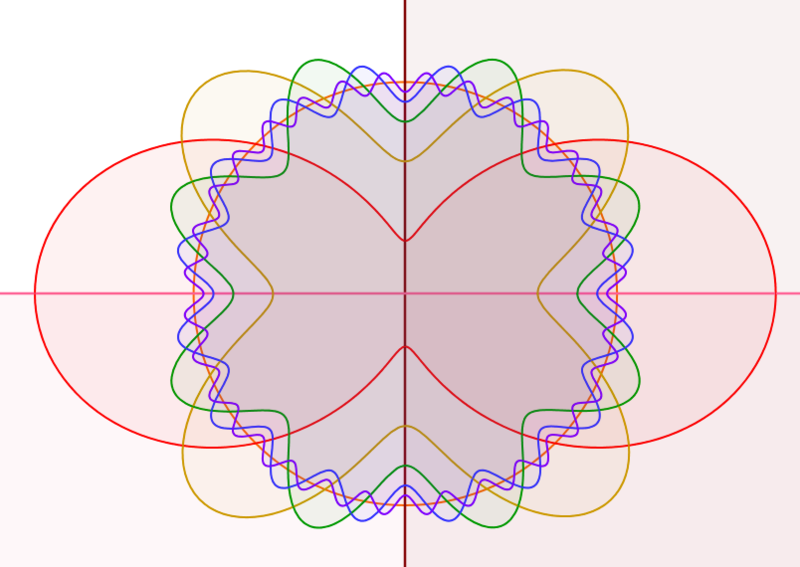
On doit sinon à Anthony Edward une autre méthode particulièrement esthétique pour construire des diagrammes de Venn, en partant de deux droites perpendiculaires et d’un cercle, ce qui forme alors un diagramme de Venn à trois ensembles. Ensuite, on fabrique chaque nouvel ensemble en faisant serpenter une courbe de part et d’autre du cercle central. Cette méthode fabriquera des diagrammes de Venn avec autant d’ensembles que l’on veut.

Solution de diagramme de Venn à n ensembles proposé par Edward

Il manque un petit quelque chose à toutes ces constructions, et ce petit quelque chose, c’est que tous les ensembles ne sont pas équivalents. Ce qu’il faudrait, c’est qu’ils soient tous identiques, mais surtout, qu’ils présentent davantage de symétrie, en se regroupant en formant une fleur. On peut fabriquer des fleurs de Venn avec 2 pétales, avec 3 ou même avec 5 : pourquoi ça ne marcherait pas avec davantage ?
On dit alors que ces diagrammes sont symétriques : chaque pétale se déduit des autres à partir d’une même rotation.
Il existe d’ailleurs des diagrammes symétriques à 7 pétales, comme par exemple celui obtenu à partir de cet ensemble là, répété 7 fois par rotation.
Ce sont ces diagrammes-là, les symétriques, qui sont à mon humble avis les plus beaux !

Et des diagrammes de Venn symétriques à 4 ou 6 pétales, alors ? On en a trouvé ? Eh bien… non ! Mais pour une raison assez simple : les diagrammes de Venn symétriques ne peuvent exister que lorsque leur nombre de pétales est un nombre premier.
Pour comprendre ça, essayons de construire un diagramme de Venn symétrique avec 4 ensembles. Un tel diagramme de Venn présente forcément 2⁴ zones. On peut même détailler : il possède 1 zone n’appartenant à aucun ensemble, 4 zones correspondant à un ensemble seul, 6 zones correspondant à l’intersection de deux ensembles, 4 zones correspondant à l'intersection de trois , et enfin, une dernière zone correspondant à l’intersection des 4 ensembles.
Le problème, c’est que dès que l’on fait un diagramme symétrique avec 4 ensembles, chaque zone apparaît soit une fois, soit 4 fois. Les zones qui apparaissent une seule fois sont la zone extérieure et la zone intérieure, tandis que toutes les autres zones apparaîtront, à cause de la symétrie, toujours par paquet de 4.
Pour les zones correspondant à l’intersection de 1 ou 3 ensembles, il n’y a pas de problème, puisqu’elles sont chacune au nombre de 4. Le soucis viendra forcément des 6 zones correspondant à l’intersection de 2 ensembles : soit il manquera deux zones, soit il y en aura 2 de trop. Le problème vient donc du fait que 6 n’est pas divisible par 4.

Ces nombres 1, 4, 6, 4 et 1 sont ce qu’on appelle des coefficients binomiaux, c’est à dire, les nombres qui apparaissent dans le triangle de Pascal, un triangle composé de nombres où chacun est égal à la somme des deux nombres juste au-dessus. En l’occurrence, 1, 4, 6, 4 et 1 apparaissent sur la 4e ligne du triangle, ce qui donne la décomposition en zones du diagramme de Venn correspondant.
Une des propriétés du triangle de Pascal, c’est que sa n-ième ligne ne contient que des multiples de n dans le seul cas où n est un nombre premier. Ainsi, puisque 5 est un nombre premier, la 5eme ligne ne contient que des multiples de 5, de même que la 7e ligne ne contient que des multiples de 7. Cette condition est nécessaire à l’existence de diagramme de Venn symétrique, ce qui explique l’existence de ces diagrammes avec 5 ou 7 ensembles.
Par contre, la 4e, la 6e ou la 8e ligne contient des nombres non multiples de 4, 6 ou 8 : il est donc parfaitement inutile d’espérer pouvoir construire de beaux diagrammes de Venn avec 4, 6 ou 8 ensembles.

Bref : si un diagramme de Venn est symétrique, il contiendra forcément un nombre premier de pétales.
Rien ne dit cependant comment on peut les construire. Ce n’est d’ailleurs qu’en 1992 que le premier diagramme symétrique à 7 pétales a été découvert, par Branko Grünbaum, qui a d’ailleurs longtemps pensé qu’ils n’existaient pas. Aujourd’hui, cependant, on en connaît beaucoup plus.

Pour 11 ensembles, ça se complique encore. Le premier exemple de diagramme de Venn symétrique à 11 pétales a été découvert en 2002 par Peter Hamburger, et il ressemble à ça !

Diagramme de Venn symétrique à 11 ensembles

Ce diagramme a un soucis majeur : il n’est pas simple. On dit qu’un diagramme est simple quand il n’existe aucun point où plus de deux courbes se croisent en même temps. Dans le diagramme de Hamburger, on trouve des points où les 11 courbes se croisent en même temps !

Existe-t-il un diagramme symétrique simple à 11 ensembles ? Eh bien, oui, mais il a fallu attendre juillet 2012 pour le voir arriver, grâce à Kaleygh Mamakani et Frank Ruskey.

Diagramme de Venn symétrique simple à 11 ensembles

Le résultat est superbe, mais il ouvre évidemment une nouvelle question : existe-t-il un diagramme de Venn symétrique et simple avec 13 ensembles ? Plusieurs mathématiciens sont à sa recherche, mais la question demeure aujourd’hui toujours ouverte !...

---

Sources :
A note on the historical development of logic diagrams : Leibniz, Euler and Venn, Margaret E. Baron
Les diagrammes de Venn, Ernest Coumet
A New Rose : The First Simple Symmetric 11-Venn Diagram, Khalegh Mamakani, Frank Ruskey,
A Survey of Venn Diagrams, Frank Ruskey, Mark Weston