Quand le 1 fait sa loi (de Benford)

Quel est le point commun entre les habitants des Pays-de-la-Loire, les chiffres de la bourse, la température de fusion des éléments et le nombre de caractères par articles dans les colonnes de Le Monde ? Vous le saurez en lisant cette note ! (Ou alors, simplement son titre...)

---

Imaginons une expérience (en fait, je l'ai vraiment faite). Prenons les 1500 villes et communes des Pays-de-la-Loire (Parce que c'est ma région, et que je l'aime bien) et notons le nombre d'habitants par communes. On se retrouve donc avec 1500 valeurs plus ou moins aléatoires. Pour chaque valeur, on va maintenant prendre le chiffre significatif (le premier chiffre à gauche. Si c'est 2545, on prend 2, si c'est 45965, on prend 4, par exemple).

Et maintenant, on va calculer la fréquence de chaque chiffre.
Puisque nos 1500 valeurs sont apparemment aléatoires, on devrait "logiquement" avoir des fréquences proches de 1/9 pour chaque chiffres :

En bleu, la fréquence du premier chiffre de 1500 valeurs réellement aléatoires (fonction rand() de gnumeric). En violet, 1/9.

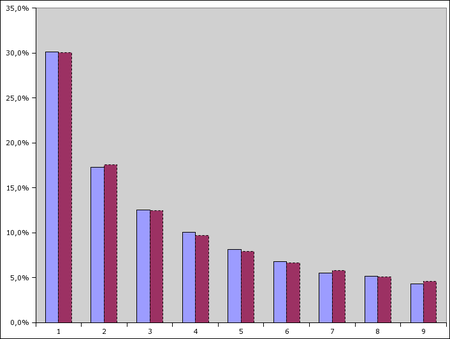
Mais ça, c'est de la théorie, puisqu'en pratique, on obtient pas du tout le graphique précédent, mais plutôt quelque chose comme ça :

En bleu, les fréquences de chaque chiffre. En violet, la fonction log₁₀(1+1/n)

Qu'est ce que l'on remarque alors ? Le chiffre 1 en première position dans près de 1 cas sur 3. Et il apparaît plus souvent que le 2, qui apparaît plus souvent que le 3, et ainsi de suite... C'est comme ça que peut se résumer la loi de Benford, ou loi des nombres anormaux...

Que ce soit pour le nombre d'habitants par ville, le rayon de covalence des atomes, la longueur des fleuves de Chine ou le prix des articles en rayon du Liddl, le 1 en première position est toujours le plus fréquent !

Et que se passe t'il quand on multiplie toutes les valeurs par 2 ? par 5 ? par 42 761 ? Quand on ajoute 15 à toutes les valeurs ? Et bien, ça reste la même chose ! Que l'on exprime en euro, en dollars ou en yen les comptes de la société Dorfneb, que l'on exprime en degrés Celcius ou degrés fahrenheit la température de fusion des divers éléments, le 1 sera toujours sur-représenté ! Et même si on exprime chaque chiffre en binaire ou en hexadécimal, on aura toujours plus de 1 (Enfin, pour le binaire, ce n'est pas étonnant, certes)!

Et vers quelle fréquence va t'on tendre, allez-vous me demander ? (Ou pas, dans la majorité des cas) Pour chaque chiffre n, la fréquence va tendre vers log₁₀(1+1/n) (les barres en violet dans le graphique un peu plus haut ; si vous changez la base dans laquelle vous exprimez vos valeur, vous changez aussi la base du logarithme)

Bon, évidemment, cette loi ne marche pas toujours. Si on prend comme valeurs la taille en mètres des habitants de Salvetat-St-Gilles, on aura bien sûr énormément de 1, mais les autres nombres ne tendront pas vers la loi de Benford.

Et à quoi donc ça sert, tout ça ? Et bien, nos amis les huissiers peuvent s'en servir pour détecter des fraudes comptables !

---

Sinon, pour l'anecdote, et pour que vous puissiez frimer dans les dîners huppés, un petit historique :
Au 19e siècle (et aussi, au 20ème), les calculettes n'existaient pas. Les logarithmes, eux, par contre, existaient, et il y avait parfois besoin de les calculer. Pour celà, on utilisait des tables de logarithmes, réunies en collections de plusieurs volumes. En 1881, Simon Newcomb, astronome américain, a remarqué quelque chose de très intéressant : le premier volume de ces tables de logarithme (avec les 1) était plus usé que les autres. Il compris que ces pages étaient plus consultées, et qu'il y avait donc plus de valeurs commençant par des uns. Il en déduisit la formule log₁₀(1+1/n), et tout le monde se moqua de lui...
En 1938, Frank Benford réalisa sa propre expérience, avec tout un tas de mesures (longueurs de fleuves, recensement) et aboutit aux mêmes conclusions que Newcomb. Il donna alors son nom à la loi découverte par Newcomb...
(Et en 1996, Terence Hill démontre la chose)

---

Sources :
* Plein d'explications compliquées
* Pour l'historique et les applications
* Et j'arrive plus à retrouver le site où j'ai trouvé les chiffres des communes des Pays-de-la-Loire, mais les graphiques sont bien de moi

Comments

[Petouche]

C'est que c'est cool pays de la loire !

[El Jj]

Pourquoi Pas > Waw, en prenant une ville totalement au hasard, je tombe sur une ville connue par une lectrice !

Whiteshoulders > Pi est plutôt un nombre conjecturé comme "normal" (Tous les chiffres apparaissent avec la même probabilité), comme e ou sqrt(2).
Par contre (après expérience personnelle), la suite de Fibonacci (http://eljjdx.canalblog.com/archives/2006/11/25/3267085.html), converge bien vers la loi de Benford, tout comme la suite des factorielles (mais là, la convergence est moins efficace)

[Whiteshoulders]

Abricto : c'est l'inventeur de la pomme golden ?

Whaou, franchement ! Mais je me pose une question tout a coup : les deciamles de Pi ou du nombre d'or suivent elles la loi de Benford ?

[Pourquoi Pas ?]

Très intéressant tout ça ;-) (juste un petit rectificatif (parce qu'il s'agit d'une ville de ma région et que je l'aime bien ^^) : on ne dit pas "Salvetat-St-Gilles" mais "LA Salvetat-St-Gilles" :D (mais c'est juste pour pinailler hein))

[Tipierre]

"Il y a certaines experiences qui ne peuvent se résumer qu'en un mot : wahou" !