¡ Ay, Carambar !
Qu'est ce qui est jaune et qui passe à travers les murs ? Une banane magique !

Le Caranougat, c'est une délicieuse confiserie au goût de nougat qui enchantera le palais des petits comme des grands ! [1]... Ne reculant devant aucun sacrifice pour faire avancer la science, j'ai accepté de corrompre l'intégrité de mon système digestif en engloutissant presque 1 kg de Caranougats, afin de répondre à la question que tout le monde se pose : combien existe-t-il de blagues Carambar ? Pour connaître la réponse sans vous farcir tout le blabla, la réponse se trouve en dessous des premières courbes.
Les blagues Carambars, inventées en 1969, c'est bien plus que de simples traits d'esprits : ce sont surtout de grands moments de franche poilade, comme le témoigne la blague suivante : "Comment appelle-t-on un chien magique ? Un magichien !".
C'est au cours de l'été que j'ai entrepris de chercher une réponse à la grande question "combien de blagues Carambars sont actuellement en circulation ?". J'ai eu de la chance, puisque les blagues du moment n'étaient ni des blagues Titeuf, ni des blagues Elie Semoun... J'ai donc déboursé de ma poche quelques euros pour acheter deux paquets de Carambars.
Malheureusement, il est pratiquement impossible de pouvoir découvrir l'ensemble des blagues. Il ya d'un côté les problèmes techniques, quand l'emballage colle au caranougat et demande au gourmand d'altérer la précieuse blague. Mais surtout, il y a beaucoup trop de blagues pour que l'on puisse toutes les découvrir en seulement deux paquets. Il faut donc procéder à des techniques statistiques avancées pour estimer le nombre de blagues.
Bon, comme je ne connais pas vraiment ces techniques de statistiques avancées, je vais me contenter de petites techniques probabilistes, avec sûrement beaucoup de défauts...
Protocole expérimental

Pour modéliser les choses, on va considérer qu'un Carambar ne possède qu'une seule blague, tirée au hasard parmi l'ensemble des n blagues existantes. En fait, un Carambar possède toujours au moins une blague lisible entièrement, mais on peut parfois arriver à 3 blagues sur un même emballage (Mais certaines blagues sont coupées avant leur chute. On ne saura jamais, je le crains, pourquoi on met une selle à un cheval ?). Chaque blague ne possédant pas toujours la même longueur, elles ne sont pas équiprobables. Pour fixer les choses, j'ai décidé que la blague d'un papier est la première blague entièrement lisible.
Après le dépouillement du premier paquet, on arrive à un total de 36 blagues différentes pour 43 Carambars dans le paquet.
Après le dépouillement du deuxième paquet et de ses 42 Carambars, on arrive à un total de 59 blagues différentes pour 85 Carambars (et de 86 blagues ou demi-blagues découvertes)
Les résultats plus précis du dépouillement sont disponibles ici.
Je tiens à préciser une horreur : il est possible que plusieurs générations différentes de blagues soient mélangées au sein d'un même paquet. En tentant de recréer la chaîne des blagues, je me suis aperçu qu'il arrive qu'une blague donnée ne suive pas forcément toujours la même blague. Il existerait plusieurs cycles de blagues... Sur les 85 Carambars, je n'en ai trouvé que 2 qui ne collaient pas avec le reste (ou inversement). Heureusement, certains enchaînements de blagues se retrouvent bien sur plusieurs Caranougats différents.
Il est à présent temps de faire parler ces chiffres !
Estimation du nombre de blagues Carambars
On cherche ici à estimer le nombre n de blagues, à partir du nombre k=85 de Carambars dépliés, et du nombre d=59 de blagues différentes recueillies. La seule information que l'on a pour l'instant, c'est qu'il y a au moins 59 blagues différentes. Si il n'y en a effectivement que 59, il est improbable que l'on réussisse à toutes les avoir en seulement 85 Carambars. Inversement, si il existe plus de 500 blagues différentes, il est improbable que l'on ait autant de doublons au sein d'un même paquet. Il faut donc réussir à mesurer ces "improbabilités", et de se dire que le nombre n que l'on cherche correspond à la situation la moins improbable...
L'idée est de chercher à évaluer la probabilité Pd,k(n) de trouver d blagues différentes en dépliant k Carambars quand il existe un total de n blagues. En évaluant cette probabilité pour chaque n, on devrait pouvoir trouver une valeur de n qui maximise cette probabilité.
On peut traduire l'énoncé en terme de mots et de lettres, en considérant qu'une blague est une lettre, et que l'ensemble des blagues constitue un alphabet de n lettres. Le dépouillement des Carambars correspond alors à un mot de k lettres, utilisant d lettres différentes. On note ad,k(n) le nombre de mots de k lettres possédant d lettres différentes dans un alphabet à n lettres. On a alors :
![]()
Malheureusement, calculer a59,85(n) n'est absolument pas évident... On peut cependant trouver ad,k(n) à partir de ad,k(d) : pour trouver toutes les combinaisons de mots de k lettres dont d distinctes parmi n lettres, on peut commencer par choisir les d lettres distinctes parmi les n lettres de l'alphabet (Cnd choix), puis chercher les ad,k(d) mots de k lettres utilisant les d lettres choisies. Par exemple, en prenant n=4, k=3 et d=2 : on commence par choisir deux lettres parmi {a,b,c,d} (disons a et b), puis on écrit toutes les combinaisons de mots de 3 lettres contenant au moins un a et un b :
aab, aba, abb, baa, bab, bba
On en déduit tous les autres mots de 3 lettres dont 2 différentes en remplaçant {a,b} par les autres combinaisons de 2 lettres possibles :
aac, aca, acc, caa, cac, cca, aad, ada, add, daa, dad, dda
bbc, bcb, bcc, cbb, cbc, ccb, bbd, bdb, bdd, dbb, dbd, ddb
ccd, cdc, cdd, cbb, dcd, ddc
Autrement dit, on a la formule :
![]()
On ne sait toujours pas calculer ad,k(d), mais on sait au moins que ce nombre est indépendant de n : on a donc Pd,k(n) proportionnel à Cnd /nk.
Le nombre n que l'on cherche doit donc se situer aux alentours du n qui maximise Cnd /nk. Les calculs pour [d,k]=[36,43] (en rouge) et [d,k]=[59,85] (en vert) donnent :


Cnd /nk en fonction de n
On remarque au passage que plus on prend de Carambars en considération, plus le pic de la courbe est fin, et donc, plus le résultat est précis. Le pic de la courbe verte se situe aux alentours de 110 (107, pour être précis).
Les calculs sont formels : il doit y avoir environ 110 blagues différentes dans les paquets de Caranougats que l'on pouvait acheter pendant les grandes vacances chez Carrefour !
Bon, la méthode employée ici n'est pas du tout la meilleure (il aurait été préférable de chercher un estimateur de maximum de vraisemblance, mais mes connaissances en statistiques étant ce qu'elles sont, je préfère laisser ça aux professionnels), et ne donne aucune idée de la précision du résultat obtenu, mais c'est quand même un bon début.
J'ai voulu améliorer la précision des calculs au cours de la semaine dernière, et j'ai donc acheté un nouveau paquet de carambars. Horreur ! Les blagues ont été remplacées par des nouvelles blagues (moins drôles) ! Qu'à cela ne tienne ! Y a-t-il plus de blagues dans la nouvelle collection ou dans l'ancienne ? Après dépouillement des 44 Carambars du paquet, j'ai trouvé 34 blagues différentes (dont une même blague en 4 exemplaires). Ce qui donne en graphique :
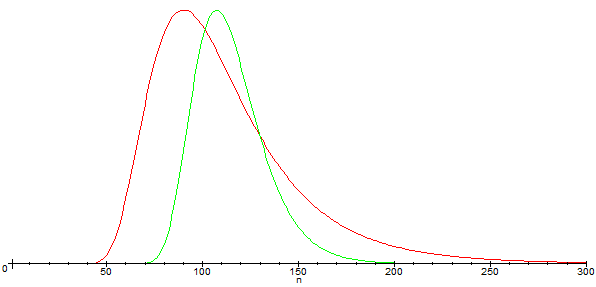
En vert, la courbe correspondant aux anciennes blagues ( [d,k]=[59,85] )
En rouge, la courbe correspondant aux nouvelles blagues ( [d,k]=[35,44] )
Non seulement, les blagues sont moins bien, mais en plus, il y en a moins !...
Faits intéressants
Pour finir, quelques statistiques intéressantes de la saison 2009-2010 des blagues Carambars :
- La plus longue blague est une blague de Toto : "Toto revient à l'école et annonce triomphalement à sa mère : « M'man, je suis le seul à pas avoir eu zéro ! La prof a annoncé les résultats du devoir de calcul : « Alain zéro, Robert zéro, Serge zéro, Toto idem. » »"
- La plus courte est une devinette : "C'est quoi un chat tout terrain ? Un cat-cat !"
- J'ai lu à peu près 8 fois la blague "Que dit une pomme de terre qui croise une chips ? Purée, t'as la frite aujourd'hui !"
- Les blagues "Quatre éléphants sont à bord d'une coccinelle. Lequel d'entre eux conduit ? Celui qui a le permis de conduire !" et "Quels animaux sont obligés de marcher pour se déplacer ? Ceux qui n'ont pas le permis" sont séparées seulement par une seule autre blague.
- Deux blagues parlent de mathématiques : "Quelle est la coupe de cheveux préférée des profs de maths ? La coupe au carré !" et "« Toto, douze bouteilles de vin à 6 euros pièce, combien ça fait ? » « A la maison, ça fait 3 jours, madame »"
- Je ne saurai jamais quelle devinette a pour réponse "un passe-porc"...
[1] Si un responsable de chez Kraft Foods passe par ici, sachez que je ne suis pas contre quelques échantillons gratuits.
Sources :
Mathématiques des papillotes, chez Je véronise. La méthode présentée ici est sa méthode, d'où viennent aussi les notations.



/https%3A%2F%2Fassets.over-blog.com%2Ft%2Fcedistic%2Fcamera.png)
/http%3A%2F%2Fstorage.canalblog.com%2F38%2F13%2F210892%2F99552251_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F21%2F69%2F210892%2F96367950_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F72%2F06%2F210892%2F94888148_o.jpg)