Fermeture ou complémentaire ?

Ce week-end, c'était les journées du patrimoine ! Et c'est bien à cause de ça que je manque de temps pour fournir un article détaillant de manière consciencieuse chaque étape de la démonstration du grand théorème de Fermat... A la place, voici plutôt un court article (écrit vite fait) sur un chouette théorème de topologie élémentaire (le genre de théorème qui n'est chouette que pour ceux qui trouvent une certaine magie à la topologie...) : le théorème fermeture/complémentaire de Kuratowski !

Dans la théorie (naïve) des ensembles, on dispose de tout un tas d'opérateurs pour s'amuser avec les ensembles : l'union, l'intersection, les complémentaires... Quand on y ajoute de la topologie, on peut parler des intervalles de ℝ (les trucs de la forme [a,b], [a,b[, au programme de la seconde la dernière fois où j'ai ouvert le programme), des ouverts, des fermés, d'adhérence, d'intérieur. Dans tous ces opérateurs, il y en a deux de particulièrement intéressants pour l'histoire qui arrive :
- Le complémentaire d'un ensemble A⊂ℝ, noté A^C (qui représente l'ensemble ℝ privé de A)
- L'adhérence (ou la fermeture) d'un ensemble A⊂ℝ, noté A^- (le plus petit fermé contenant A. Autrement dit, l'ensemble que l'on obtient en bouchant les trous de A. Par exemple, l'adhérence de [0,1[∪]1,2[, c'est [0,2]).

On remarque au passage que pour n'importe quel ensemble A, on a A^C,C=A, et A^-,-=A^-. Par contre, on peut effectuer alternativement les opérations de complémentaires et de fermeture. Essayons par exemple sur l'ensemble [0,1[ :

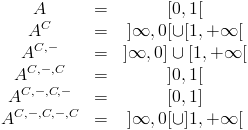
(En image)

Quand on prend la fermeture de ce dernier ensemble, on retombe sur ]-∞,0]∪[1,+∞[, que l'on a déjà vu.. Si on avait pris la fermeture plutôt que le complémentaire à la première étape, on aurait pas eu de nouvel ensemble. En prenant alternativement complémentaire et fermeture d'un ensemble, on peut donc trouver au moins 6 ensembles différents... Qui dit mieux ? C'est l'objet du théorème fermeture/complémentaire de Kuratowski : au maximum, on peut obtenir de cette façons n ensembles. Mais combien vaut n ? 6 ? 23 ? 42 ?

Avant de donner la solution, je vous laisse chercher un exemple donnant plus de 6 ensembles différents...

Kazimierz Kuratowski est un mathématicien Polonais du début du XXe siècle. Mis à part ce théorème de topologie, Kuratowski a de nombreux faits d'armes, puisqu'on lui doit une démonstration du lemme de Zorn(-Kuratowski), d'un théorème caractérisant les graphes planaires (le célèbre problème des maisons à relier en eau, gaz et électricité), et de plusieurs définitions importantes en théorie des ensembles et en topologie. C'est en son honneur, et en celui de Alfred Tarski et Wacław Sierpiński, que Bourbaki a donné aux espaces métrisables à base dénombrable le nom de "espace polonais".

Le théorème fermeture/complémentaire de Kuratowski, quant à lui, a été démontré en 1922. Il dit la chose suivante :
En appliquant successivement les opérations de complémentaires et de fermeture sur un sous-ensemble de ℝ, on peut obtenir au maximum 14 ensembles différents ! La preuve est donnée par l'exemple suivant :

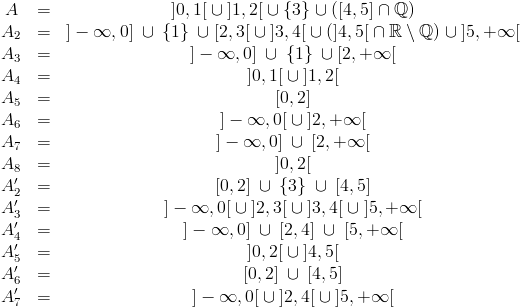
(En image)

L'ensemble ]0,1[∪]1,2[∪{3}∪([4,5]⋂ℚ) est un "14-ensemble". On prenant alternativement complémentaire et fermeture, on peut trouver 14 ensembles différents !

En fait, la clé de la démonstration du théorème vient (juste) du fait que pour n'importe quel ensemble A⊂ℝ, (ou n'importe quel espace topologique) on a A^{-,c,-,c,-,c,-}=A^-,c,-. A partir de là, on a théoriquement 14 ensembles différents :

A, A^c, A^c,-, A^c,-,c, A^c,-,c,-, A^c,-,c,-,c, A^c,-,c,-,c,-, A^{c,-,c,-,c,-,c}, A^-, A^-,c, A^-,c,-, A^-,c,-,c, A^-,c,-,c,-, A^-,c,-,c,-,c

Le fait que l'on puisse trouver un ensemble A tel que tous les ensembles ci-dessus soient différents termine la démonstration... (Et au passage, la démonstration montre que le théorème est vrai pour n'importe sous-ensemble A d'un espace topologique.)

Quand la solution d'un problème de topologie élémentaire est aussi triviale que "14", on peut en toute objectivité dire que ce théorème est beau !
La semaine prochaine, peut-être un vrai article !

---

Sources :
The Kuratowski closure-complement theorem, B. J. Gardner et M. Jackson (Pas Mickaël, Marcel...)
Variations on Kuratowski's 14-set theorem, D. Sherman, qui élargit la question aux autres opérateurs classiques de théorie des ensembles et de topologie élémentaire. 

Comments

[Fanch]

Ce n'est pas ma première étourderie ! dsl A+

[El Jj]

Robyn Slinger > Pour la topologie de Zariski, je dirais bien que des deux ensembles Ac- et A-, il y en a forcément un des deux qui est l'espace ambiant X. Je vote donc pour 6 : A, {Ac, A-, A-c} ou {Ac, Ac-, Ac-c}, X et Ø.

Fanch > Effectivement, mais si on regarde de plus près, l'ensemble [0,1]∪[1,2] et l'ensemble [0,2] représente exactement le même ensemble (Mais l'écriture est plus rapide) !

[Fanch]

"l'adhérence de [0,1[∪]1,2[, c'est [0,2]". Ce n'est pas plutôt [0,1]∪[1,2] ?
Merci bien pour ce blog que je lis depuis des semaines. Des maths pour différents niveaux. Et des maths vivantes !
A+

[Robyn Slinger]

Tiens, pour un espace topologique irréductible*, on a toujours A-c- = espace ambiant. Cela ne résout pas la question des 14 ensembles, mais à mon avis on peut obtenir une meilleure borne supérieure.

* irréductible : qui ne peut pas s'exprimer comme la réunion de deux sous-ensembles propres fermés.

[El Jj]

Je voulais que l'article soit compréhensible avec le minimum de bagage mathématiques, donc je me suis restreint à ℝ. J'ai modifié l'énoncé en conséquence.

Sur un espace topologique quelconque, le théorème dit alors que l'on peut générer au maximum 14 ensembles distincts avec les deux opérations. On pourrait s'amuser à chercher les conditions sur l'espace qui permettent à cette borne d'être atteinte...