Le labyrinthe dont vous êtes le héros
Alors que vous marchez tranquillement dans la rue, sans doute pour aller acheter le nouveau numéro de Sudoku magazine à la presse du coin, vous vous faites kidnapper par Mirator, le grand génie du mal ! Quelques heures plus tard, vous vous réveillez seul dans un lieu étrange... Vous comprenez très vite que vous êtes dans un gigantesque labyrinthe carré de dimension nxn ! Puisque Superman est en vacances et que Batman est occupé à combattre le Pingouin, vous ne pourrez compter que sur vous-même pour sortir de ce sombre labyrinthe...
Trois chemins s'offrent à vous : que faites vous ?
- Vous prenez le chemin de devant : rendez-vous page 1.
- Vous prenez le chemin de gauche : rendez-vous page 4.
- Vous prenez le chemin de droite : rendez-vous page 6.
Page 1 : Chemin de devant
Trois chemins s'offrent à vous
- Vous allez tout droit : rendez-vous page 1.
- Vous allez à gauche : rendez-vous page 4.
- Vous allez à droite : rendez-vous page 6.
Page 2 : Chemin de devant
Vous commencez à comprendre que ça ne sert à rien de prendre des chemins au hasard.
Que faites-vous ?
- Vous prenez quand même un chemin au hasard : rendez-vous page 3.
- Vous vous dites qu'il vaut mieux réfléchir, et utilisez un algorithme un peu plus intéressant : rendez-vous page 5.
Page 3 : La méthode de la souris
L'algorithme de la souris est l'algorithme le plus simple pour se sortir d'un labyrinthe : il consiste à prendre à chaque intersection un chemin au hasard, en lançant un dé, par exemple. Les théorèmes sur les marches aléatoires sont formels : en procédant de cette façon, vous avez une probabilité de 100% de sortir du labyrinthe avant la fin des temps ! Cependant, le temps que vous mettrez pour trouver la sortie sera vraiment très long (proportionnel au moins au carré de la taille du labyrinthe). L'algorithme ne nous dit pas comment revenir sur vos pas (mais le voulez-vous vraiment ?)
On peut toujours associer à un labyrinthe un graphe. D'un point de vue algorithmique, cette méthode s'apparente à une marche aléatoire sur un graphe.
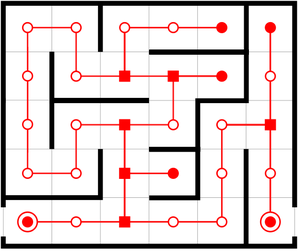
Exemple de graphe associé à un labyrinthe.
Que faites-vous ?
- Vous utilisez la méthode de la souris : rendez-vous page 15.
- Vous cherchez un autre algorithme : rendez-vous page 5.
Page 4 : Chemin de gauche
Deux chemins s'offrent à vous
- Vous allez tout droit : rendez-vous page 2.
- Vous allez à droite : rendez-vous page 6.
Page 5 : La méthode du mur
Méthode pragmatique : pour sortir du labyrinthe, il suffit simplement de suivre l'un des murs, disons le droit. Ainsi, à chaque intersection, vous tournerez à droite. En notant les endroits où l'on est passé qu'une seule fois, on peut en déduire un chemin (pas forcément le plus rapide).

L'algorithme du mur en action : le point rouge est le point de départ, le chemin en orange est le chemin obtenu en suivant le mur droit. On peut en déduire le chemin le plus rapide, en bleu.
D'un point de vue algorithmique, on a affaire à un parcours d'arbre en profondeur. Cette méthode permet de sortir à coup sûr du labyrinthe en un temps raisonnable, mais on prend le risque de visiter l'ensemble du labyrinthe.
Que faites-vous ?
- Vous utilisez l'algorithme du mur : rendez-vous page 11.
- Vous cherchez un autre algorithme : rendez-vous page 7.
Page 6 : Chemin de droite
Trois chemins s'offrent à vous
- Vous allez tout droit : rendez-vous page 1.
- Vous allez à droite : rendez-vous page 6.
Page 7 : L'algorithme de Pledge
Le principal défaut de la méthode du mur, c'est qu'il ne fonctionne pas forcément dans le cas où le labyrinthe n'est pas parfait (voir page 11). L'algorithme de Pledge (du nom de Jon Pledge) est là pour sauver la situation.
Le principe de base, c'est de longer les murs, mais en évitant de rester coincé sur un même îlot. Pour ça, il faut trouver le bon moment où se jeter dans le vide et lâcher son mur.
Dans la pratique, il faut garder un compteur dans la tête, que l'on initialise à 0 : si le compteur indique 0, on va tout droit jusqu'au mur en face. A partir de ce mur, on tourne du côté que l'on préfère (mais toujours le même, disons gauche) et on suit le mur en ajoutant 1 au compteur dès que l'on tourne à droite et en soustrayant 1 dès que l'on tourne à gauche. Si le compteur indique 0, on lâche le mur, et on va tout droit.

L'algorithme de Pledge en action : on part du point rouge (compteur en position 0) et on file tout droit. On suit alors le mur par la gauche. Dès que l'on tourne à gauche (angle bleu), on incrémente le compteur), et si on tourne à droite (angle vert foncé) on le décrémente. Si le compteur atteint à nouveau 0 (angle vert clair), on lâche le mur, et on continue tout droit.
Évidemment, cet algorithme ne marche que dans le cas où le labyrinthe est orthogonal (tous les angles sont à 90°). Cela dit, on peut adapter l'algorithme aux autres labyrinthes. Au lieu d'incrémenter le compteur de 1 dès que l'on tourne, on l'incrémente par l'angle du virage (avec son signe + ou -). Bref, cet algorithme est parfait pour se sortir d'un labyrinthe plongé dans le noir quand on atterri au milieu.
Bref, que faites-vous ?
- Vous utilisez l'algorithme de Pledge : rendez-vous page 14.
- Vous cherchez un autre algorithme : rendez-vous page 8.
Page 8 : L'algorithme de Trémaux
Il y a aussi l'algorithme de Trémaux, du nom de Charles Pierre Trémaux, à qui l'on doit cette méthode de parcours dans un graphe. D'un point de vue algorithmique, c'est encore un algorithme de recherche en profondeur (en même temps, il n'y a guère moyen de faire autrement), mais on ne peut pas rester bloqué à tourner en rond. Cette méthode demande de l'investissement : il vous faut une craie.
Lancez un dé à 6 faces :
- Si vous faites 1 ou 2, rendez-vous page 10.
- Si vous faites 3 ou 4, rendez-vous page 16.
- Si vous faites 5, 6 ou plus, rendez-vous page 13.
Page 9 : Le trésor
Vous trouvez un trésor ! Vous êtes infiniment riche !
Vous avez gagné.
Page 10 : L'algorithme de Trémaux, le retour
Il se trouve que vous avez justement une craie dans votre poche arrière gauche. Vous pouvez donc fouiller le labyrinthe avec la méthode de Trémaux !
Pour cela, marquez à la craie le chemin que vous suivez. Si vous tombez dans un cul-de-sac, faites simplement demi-tour. Si vous tombez sur une intersection que vous n'aviez encore jamais croisée, prenez le chemin que vous préférez. Si vous êtes déjà tombé sur cette intersection auparavant, faites comme si vous étiez tombé sur un cul-de-sac en faisant demi-tour, pour rejoindre la dernière intersection où vous avez fait un choix.

L'algorithme de Trémaux en action : au fur et à mesure, on peut marquer certains passages comme étant des culs-de-sac, ici en gris.
Si vous revenez à un moment où à un autre sur votre point de départ, c'est que vous avez visité la totalité du labyrinthe et qu'il n'avait aucune sortie... Par contre, si vous trouvez la sortie, rien ne vous dit que c'était le chemin le plus court !
Que faites-vous ?
- Vous utilisez l'algorithme de Trémaux : rendez-vous page 12.
- Vous abandonnez tout espoir, et, de dépit, vous creusez par terre : rendez-vous page 16.
Page 11 : La méthode du mur - suite
Malheureusement, et vous ne l'aviez pas prévu, vous n'êtes pas dans un labyrinthe parfait : les murs forment des îlots, et il n'y a pas de chemin unique pour atteindre la sortie.

L'algorithme du mur en action dans un labyrinthe non parfait : en suivant toujours le mur (gauche ou droite), on finit par tourner en rond.
En suivant la méthode du mur, vous tournez indéfiniment en rond, jusqu'à épuisement...
Rendez-vous page 13.
Page 12 : Victoire !
Très bonne idée ! Grâce à cette méthode, vous retrouvez la sortie du labyrinthe ! Vous êtes libre !
Quand on y pense, il existe une bonne douzaine d'algorithmes différents, chacun ayant sa spécificité. Certains utilisent beaucoup trop de ressources mémoires pour être utilisés par un humain. Certains sont utilisables depuis l'intérieur du labyrinthe, alors que d'autres demandent d'avoir le plan. Certains fonctionnent seulement dans le cas où l'entrée et/ou la sortie du labyrinthe sont des portes. Certains donnent le chemin le plus rapide, d'autres tous les chemins possibles...
Bref : vous avez gagné.
Page 13 : Le décès
Vous êtes mort.
Vous avez perdu.
Page 14 : L'algorithme de Pledge - suite
Ce que l'on ne vous avait pas dit, c'est que le labyrinthe n'a pas de porte de sortie ! Il y a bien une trappe de sortie, mais elle est sur un îlot, invisible à Pledge...

L'algorithme de Pledge en action sur un labyrinthe où la sortie (en jaune) se trouve sur un îlot : au bout d'un moment, on tourne en rond...
En suivant l'algorithme de Pledge, vous continuez à tourner en rond, jusqu'à épuisement... (Et, accessoirement, vous faites un dépassement de tampon sur votre compteur).
Rendez-vous page 13.
Page 15 : La méthode de la souris - suite
Vous continuez à prendre des chemins aléatoirement, jusqu'à épuisement...
Rendez-vous page 13.
Page 16 : la méthode du remplissage
Ça alors, vous trouvez par terre la carte du labyrinthe ! Et il y a un feutre juste à côté ! Ni une, ni deux, vous faites la méthode du remplissage !
Le principe est simple : il faut colorier les culs-de-sac. Si jamais ce remplissage crée un nouveau cul-de-sac, il faut à nouveau le colorier. On peut ajouter la méthode du remplissage des lacets: si jamais il existe des chemins qui rentrent et sortent de la même intersection, on peut aussi les noircir.

La méthode du remplissage en action : en orange, les culs-de-sac bouchés, et en rouge, un lacet bouché. Au final, il reste un plan relativement aisé à suivre (au pire, on applique Trémaux)
Que faites-vous ?
- Vous utilisez la méthode de remplissage : rendez-vous page 12.
- Vous vous suicidez : rendez-vous page 13.
Page 42 : sources
Labyrinth - site très complet sur les labyrinthes, avec la description de tous les types de labyrinthes, et des algorithmes pour les générer ou pour les résoudre.
L'algorithme de Pledge - chez Interstices



/http%3A%2F%2Fstorage.canalblog.com%2F72%2F92%2F210892%2F113119539_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F00%2F91%2F210892%2F107069165_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F33%2F48%2F210892%2F101190494_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F83%2F38%2F210892%2F101168363_o.png)