Évoluez-les tous !
Dans le numéro de Juillet-Août de Annals of Improbable Research (le journal des organisateurs des prix IgNobel), une équipe composée de trois entomologistes américains et du très célèbre Professeur Chen s'intéresse à l'épineux problème... de la phylogénie des Pokémon. En étudiant minutieusement leurs aptitudes, les 4 chercheurs ont réussi à recréer l'arbre évolutif des célèbres monstres de Nintendo.

Le clade des Pokémon électriques, extrait de l'arbre évolutif des Pokémon
Un arbre phylogénique est une représentation graphique des liens de parentées entres des espèces
Plus une branche est longue, plus les Pokémon sont éloignés.
On découvre sans surprise que Posipi et Négapi sont évolutivement proches, tout comme Boréas et Fulguris. La proximité entre Emolga et Electhor est un peu plus étonnante !
Phylogénie des Pokemon
L'équipe menée par le professeur Chen s'est en fait servi des méthodes de reconstruction classiques en taxinomie. Bien que celles-ci soient plus souvent utilisées pour mettre en ordre Animalia ou Platae, rien n'empêche de les employer pour ranger les Pokémon ! Dans la pratique, ils ont été définis par leur caractéristiques dans le jeu : leurs types (108 possibles), leur groupe d'œufs (16 possibles), la forme de leur corps (14 possibles) et leurs attaques (559 possibles). Une fois les données rassemblées, l'arbre final des 646 Pokémon (regroupés par familles : Pichu, Pikachu et Raichu forment un même taxon, représenté par la créature la plus évoluée) est érigé par analyse bayésienne de type MCMC.
Cette étude a mis en évidence de nombreux faits cachés par Nintendo. Par exemple :
- Le plus "évolué" des Pokémon est M.Mime ! (Se dire qu'un Pokémon mime est le summum de l'évolution est profondément désespérant)
- La vie Pokémon a commencé dans l'eau, puis est devenue terrestre de trois façons indépendantes : l'ancêtre de Locklass a donné naissance à la clade des Pokémon de glace, l'ancêtre de Marill a engendré la famille des Pokémon vol et psy (dont M.Mime) et tous les autres Pokémon dérivent d'un ancêtre proche de Kaïminus.
- Les types spéciaux (feu, plante, glace, poison, psy...) forment des clades monophylétique. Ainsi, l'ensemble des Pokémon feu descendent d'un même ancêtre aux traits canins, alors que les Pokémon plante descendent d'un ancêtre proche de Bulbizarre.
- La plupart des groupes d'oeufs forment des clades polyphylétiques : ils sont répartis à tous les coins de l'arbre. Même remarque sur la forme des corps.
Méthodes de reconstructions
Avant les années 60, la classification des espèces se basait essentiellement sur des caractères observables à l'oeil nu : morphologie, comportement... Les méthodes avaient leurs limites, un même caractère pouvant apparaître à deux endroits différent de l'arbre évolutif. C'est d'ailleurs cette classification qui a donné le regroupement des reptiles, qui n'a plus lieu d'être aujourd'hui (bien que des arguments morphologiques permettent également de réfuter l'existence d'un tel groupe). Avec l'arrivée du séquençage de l'ADN et des protéines, le domaine a évolué, donnant naissance à la phylogénie moléculaire. Pour comparer plusieurs espèces, ce sont maintenant des régions clés de l'ADN que l'on compare ; une proximité entre ces molécules implique un ancêtre commun proche (les séquences ayant muté depuis une même séquence plus ancienne).
Pour reconstituer un arbre phylogénétique, les plus simples des méthodes consistent à mesurer la proximité entre les espèces qui nous intéressent (on peut par exemple mesurer le degré de différence entre une même protéine). On consrtuit alors une matrice des distances, qui servira de base à l'élaboration de l'arbre. De nombreux algorithmes de reconstructions existent, et, grâce à la recherche, deviennent meilleurs au fil des années. Voyons dans le détail ces différentes méthodes.
L'algorithme UPGMA
Le plus simple est l'algorithme UPGMA ("Unweight Pair Group Method with Arithmetic mean") : à chaque étape, on cherche les deux OTUs ("operationnal taxonomic units", les entités que l'on cherche à classer ; ici, ce sont des Pokémon) les plus proches et on les regroupe. On transforme alors la matrice des distances M entre prenant les moyenne des deux OTUs considérées. Dans le contexte de la phylogénie, cette méthode permet de reconstruire l'arbre des espèces.
Testons plutôt sur un exemple. Nous allons prendre ce qui se fait de plus kawaï en matière de Pokémon : Rondoudou, Nanméouïe, Leveinard, Mélofée et Togepi. Les distances ont été reccueillies sur l'arbre de l'équipe de Chen. Dans la pratique, ces distances peuvent se calculer à partir du degré de ressemblance morphologique de deux espèces, ou à partir de la proximité de séquence Adn SIMILAIRES;

Les deux Pokémon les plus proches sont Mélofée et Togepi (distance de 16). Dans la matrice des distances, on remplace les valeurs par la moyenne des deux colonnes. La nouvelle matrice indique alors que les plus proches sont Nanméouïe et Leveinard (distance 19) :
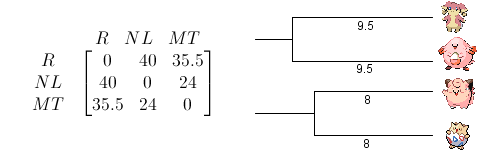
Troisième étape : on raccroche {Nanméouïe, Leveinard} avec {Mélofée, Togepi} (distance 24), puis on raccroche le tout avec Rondoudou (distance 38)
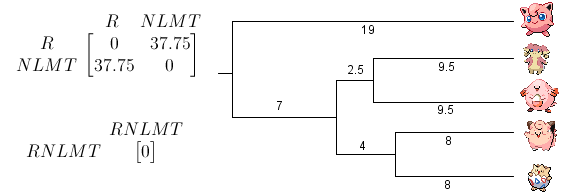
Cette méthode présente un inconvénient majeur, chaque OTU est à la même distance de la racine de l'arbre. Puisqu'il n'y a aucune raison pour que les branches aient exactement le même taux de mutation, il faut améliorer cet algorithme.
L'algorithme NJ
L'algorithme NJ (Neighbor-Joining) améliore ce point : il permet des branches de différentes tailles. Cependant, le résultat est un arbre sans racine. Pour mettre en place l'algorithme, on part d'un graphe étoilé comme celui-ci.

Le principe de NJ reste grosso le même que UPGMA, mais on change un peu la métrique pour prendre en compte l'ensemble des OTU. Pour cela, on construit une nouvelle matrice de distances Q de la façon suivante:
Q(i,j)=d(i,j)-[r(i)+r(j)]/(N-2)
où N est le nombre d'OTU, d(i,j) est la distance entre i et j, et r(i)=∑d(i,k). En fait, Q(i,j) représente l'éloignement moyen du couple (i,j) des autres OTU.
Les deux OTU les plus proches (disons i et j) selon cette nouvelle matrice sont liés par un nouveau noeud. Pour tenir compte des éventuelles longueurs de branches différentes, la distance entre ce noeud n et l'extrémité i est donné par :
d(n,i)=d(i,j)/2+[r(i)-r(j)]/2(N-2)
Reprenons l'exemple précédent. La matrice des distances M donne une nouvelle matrice Q. Celle-ci montre que Nanméouïe et Leveinard sont les plus proche. Selon la formule, le noeud intermédiaire sera placé à une distance de 7.5 de Leveinard :
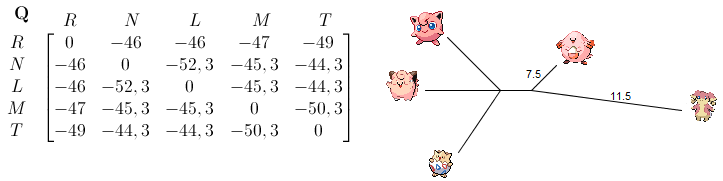
On recommence alors avec une nouvelle matrice de distances M. Dans celle-ci, i et j sont remplacées par le nouveu noeud n, sa distance avec un autre noeud k étant:
d(k,n)=(d(k,i)+d(k,j)-d(i,j))/2

Nouvelle matrice de distance
On continue alors l'algorithme avec la nouvelle matrice, ce qui donne l'arbre final :
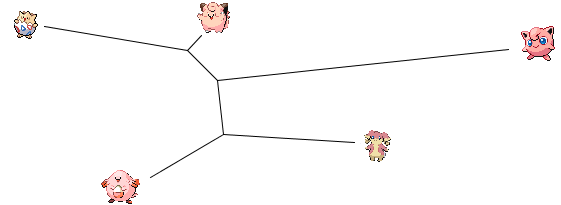
Toutes les boules roses ne se valent pas.
Et ce ne sont là que les deux principales manières d'interpréter graphiquement un tableau de distance. Mais dans la pratique, le domaine de la phylogénie n'utilise ces méthodes basées sur les distances qu'en première approche. Bien qu'elles soient rapides à utiliser, la construction des matrices de distance entraînent une grande perte d'informations.
Les méthodes de MP
Du coup, pour ne pas perdre de vue les séquences ADN, il faut les garder dans le calcul. Les méthodes les plus simples restent les méthodes MP (Maximum de Parcimonie), qui cherchent parmi tous les arbres celui qui implique le minimum de changements. Les résultats sont bien meilleurs que les méthodes basées sur le calcul des distances, mais sont bien plus coûteuses en temps de calcul.
L'idée principale de MP est de construire toutes les topologies d'arbres possibles et, pour chacun de ces arbres, calculer le nombre de mutations qu'il implique (oublions ici que les séquences d'ADN peuvent muter autrement que par substitution). On part alors de l'hypothèse que le meilleur des arbres est celui qui est le plus économe en transformations.
Le mieux, c'est de prendre un exemple. Avec quatre Pokémon (Nanméouïe, Togepi, Leveinard et Mélofée), il faut tester 3 arbres différents (avec cinq, il aurait fallu en tester 15, et la croissance est plus qu'exponentielle [OEIS : A001147]). En guise d'ADN, on va prendre la suite des 100 CT de la génération V : 1 si le Pokémon peut apprendre la CT, 0 sinon.
N : 0011010001101111111111011011110110100100010110011000000110100000001001001000100000101110010110000000
T : 0010010001100001111111000010110110100100010110011000000100100000000001001000100000101110010001000000
L : 0001011001101111110111011110111100101110010110011000000110100000001101001000110100101110010011000000
M : 0011010001101101111111011011111110100100010110011000000110100000001001001000100000101110010001000000
ADN de Nanméouïe, Togepi, Leveinard et Mélofée
Par soucis de visibilité, on va éliminer les sites n'apportant pas d'informations. En effet, si le caractère est partagé (ou non partagé) par les quatre espèce étudiées, pas la peine de s'y intéresser. On ne garde donc que 23 CT intéressantes :
N : 11011111101010011000110
T : 10000010000010000000001
L : 01111101110101111111011
M : 11011011101110011000001
ADN épuré de Nanméouïe, Togepi, Leveinard et Mélofée
Maintenant, il est temps d'évaluer le poids d'un arbre donné. Prenons celui qui relie Nanméouïe-Togepi à Leveinard-Mélofée :
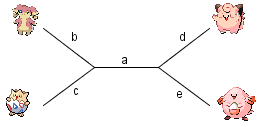
Il faut maintenant recréer le code génétique des deux ancêtres communs. Pour cela, on procède caractère par caractère.
- Le 1er caractère (CT3) par exemple, est partagé entre Nanméouie, Togepi et Mélofée : on compte donc une mutation, sur la branche e. (on pourrait aussi supposer trois mutations indépendantes sur les branches b, c et d, mais cette hypothèse est moinsprobable).
- Le 6ème caractère (CT15) est partagé entre Nanméouïe et Leveinard : deux mutations ont eu lieu indépendemment sur les branches b et e.
- Le 12e caractère (CT31) est partagé entre Mélofée et Leveinard : une seule mutation s'est produite, sur la branche a.
Au total, cet arbre implique 26 mutations.
Pour déterminer ce nombre de mutation, on peut en fait restreindre davantage le nombre de CT à analyser. Un caractère partagé entre 3 Pokémon sur 4 impliquera une seule mutation, quel que soit l'arbre. On peut donc finalement se limiter à l'étude de 4 CT :
N : 1 1 0 1
T : 0 0 0 0
L : 1 0 1 1
M : 0 1 1 0
ADN très épuré de Nanméouïe, Togepi, Leveinard et Mélofée
En faisant les compte, on peut conclure que l'arbre le plus parcimonieux est celui mettant d'un côté le couple Nanméouïe-Leveinard et de l'autre le couple Togepi-Mélofée. Tout concorde ! Tout comme la méthode NJ, l'algorithme ne permet malheureusement pas de d'obtenir un arbre.

Trois arbres possibles, un seul vainqueur.
L'approche Bayésienne
Bien que de nombreux algorithmes basés sur le principe de parcimonie existent, les reconstructions phylogéniques se servent surtout de méthodes empruntées aux statistiques et aux probabilités, à base d'inférence bayésienne (estimation de la vraisemblance d'un résultat par des arguments probabilistes). L'idée d'utiliser en phylogénie les probabilités pour estimer la vraisemblance d'un résultat n'est pas nouvelle, mais l'approche bayésienne mise au point à la fin des années 90 est aujourd'hui incontournables. C'est d'ailleurs celles-ci qui ont été utilisées par les 4 chercheurs dans leur étude des Pokémon.
L'idée générale est d'estimer, grâce à la formule de Bayes, les probabilités que chaque arbre correspondent aux données. Le problème, c'est que le nombre trop important d'arbre rend impossible ce calcul. Pour cela, on utilise une marche aléatoire (MCMC : Markov Chain Monte-Carlo) : on se promène sur l'ensemble des arbres de manière à visiter le plus souvent les arbres les plus probables. Après un très grand nombre de pas, il suffit de regarder par où l'on est passé : les arbres les plus visités seront les meilleurs.
 La clade des pokémon trop mignons, autre extrait de l'arbre évolutif des Pokémon. Celui-ci est construit par inférence bayésienne.
La clade des pokémon trop mignons, autre extrait de l'arbre évolutif des Pokémon. Celui-ci est construit par inférence bayésienne.
L'analyse phylogénétique est un domaine qui continue de progresser. Outre ses applications de généalogie d'espèces, ces méthodes peuvent aussi être employées en médecine, pour retracer l'histoire d'une contamination par un virus. Les algorithmes bayésiens n'ont d'ailleurs pas encore révélés tous leur secrets, plusieurs problèmes dans ce domaine sont encore ouverts...
Sources
Annals of Improbable Research, juillet-août 2012, volume 18, n°4
Les méthodes probabilistes en phylogénie moléculaire, Frédéric Delsuc et Emmanuel J. P. Douzery.
Génétique, phylogénie et évolution, cours du réseau Génet.



/http%3A%2F%2Fstorage.canalblog.com%2F72%2F92%2F210892%2F113119539_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F00%2F91%2F210892%2F107069165_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F33%2F48%2F210892%2F101190494_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F83%2F38%2F210892%2F101168363_o.png)