Une découpe presque parfaite
Le 15 juin dernier, lors de la soirée Radio-Dessinée “Une expérience presque parfaite” organisée par Podcast Science, Robin Jamet a proposé aux auditolectospectateurs une variante du problème du partage équitable de gâteau (que j'avais expliqué dans cet article).
Couper un gâteau de manière équitable entre gourmands se résout facilement avec le principe du "je coupe, tu choisis" : le premier gourmand coupe le gâteau en deux, le deuxième choisit la part de son choix. Si chacun cherche à maximiser la taille de sa part, celui qui coupe a tout intérêt à faire une découpe équitable.
Mais que se passe-t-il si, au lieu de faire deux parts, celui qui coupe (appelons-le A), décide d'en faire davantage ? Celui qui ne coupe pas (appelons-le B) choisit la part de son choix, puis chacun à leur tour, ils choisissent une part autour de l'ouverture jusqu'à ce qu'il n'y ait plus de gâteau. Existe-t-il une découpe qui permettrait à A d'obtenir à coup sûr plus de gâteau que B ? La question mérite d'être posée !
Ce problème a seulement été étudié par des lycéens dans le cadre de MATh.en.JEANS, donc le sujet reste encore largement ouvert.
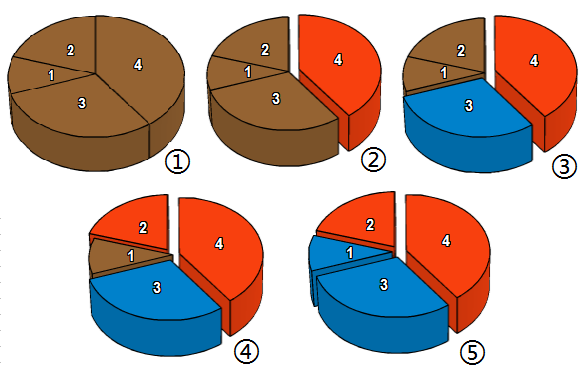Fig 1: A découpe le gâteau en quatre parts, de tailles respectives 1, 2, 3 et 4.
Fig 2 : B choisit la part de son choix, il prend la part de taille 4
Fig 3 : A a le choix entre les parts 2 et 3, il choisit la part 3
Fig 4 : B a le choix entre la part 1 et 2, il choisit la part 2
Fig 5 : A choisit la dernière part. Au final, A n'obtient que 40 % du gâteau, son découpage n'était donc pas idéal !
N=3 parts
Premier cas de figure : existe-il un découpage en trois parts qui serait profitable à A ? Malheureusement, non !
Appelons P1, P2 et P3 les différentes parts, en admettant que P3 est la plus petite et P1 la plus grande. Dans ce cas, B commencera par prendre P1, puis A prendra P2, puis A prendra P3. La part P2 étant la part intermédiaire, elle ne peut pas être plus grande qu'un demi-gâteau. Avec les parts P3+P1, B obtient donc au moins la moitié du gâteau.
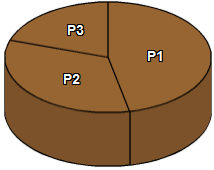Au mieux (si B cherche à maximiser sa proportion de gâteau), A ne s'en sortira qu'avec la deuxième part P2.
N=2n parts
Autre cas de figure : A propose une découpe comprenant un nombre pair de parts. Dans ce cas, B dispose d'une stratégie lui permettant à coup sûr d'obtenir plus de gâteau que A.
Numérotons les parts du gâteau. Il y a alors deux types de parts : les parts de rang pair et les parts de rang impair. L'une de ces deux familles représente au moins la moitié du gâteau ; c'est cette famille que B choisira. Disons qu'il s'agit de la famille paire.
La stratégie de B est alors la suivante : B choisit n'importe quelle part de rang pair. Quel que soit le choix de A (une part impaire), B pourra toujours choisir une part paire, et ainsi de suite.
Cette stratégie assure à B d'obtenir au moins la moitié du gâteau, mais il est possible qu'une autre stratégie lui permette d'en obtenir encore plus !
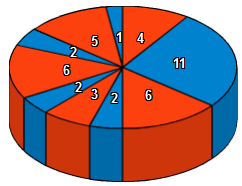
B peut s'arranger pour ne récupérer que les parts rouges (celles de rang pair), qui représentent 57% de ce gâteau.
N=5 parts
Et si A propose un découpage à 5 parts ?... Encore une fois, B disposera toujours d'une stratégie gagnante.
Appelons P1, P2, P3, P4 et P5 les différentes parts, de la plus grande à la plus petite. A l'issue du partage entre les deux joueurs, A aura deux parts, B en aura 3.
Pour qu'une stratégie gagnante existe pour A, il faut qu'au moins deux parts vérifient l'inégalité Pi+Pj > 1/2 (*) (les parts que devra choisir A pour gagner). De plus, aucune des parts ne doit être plus grande que le demi-gâteau (sinon, B la choisit en premier)
Si seuls P1 et P2 vérifient l'inégalité (*), il suffit que B choisisse en premier P1 pour empêcher A de gagner.
Il faut donc que P1, P2 et P3 vérifient deux à deux l'inégalité (*). En particulier, il faut que
P2+P3 > 1/2 (a)
Cependant, il existe pour B une stratégie obligeant A à choisir au moins l'une des parts P4 ou P5 (si P4 et P5 se touchent, B choisit en premier n'importe quelle autre part ; si P4 et P5 ne se touchent pas, B choisit en premier la part entre les deux). Il faut donc que P4 intervienne aussi dans une inégalité (*). Autrement dit, il faut (au moins) que
P1+P4 > 1/2 (b)
Les inégalités (a) et (b) sont incompatibles. En les additionnant, on trouve que P1+P2+P3+P4 > 1, ce qui est impossible. Autrement dit, il n'existe aucune stratégie gagnante pour A !
On peut montrer que la même façon qu'il n'existe pas de stratégie gagnante pour A dans le cas N=7. Pour assurer la victoire, il faut au moins que P2+P3+P4 > 1/2. En étudiant les positions relatives de P1, P2, P6 et P7, on aboutit à chaque fois à une inégalité incompatible avec la précédente.
Bref, pour que A puisse à coup sûr obtenir plus de gâteau que B, il faut un découpage comprenant au moins 9 parts...
N=15 parts
Tout espoir n'est pas perdu pour A, car il existe bien des découpages gagnants. Pour l'instant, le seul découpage découvert compte 15 parts, et ressemble à ceci :
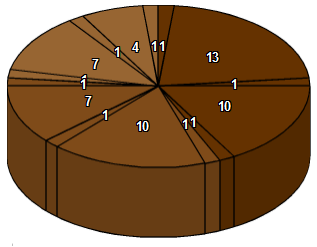Le découpage stratégique pour A :
1, 4, 1, 7, 1, 1, 7, 1, 10, 1, 1, 10, 1, 13, 1
Ce découpage de gâteau est constitué de trois portions qui suivent le même schéma : 1 - P1 - 1 - P2 - 1, où P1 et P2 sont les seules parts réellement intéressantes. Les trois portions ne sont pas équivalentes.
Pour ses deux premiers choix, A prendra ses parts parmi celles de la portion initiée par B (sauf si l'occasion est donnée par B de prendre une grosse part d'une autre partie). Pour son premier choix, A priviligiera la plus grosse part ; en cas d'égalité, il prendra la part du bord de la portion. Pour son 3e, 4e et 5e choix (la totalité de la première portion ayant été choisie), A choisira ses parts dans la plus petite des deux autres portions (les grosse parts de cette portion reviendront alors à B). Finalement, B sera contraint de laisser les deux dernières grosses parts à A. Au final, A aura (au moins) 3 parts des 6 plus grandes parts ; par cette stratégie, elles seront plus grandes que celles de B.
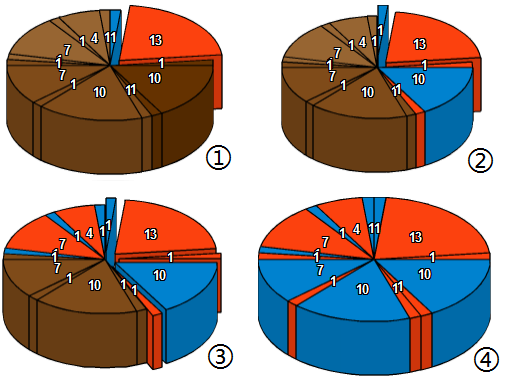
Exemple
Fig 1 : B choisit la plus grosse part "13". Parmi ses deux parts possibles, A doit choisir celle du bord de la portion.
Fig 2 : B a deux possibilités : choisir une part "1" de la petite portion (et céder les parts "4" et "7" à A), ou choisir la part "1" du milieu de la grande portion. Ce deuxième choix est plus stratégique pour B. Ensuite, A choisit la part "10", puis B choisit la dernière part de la portion.
Fig 3 : A a deux possibilités : choisir une part de la petite portion ou de la moyenne portion. En prenant celle de la petite portion, il laisse à B les grandes parts de cette petite portion, mais récupères celles de la moyenne portion (Fig 4)
Fig 4 : A récupère donc 31/60 du gâteau, contre 29/60 pour B.
Variantes
De nombreuses questions restent encore ouvertes : existe-t-il un découpage stratégique à 9 parts ? à 11 parts ? à 17 parts ? De plus, il est certain qu'il existe un bon découpage avec toutes les parts différentes (il suffit de modifier légèrement la taille des parts de l'exemple au dessus), mais existe-t-il un découpage où les 15 parts sont respectivement de taille 1, 2, ..., 15 ?
On peut aussi penser à la variante avec une barre pâtissière où A coupe la barre puis, chacun à leur tour en commençant par B, les deux gourmands choisissent l'une des parts à l'extrémité. Si le nombre de parts est pair, B dispose d'une stratégie gagnante (il peut faire en sorte que A ne récupère que les parts de rang pair ou celles de rang impair). Si le nombre de parts est impair, A dispose d'un découpage gagnant (par exemple, un découpage en 3 parts où celle du milieu est sensiblement plus grande que les deux autres).
Un partage de barre pâtissière sensiblement avantageux pour A, deuxième à choisir !
Une dernière variante, toujours avec une barre pâtissière : B choisit la part de son choix, puis, à leur tour, les gourmands prennent une part autour de l'ouverture (il peut n'y avoir qu'une seule part disponible).
Pour un nombre pair de part, B a une stratégie gagnante, toujours la même. Les cas impairs sont un peu moins évident, mais on peut montrer sans trop de difficultés que A n'a pas de stratégie gagnante pour N=1, 3, 5 ou 7 parts (en raisonnant sur des inégalités, comme pour le cas du gâteau).
Existe-t-il un découpage gagnant pour 11 parts ou plus ? La question reste ouverte ! Ami lecteur, ces questions sont pour vous !
Edit : Finalement, le problème a été étudié par une équipe de mathématiciens français et polonais en 2011 : How to Eat 4/9 of a Pizza
/http%3A%2F%2Fstorage.canalblog.com%2F38%2F13%2F210892%2F99552251_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F93%2F48%2F210892%2F89760281_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F11%2F46%2F210892%2F87126295_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F43%2F21%2F210892%2F81789135_o.png)