Quatre quatre codec !

Grenelle de l'environnement, plan Borloo, 2600€ de malus à l'achat d'un 4×4... Et si je parlais du problème d'arithmétique récréative, le problème des quatre quatres ? Et paf, dans l'actu !

Le problème basique des Quatre quatres est celui-ci : avec les 4 opérations élémentaires (celles des chiffres et des lettres, l'addition (+), la soustraction (-), la multiplication (×) et la division (/)), quatre 4 et autant de parenthèses qu'il faut, il faut écrire tous les entiers naturels (du moins, le plus possible).
A noter que ce n'est pas si évident que ça, mais voici quand même la solution.

0 = 4+4-4-4
1 = 4/4 × 4/4
2 = 4/4 + 4/4
3 = (4+4+4)/4
4 = 4 + 4×(4-4)
5 = (4×4+4)/4
6 = 4 + (4+4)/4
7 = 4 + 4 - 4/4
8 = 4 + 4 + 4-4
9 = 4 + 4 + 4/4

Niveau 0
Et pour 10 ? Et bien, avec les règles du départ, c'est tout simplement impossible ! Heureusement, on peut élargir les règles, en permettant :
- La concaténation : écrire 44 avec deux 4
- La racine carrée : √(4) = 2
- La puissance : 4⁴ = 256
- La factorielle : 4! = 24
- La virgule (enfin, le point) : .4 = 0,4 = 2/5

Et avec tout ça, on peut joyeusement continuer :
10 = 4 + √4 + √4 + √4
11 = 44/√(4×4)
12 = 4 ×(4-4/4)
13 = 4! - 44÷4
...

Et ainsi de suite... La question est entière : jusqu'où peut-on aller avec beaucoup de patience ?
Et bien, avec les règles données, il sera impossible de trouver 73.

Niveau 2
(Parce qu'il n'y a pas de niveau 1, j'ai repris la numérotation de David A. Wheeler)
Heureusement, on peut encore élargir les règles données, en ajoutant la possibilité d'écrire .4 (qui signifie 0,444..., alias 4/9).

On peut donc joyeusement continuer :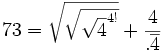

74 = (4! + 4)/.4 +4
75 = [4!/(.4+.4)]/.4
76 = 4!/.4 + 4×4

Et ainsi de suite, jusqu'à... 112.

Niveau 3 & 4
Il nous faut encore avancer... Pourquoi ne pas permettre de faire des racines n-ièmes, avec un n arbitraire ? Par exemple, on pourra écrire .
Mais en fait, même avec cette fonction, on ne peut pas écrire 113... !

On a alors besoin d'une nouvelle opération pour pouvoir avancer. La fonction qui aura la chance de nous aider à avancer sera alors... La fonction Gamma d'Euler !
Cette fonction est une généralisation de la factorielle à l'ensemble des nombres complexes, mais elle nous intéresse ici grâce à la relation Γ(n)=(n-1)!

Maintenant, on peut vraiment y aller gaiement :
113 = Γ(Γ(4)) - (4!+4)/4
114 = 44/.4 + 4
115 = (√4 + 44)/.4
116 = (4/4 + 4)!-4
etc.

Et jusqu'à où peut on aller ? La réponse, c'est 196. 197, c'est pas possible...

Niveau 5 & 6
Il nous faut encore d'autres opérateurs pour avancer ! Pourquoi pas %, le signe du pourcentage ? Ca donne une division par 100 gratuite !

C'est une bonne idée, mais ça ne servirait à rien pour obtenir 197. Il va falloir utiliser l'opérateur ². C'est vrai, c'est un peu de la triche, c'est un 2 et pas un 4, mais on a quand même l'ensemble des entiers naturels à écrire...

Et hop :
197 = [(4! + 4)² + 4]/4
198 = 44 × √4/.4
199 = Γ(4)!/(4 - .4) - Γ(√4)
200 = 4×44 + 4!

Et on continue comme ça jusqu'à... 1650... Il va encore falloir trouver de nouveaux opérateurs pour obtenir 1651...

Niveau 7 et supérieur
Et pour continuer, il va falloir utiliser des fonctions encore plus ardues, comme les opérateurs booléens ET, OU et XOU (à partir de la représentation binaires). Avec ceci, on peut atteindre 2236. Il faudra ensuite d'autres opérateurs booléens, qui permettraient d'aller jusqu'à au moins 40000.

On aurait pu parler d'autres opérateurs, comme les combinaisons, la sous-factorielle, les notations rep-digits ou la fonction partie entière.

Solution universelle
En tout cas, pour être sûr d'avoir tous les entiers, il faudrait ajouter la fonction logarithme, qui fournit la solution universelle :

---

Sources :
Le site de Gérard Villemin : toutes les solutions de 1 à 70
The Definitive Four Fours Answer Key : toutes les solutions de 0 à 40000 (à lire absolument !)
Wikipédia : parce que wikipédia, des fois, c'est bien.

Comments

[Victor]

Ah !
Une fois en cours, je m'ennuyais et avec un pote on a essayer de d'aller le plus loin possible;
Sauf que je m'étais trompé, et je lui avais posé le problème : Ecrire tout les entiers avec seulement des quatre (mais autant qu'on veut), mais une seule chaque opération. C'est beaucoup plus facile, mais on s'était quand même bien amusé.
(C'était un cours d'histoire, pour les curieux)

Sinon, plus récemment j'ai essayer à nouveau (et oui encore un cours ennuyeux, communications numériques cette fois-ci) avec cette fois la bonne règle. On est allé jusqu'à 18 avec les quatre opérations de base et la racine carrée.

[El Jj]

Tom Roud > Le principal jeu là dedans est de limiter au maximum les opérations élémentaires, et la classe des opérations utilisées, mais je doute que quelqu'un prenne la peine d'essayer d'améliorer les résultats de David A. Wheeler... !

[Whiteshoulders]

C'est vrai que le log avec les racines c'est un peu de la triche. Mais juste un peu.

Sinon, je tiens juste a dire que le jeux de mot pour le titre est excellent. Si si.

[Tom Roud]

Excellent !
Pour la fonction logarithme, c'est un peu de la triche car tu peux ajouter autant de racines carrées que tu veux, c'est équivalent à rajouter des "2" emn quelque sorte.
Y a-t-il une série où on limite aussi le nombre d'opérations (genre pas plus de N opérations élémentaires) ?

[Tipierre]

Paf dans l'actu !!!
Rien à dire d'autre...