Plenty of room at the Hilbert hotel

(J'avais déjà parlé de ces histoires d'infinis, mais ça ne fait pas de mal d'y revenir)
Pour fêter Pâques, voici une petite histoire du monde idyllique des mathématiques, qui n'a en fait rien à voir avec les cloches ou les lapins.

Dans le monde parallèle merveilleux et utopique des mathématiques, il existe un hôtel possédant une infinité de chambres. C'est hôtel, c'est l'hôtel de Hilbert.

Ce jour là, l'hôtel était complet, toutes les chambres étaient occupées, mais un nouveau client arrive. "Pas de problèmes" lui annonce le gérant de l'hôtel. Grâce au téléphone interne de l'hôtel, il téléphone simultanément à tous les clients de l'hôtel en leur demandant de passer dans la chambre d'à-coté. Le client de la chambre n se verra donc attribué la chambre n+1. Le nouveau client peut alors prendre la chambre 0, alors vide. Tous les clients ont alors leur chambre pour la nuit.

Une heure plus tard, c'est un bus qui arrive dans le parking de l'hôtel. Infini, le car, évidement, et c'est une infinité de nouveaux clients qui demandent à avoir une place dans l'hôtel. Devant cette situation, le gérant téléphone à nouveau à chaque client en leur demander de déménager dans la chambre 2n. Toutes les chambres impaires sont donc vides, et le i-ième client arrivé depuis le bus peut occuper la 2i+1eme chambre. L'hôtel est à nouveau complet, tout le monde à sa chambre.
Une heure plus tard, c'est une infinité de bus infinis qui débarquent. Après quelques minutes de réflexions, le gérant décrocha son téléphone interne pour communiquer les nouveaux ordres : le client de la chambre n doit aller dans la chambre 2n. Maintenant que les chambres impaires sont libres, le gérant explique aux nouveaux arrivant la consigne : le i-ième passager du j-ième bus s'installera dans la chambre 2ⁱ⁺¹(2j+1)-1.

Le gérant passa l'heure suivante à réfléchir à comment réagir si c'était une infinité de bus infinités qui arrivaient dans chaque étage du parking infini... Le i-ème passager du j-ième bus et du k-ième étage devrait prendre la chambre 2^{(2^i)(2j+1)}(2k+1)-1... Ca devrait marcher, se dit-il, et il retourna se coucher, il avait bien mérité sa nuit.

Mais une heure plus tard, c'est un bus d'une nouvelle espèce qui se garait dans le parking de l'hôtel : un bus infiniment tordu sur lui-même. La place avant du bus était numérotée 0, celle du fond était numérotée 1, et quand on regardait deux places du bus, on s'apercevait qu'il y en avait toujours une autre entre les deux. Chaque place était numérotée par un réel de l'intervalle [0,1], et à chaque réel de cet intervalle correspond une place du bus. Au grand malheur du gérant, le bus était plein...
"Je n'avais pas prévu ça" se dit le gérant, devant le nombre de personne qui lui fallait loger... Il pris un haut parleur, et annonça à tous les passagers qui étaient descendus du bus et qui recouvraient alors de manière continue le parking : "Je vais essayer de loger un maximum de personne, mais tout le monde ne pourra pas entrer... Vous connaissez tous bien votre numéro de siège ? Parfait, si vous êtes une fraction, vous pouvez entrer, ma secrétaire va vous donner la marche à suivre". Une infinité de passagers quittèrent la foule pour s'engouffrer dans l'hôtel, mais la marée humaine sur le parking restait dense. Le gérant repris son mégaphone pour annoncer "Si votre place est un nombre algébrique, vous pouvez entrer". Le parking restait noir de monde, malgré la file indienne infinie qui quittait la foule. "Bon, tous ceux capables de me décrire leur numéro de place peuvent entrer, les autres, je suis désolé, mais vous ne pourrez pas entrer".

Le lendemain, le gérant commença à dessiner les plans de son futur hôtel, un hôtel continu où entre deux chambre se trouve toujours une autre chambre. Le lendemain de sa construction, c'était un bus numéroté par des fonctions réels continues qui se garait dans le parking...

---

Quelques explications tout de même :

* Comment peut-on placer l'ensemble des rationnels (les fractions) de [0,1] dans l'hôtel ? L'hôtel, qu'il soit vide ou plein, peut se voir comme l'ensemble des entiers naturels 0, 1, 2, 3... (S'il est plein, on libère les chambres impaires par le procédé chambre n -> chambre 2n).
Si une place du bus est un rationnel (différent de 0 et 1), elle est de la forme p/q (avec 0<p<q). En écrivant ces nombres sous la forme d'un triangle, on peut décider que le passager n°1/2 prendra la chambre 1, le passager n°1/3 prendra la chambre 2, le passager n°2/3 prendra la chambre 3 etc.

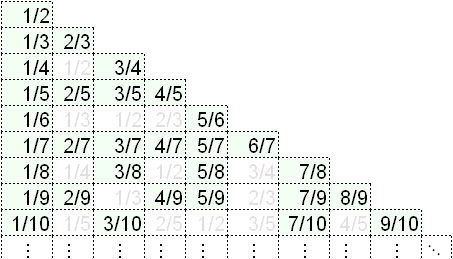
Quand on peut faire une telle correspondance entre un ensemble de nombre et , on dit que cet ensemble est dénombrable.

* L'ensemble des nombres algébrique (qui sont racine d'un polynôme à coefficients entiers), tout comme celui des nombre que l'on peut décrire est également dénombrable, mais la démonstration est moins évidente.

* Pourquoi ne peut-on pas mettre en correspondance l'intervalle [0,1] (indénombrable) avec (dénombrable) ? La façon la plus simple de le comprendre est la preuve diagonale de Cantor.
Partons du principe que chaque réel possède un développement décimal. Celui-ci est infini (même s'il n'est pas forcément unique, d'où le paradoxe 0,9999...=1, mais ça ne va pas vraiment jouer ici).
Si on pouvait mettre en correspondance cet intervalle avec , on pourrait arbitrairement décider d'un premier, d'un deuxième, etc. Imaginons que l'on peut faire cette correspondance. On peut alors mettre cette suite de réels dans un tableau, avec le développement décimal explicité :

En prenant la suite des chiffres présente sur la diagonale, on peut construire un nouveau nombre (en jaune). A partir de celui-ci, on change chaque occurrence de 0 par un 1, et tous les autres chiffres deviennent 0. Ce nouveau nombre construit est bien un réel de l'intervalle [0,1], et n'est pas présent dans le tableau (par construction). Tous les réels de [0,1] ne peuvent donc pas être organisés dans un tel tableau, puisqu'il en existe (au moins) un qui n'y est pas : C'est donc qu'on ne peut pas organiser les réels de [0,1] de cette façon ! L'ensemble des réels de [0,1] ne peut être mis en correspondance avec .

---

Sources :
Pour la science n°278 Décembre 2000, L'infini est-il paradoxal en mathématiques ?

Comments

[AlexM]

Cette notion de "nombres qu'on peut décrire" est en effet intéressante, dans l'histoire des sciences notamment. Tout ce qui pouvait être décrit ( à la règle et au compas par exemple) était dénombrable...

[El Jj]

Bertaga > C'est ce qu'explique Arthur Rainbow : un nombre est descriptible quand on peut en un temps fini en donner une propriété qui le rend unique. Un nombre indescriptible peut être par exemple celui que l'on obtient en lançant une infinité de fois un dé à 10 faces, et en notant à chaque fois le résultat... On peut le voir comme un nombre en une certaine base, donc, dénombrable. (Bon, en fait, avec le paradoxe de Richard, ce n'est pas si évident que ça de dire qu'il est dénombrable)

[Nox]

J'ai beaucoup aimé ce billet !
Je verrai bien une nouvelle, ou du moins une historiette, fantastique sur ce sujet.

J'vais garder ça dans un coin non dense et non convergent de ma chtite tête :)

[Bertaga]

C'est quoi un nombre "que l'on peut décrire" ?

[Arthur Rainbow]

Ok.

Par ailleurs, je m'en veux, j'ai mis quand même une journée avant de comprendre pourquoi la description du numéro du siège suffit:
La description utilisant les 26 lettre et un nombre fini n de caractère de ponctuation, et l'espace, la taille de la description est fini, elle est équivalent à un nombre en base 26+n+1.