Les nombres magiques

27 septembre 2008

(Pour un besoin de week-end à la mer, l'article du jour sera particulièrement court)

Le nombre 1 est déjà connu depuis vraiment trop longtemps ;
Le nombre 0 a déjà une bien longue histoire, et beaucoup de propriétés bien connues ;
On a déjà dit trop de choses sur la constante d'Archimède, plus connue par π (pi) ;
La constante de Néper e a peut-être une notoriété moindre, mais est indispensable à tous ceux qui passent leur journées à faire des théorèmes ;
Le nombre i a beau être imaginaire, sa vie sur les carnets des mathématiciens est indubitable...

Bref, tous ces nombres servent tous les jours à tous les mathématiciens du monde, tellement que Euler les a immortalisé par son identité d'Euler, qui réunit les 5 plus grandes constantes mathématiques :

Il y a aussi √2, pour son côté historique : premier nombre irrationnel qui valu la mort à celui qui l'a découvert (d'après la légende)
Il y a le nombre d'or ( (1+√5)/2 ) ou le nombre de la bête (666), pour leur propriété à faire parler bien plus d'encre qu'il n'en faudrait

Mais dans tout ça, on oublie beaucoup constantes mathématiques ; ces constantes qui ont tout de magique, mais qui ne sont la fierté que de leur inventeur...

La constante de Ramanujan : = 262537412640768744
Tapez son petit frère, , dans votre calculette : ce nombre est entier, et il vaut 199 148 648.
Mélanger un e, un π et la racine carrée d'un nombre premier, et obtenir un nombre premier ? Cela vous semble totalement impossible, et pourtant, si la calculette le dit...
Il faudrait en fait plus de décimales, pour voir que
=199148647,999978
=262537412640768743,9999999999925
Eh nan, ces nombres ne sont pas entiers ! Mais ils sont suffisamment proches pour êtres remarquables ! Beaucoup de nombre de la forme sont du même genre (avec n=6, 17, 18, 22, 25...)

La constante de Mills : A=1,30637788...
La constante de Wright : ω=1,9287800
La constante de Mills et la constante de Wright sont les objets ultimes pour fabriquer des nombres premiers aussi grands que l'on veut. En effet, pour n'importe quel entier n, les formule suivantes donne un nombre premier ! (Les crochets signifient "partie entière", les "..." indiquent la répétition de n puissances de 2)

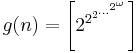
Wright

Deux formules plutôt simple, qui premettent de calculer autant de nombres premiers que l'on veut, aussi grands soient-ils !
Avec la constante de Mills, on a f(1)=2, f(2)=11, f(3)=1361, f(4)=2 521 008 887
Avec la constante de Wright, on a g(1)=3, g(2)=13, g(3)=16381
Evidement, si ça marchait, on ne se casserait pas à utiliser des milliers d'ordinateurs pour trouver les nombres premiers de Mersenne, on se contenterait d'utiliser la formule ! Alors, ou est l'arnaque ?

Pour trouver l'arnaque, on peut penser au nombre de Liouville-Erdös L. Lorsque ce nombre est placé dans la formule suivante, il retourne les nombres premiers... Dans l'ordre !

h(1)=2, h(2)=3, h(3)=5, h(4)=7, h(5)=11...
La formule est un peu plus compliquée, mais elle en vaut la peine ! Non ?...
En fait, quand on explicite L, on s'aperçoit de l'arnaque :
L=0,2003000050000007000000011000...
On obtient ce nombre en plaçant le n-ième nombre premier à la place n². La fonction h ne fait que extraire le nombre placé à la position n², ce n'est pas comme ça que l'on découvrira de nouveaux nombres premiers...
De même, dans les constantes de Mills et de Wright sont codés les nombres premiers. Mais pour calculer ces constantes, il faut préalablement connaître les nombres premiers !

Le nombre de Jj : J_j=0,7390851332...
C'est l'unique solution réelle de l'équation cos(x)=x, découvert par moi au lycée, après avoir appuyé un grand nombre de fois sur la touche "cos".
C'est un nombre qui ne sert à rien, mis à part être égal à son cosinus... Mais c'est déjà pas mal ! (En fait, on peut dire qu'il est intéressant, en ça que c'est un attracteur universel non trivial !).
En tout cas, on peut le voir dans le bandeau de ce blog depuis sa création !

En fait, il se trouve que ce nombre s'appelle également nombre de Dottie, nom donné par Kaplan en 2007... J'aurai du vieillir plus vite...

Posté par El Jj à 10:10 - Commentaires […] - Permalien [#]

Tags: Nombres premiers, Blog