Carré au scalpel

Aujourd'hui, pour célébrer la fermeture de la BU qui m'a empêché de faire un article ce week-end, voici un petit problème récréatif tout simple, qui a le seul mérite de m'avoir fait chercher trop longtemps.

Le problème est le suivant : comment découper un carré en triangles acutangles (les 3 angles de ce triangle sont aigus, strictement inférieur à 90°) qui ne se chevauchent pas ?

Le temps que vous griffonniez des carrés découpés en triangles acutangles, histoire de trouver la solution avant que je la donne, une petite interlude musicale...

=== Interlude ===

=== /Interlude ===

Avant de s'atteler à la découpe du carré, on peut se poser la question de la découpe du triangle obtus, qui donne tout de suite une solution universelle. Celle-ci, en 7 ou 8 morceaux, se révèle plutôt simple (et ingénieuse). Si le triangle ABC est obtus en B, on trace le cercle de rayon OB centré en O, où O est le centre du cercle inscrit (point de concours des bissectrices). Ce cercle coupe le triangle en 5 points, découpant le triangle obtus en 5 triangles aigus.

Découpe d'un triangle obtus en 7 triangles acutangles

Cette solution ne marche pas pour tous les triangles obtus, puisqu'il faut que les angles B-A et B-C soient inférieurs à 90°. Si l'un de ces deux angles est trop grand, il faut prendre un point D sur AC, et tracer BD. En plaçant bien le point D, on peut appliquer la construction précédente au nouveau triangle obtus BDC :

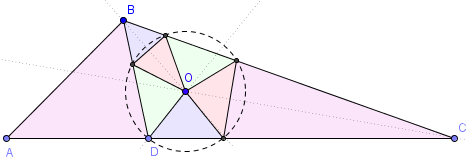
Découpe d'un triangle obtus en 8 triangles acutangles

Grâce à cette construction, on peut aboutir facilement à une découpe du carré en 10 ou 11 morceaux :

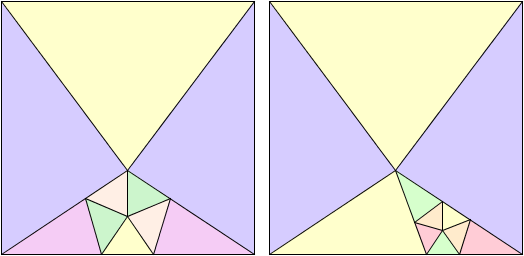
Carrés découpés en 10 et 11 triangles acutangles

Évidemment, cette astuce ne marche pas pour les solution optimales à 8 et 9 morceaux. Pour la découpe en 8 morceaux, l'astuce consiste à diviser le carré en deux rectangles égaux, puis à y tracer les deux demi-cercle d'un des rectangles. En plaçant un point à l'extérieur des demi-cercle, on retrouve facilement le découpage :

Découpe du carré en 8 triangles acutangles

A noter que la découpe en 8 triangles est minimale. Le découpage à 9 triangles est finalement le plus difficile à trouver : on y retrouve un pentagone, mais aucun triangle obtus :

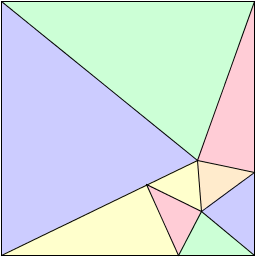
Découpe du carré en 9 triangles acutangles

Ce problème (qui ne restera pas gravé dans l'histoire des mathématiques) possède tout de même deux subtilités notables :

- Parmi les dissections présentées ici, seule la découpe en 8 triangles est une triangulation au sens topologique. En effet, c'est la seule découpe où aucun sommet ne tombe sur le côté d'un autre. La triangulation en triangles acutangles se pose alors. On connaît la solution en 8 pièces (c'est la même), on en connaît en 10 ou 11 morceaux, mais on n'en connaît aucun en 9 morceaux. En fait, on a même démontré qu'il n'en existe aucune !

- Tout problème en deux dimensions doit se poser en dimensions supérieur : comment découper un cube en polyèdres dont chacune des faces est un triangle acutangle ? La réponse, cette fois-ci, est inconnue ! Si une telle découpe existe, elle doit être d'une difficulté déconcertante ; si aucune découpe n'existe, il ne reste plus qu'à le démontrer, ce qui ne semble pas bien évident non plus.

---

Sources :
Martin Gardner - Pour la Science n°47 - septembre 1981