Becotages au pays des sphères
De quoi pourrais-je parler sur ce blog pour fêter Pâques ?... J'aurais pu parler des courbes en cloches, 11 jours après la journée de la loi de Poisson, et ainsi célébrer le mois de la probabilité, mais finalement ça sera pour l'année prochaine. Non, Pâques, c'est plutôt les œufs ! Et comme les œufs sont presque des sphères, c'est la journée idéale pour parler de sphères !
La treizième sphère
1854 : gros débat entre Gregory et Newton, à propos du grave problème du nombre d'embrassade des sphères ("kissing number").
A ma droite, Isaac Newton, physicien anglais découvreur de la gravitation universelle, et mathématicien inventeur du calcul infinitésimal (et plein d'autres trucs), soutient que l'on ne peut mettre que 12 sphères autour d'une sphère donnée.
A ma gauche, David Gregory, mathématicien et physicien écossais, inventeur (théorique) du télescope qui porte son nom, soutient que l'on peut glisser une 13e sphère !
Retour en dimension deux, pour comprendre le problème : étant donné un disque, combien peut-on placer de disques tangents au premier ne se recoupant pas. On peut expérimenter facilement la question avec des pièces de monnaies, et la réponse se trouve facilement. En effet, une fois 6 pièces posées autour de la première, on s'aperçoit que chaque pièce est tangente à ses voisines, ce qui ne laisse aucune place libre pour une septième pièce. On remarque que les centres se placent sur un hexagone régulier.

6 cercles embrassant, placés aux sommets d'un hexagone
L'objet de la querelle se passe en dimension 3. C'est maintenant aux balles de ping-pong que l'on s'intéresse : combien de balle peut-on placer autour d'une balle donnée. On peut procéder de la même façon que pour le cas à deux dimensions : par l'expérimentation !
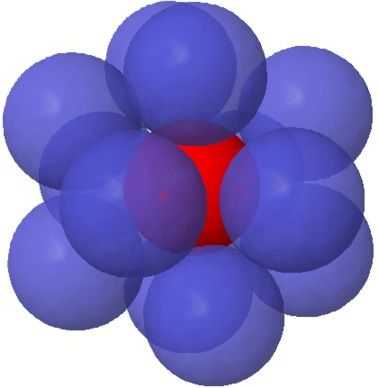
12 sphères, placés sur les sommets d'un icosaèdre
On peut facilement placer 12 boules autour de la boule centrale, mais, contrairement au problème à 2 dimensions, les boules ne sont pas tangentes les unes aux autres, il reste de la place entre les boules ! Peut-être qu'avec un peu d'astuce, on pourrait réussir à placer les boules de manière à ce qu'il reste suffisamment de place pour en placer une treizième ? C'est ce que soutient Gregory !
Il appuie sa position sur sur le fait que le rapport entre l'aire d'une calotte sphérique et celle de la sphère vaut 14,9... Explications (en deux dimensions, c'est plus simple !) :
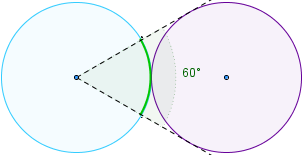
Plaçons deux cercles de même rayon côte à côte, tangents. En se plaçant au centre du premier cercle, on voit le deuxième cercle sous un angle de 60°. Si le cercle est de rayon 1, l'arc de cercle délimité par l'angle (la calotte) aura une longueur de π/3. La longueur totale du cercle étant de 2π, on peut voir que l'on peut placer au maximum 2π/(π/3))=6 cercles autour du premier. Puisqu'une configuration à 6 cercles a été trouvée, c'est que cette configuration est maximale !
Retour en 3 dimensions. Depuis le centre d'une sphère (simplifions : de rayon 1), une deuxième sphère tangente sera vue dans un cône d'angle 60°. On peut également calculer l'aire de la surface de la calotte, qui vaut ici (2-√3)π (environ 0.2679π). L'aire de la surface de la sphère est de 4π, et 4/(2-√3) ≈ 14.92. Ce calcul montre que l'on peut placer au maximum 14 surfaces d'aire (2-√3)π sur le pourtour de la sphère ; on peut potentiellement placer 14 calotte autour de la sphère, ie, 14 sphères autour de la sphère !
Cette démonstration ne permet pas de donner le nombre maximum de sphère répondant au problème, mais permet au moins d'en donner une limite supérieure. Gregory ne croit pas vraiment aux 14 sphères, mais pourquoi pas 13 sphères ?
≈≈≈≈≈≈≈
Admirez la richesse des effets spéciaux !
De l'eau a coulé sous les ponts, et c'est au XXe siècle que de nouvelles démonstrations tombent. De nombreuses incomplètes, jusqu'en 1953, où Bartel et Schütte publient la première preuve notable, donnant raison à Newton. Avec ces preuves, on est sûr d'une chose : il ne peut y avoir 14 sphères s'embrassant autour d'une autre. C'est pour éliminer la treizième sphère que les choses se corsent, mais la démonstration est bonne si on ne se plonge pas dans les détails. De nombreux auteurs ont revu la démonstration en l'améliorant, mais il n'existe aucune preuve 100% vérifiée que la conjecture de Newton est correcte (mais on en est quand même plutôt proche !)
Pourquoi avoir mis autant de temps pour résoudre ce problème ? Contrairement au problème en 1ere ou 2eme dimension, les sphères autour de la sphère centrale ne sont pas rigide, et disposent chacun d'un petit espace où glisser. On dispose donc d'une infinité de possibilité de placer les 12 sphères. On peut notamment les placer sur les sommets d'un icosaèdre (polyèdre à 20 faces triangulaires) ou d'un cuboctaèdre (polyèdre à 14 faces : 6 carrés, 8 triangles équilatéraux) :
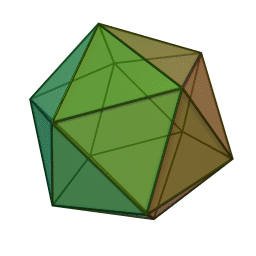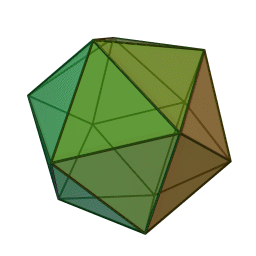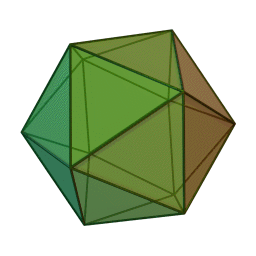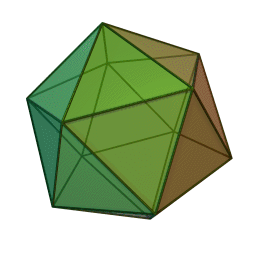

A gauche, l'icosaèdre ; à droite, le cuboctaèdre
Comme très souvent, quand les mathématiciens bloquent sur un problème, ils essaient d'en résoudre un plus difficile (ça permet souvent de statuer sur les cas particuliers). Dans ce cas là, c'est le problème équivalent dans les dimensions supérieures qui sont intéressantes. Je ne parle pas du problème en dimension 4, 5, 6 ou 7, puisque le problème est toujours ouvert (on ne dispose que d'encadrements), mais en dimension 8, les choses sont meilleures...
En effet, le problème en dimension 8 (résolu à la fin du XIXe siècle) est d'une incroyable facilité comparé à la troisième dimension : le plus grand réseau que l'on peut faire autour d'une sphère centrale est de 240 sphères ! Encore une fois, c'est la rigidité de la construction qui permet de trancher : le 8-polyèdre donnant le réseau à 240 sphères est unique, et c'est toujours plus facile de reconnaître une réponse quand elle est unique !
Pour l'anecdote, les 240 sphères sont de rayon √2, et les centres des sphères sont positionnées aux points ayant des coordonnées de la forme (0,0,0,±1,±1,0,0,0) (deux 1 en n'importe quelle position et de n'importe quel signe) et (±½,±½,±½,∓½,∓½,∓½,∓½,∓½) (un nombre impair de signes -).
Ce réseau est la base du groupe de Lie E8, un objet fondamental de la théorie des groupes en algèbre, décodé en mars 2007 ; ses applications ne sont pas encore connues, mais il est certain qu'elles auront d'énormes retombées pratiques dans le domaine de l'informatique, la physique, la chimie et de tous les domaines des mathématiques !
On connaît également la solution exacte pour la dimension 24 : c'est un réseau qui comporte 196 560 sphères !
Sources :
La treizième sphère (Marcel Berger) - Octobre décembre, Pour la science/Dossier n°41



/http%3A%2F%2Fstorage.canalblog.com%2F77%2F73%2F210892%2F111515552_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F43%2F78%2F210892%2F106322231_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F16%2F78%2F210892%2F106207701_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F63%2F97%2F210892%2F99779882_o.png)