Une orange + une orange + une orange

10h50, rayon fruits & légumes du Leclerc du coin
- Sur la liste, ya quoi ?
- Bananes, pommes et oranges. Tiens, regarde, elles sont, là peux en prendre quelques unes ?
- Hey, elles sont disposées selon un empilement hexagonal compact !
- Hein ?...
- Attends, je t'explique !
- Ho, nan...

Comment empiler des sphères de façon à ce qu'elles prennent le moins de place possible ? Kepler, bien connu des astronomes pour ses trois lois régissant le mouvement des planètes, est plutôt connu des matheux pour sa conjecture en 1611 à propos de l'empilement d'orange. En 1900, le problème était toujours pas résolu, et était suffisamment important pour faire partie des 23 problèmes de Hilbert, les grands problèmes du XXe siècle (C'est en fait la troisième partie du 18e problème). Il a fallu attendre 1998 pour que Thomas Hales donne une démonstration de la réponse, même si cette réponse était déjà connue de tous les vendeurs de fruits et légumes depuis des milliers d'années !

(Pour dire la vérité, Kepler n'a pas été le premier à énoncer cette conjecture. L'Histoire a oublié que, 11 ans plus tôt, Thomas Harriot a énoncé cette question pour déterminer la densité maximale que pourrait attendre un solide (En considérant les atomes comme des sphères))

Empiler des sphères
Revenons donc à cette question existentielle : comment empiler des oranges pour qu'elles prennent le moins de place possible ? (On parle d'un nombre infini de sphères, pour ne pas s'embêter des boîtes dans lequel on place les oranges) En fait, il suffit d'essayer d'empiler des oranges pour trouver la solution :

- Première étape : le problème en 2 dimensions. On commence par poser les oranges sur la table. Deux organisations s'offrent alors : le réseau en carrés ou le réseau en triangles équilatéraux.

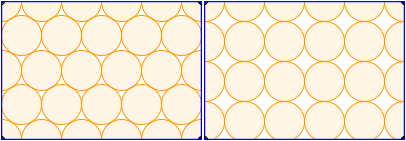
A gauche, un réseau en triangles ; à droite, un réseau en carrés

On voit tout de suite que le réseau en triangles, à gauche, minimise les trous. D'un côté, le réseau carré remplit 78% de la surface, de l'autre, le réseau triangulaire en remplit 91%. On va donc garder ce réseau comme première couche, puisqu'on cherche quelque chose de dense !

- Deuxième étape : rajouter des couches. On a en effet une première couche d'orange, il suffit de poser de nouvelles couches pour avoir un empilement. Pour l'avoir compact, il suffit de poser une orange sur l'un des trous, et de compléter. Les oranges se pose d'elles-mêmes, mais on a quand même plusieurs choix possible :

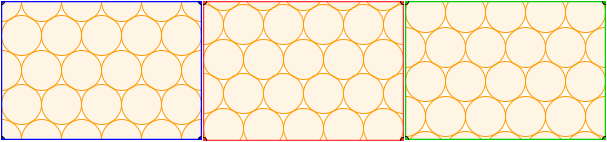
Trois types de couches : couche A, couche B et couche C

Sur la couche A, on peut poser la couche B ou la couche C (chaque orange tombe parfaitement dans l'un des trous de la première couche). On continue à ajouter des couches pour former l'empilement. La succession des couches donne différent types d'empilages :

...-A-B-A-B-... : empilement hexagonal compact
...-A-B-C-A-B-C-... : empilement cubique à faces centrées

Cela donne finalement une infinité d'empilements différents possibles ! Le bon côté, c'est que tous ces empilements ont la même densité : la proportion d'espace rempli sera de 74%.

A noter tout de même : chacune des sphères est entourée de 12 autres sphères !

Le meilleur empilement ?

Peut-on espérer obtenir un empilement de sphères encore plus dense ? Kepler conjecture que non, et l'histoire lui donnera raison, mais faut-il encore le démontrer ! L'empilement le plus dense serait le plus évident... C'est trop beau pour y croire !
En fait, pour la première couche, on a arbitrairement posé toutes les sphères sur une surface plane. Peut-être peut-on encore minimiser les espaces vides en ne prenant pas une surface de base plane ?
Autre détail : on a choisit de faire des empilement régulier... Qui a dit qu'ils devaient être réguliers ?!

En regardant de plus près les empilements que l'on a fabriqué plus haut, on s'aperçoit de la présence de tétraèdres (une pyramide à base triangulaire) et d'octaèdres (deux pyramides à bases carrés collées), en reliant les centres des sphères qui se touchent :

A gauche, un tétraèdre ; à droite, un octaèdre

Dans un tel type d'empilement, chaque tétraèdre est adjacent à 4 octaèdre, et chaque octaèdre touche 8 tétraèdres. Cela donne donc deux types de vides dans l'empilement : les vides au centre des tétraèdres et les vide au centre des octaèdres.

Vides laissés au centre des tétraèdres et des octaèdres

Proportionnellement, les vides laissés aux centres des tétraèdres sont plus petits que ceux aux centres des octaèdres. Il faut donc maximiser le nombre de tétraèdres dans notre empilement pour le densifier !
La première idée est de faire un empilement seulement à partir de tétraèdre, il suffira de placer la sphère aux sommets pour avoir un empilement parfaitement dense... manque de pot : c'est impossible ! (Il y a juste à se faire des petites pyramides en papier pour s'en convaincre).
On peut quand même essayer de faire le plus gros assemblage de tétraèdres possibles, quitte à compléter par des polyèdres pas du tout réguliers après. Comme on s'en doute, c'est voué à l'échec ! Cette méthode permet de gagner localement de la densité, mais avec au moins 53 sphères, un empilement avec des tétraèdres sera toujours moins dense qu'un arrangement tétraèdres/octaèdres des vendeurs d'orange !

Et pour démontrer ce genre de chose, il faut s'armer de courage ! Puisqu'il existe une infinité de façon de faire des empilages de sphères réguliers ou non, il est impossible de les étudier toutes individuellement. La première étape a donc été de se ramener à un nombre fini de types d'empilement. Cela a été fait : 5000 types d'empilement à examiner minutieusement ! L'ordinateur a été un allié essentiel pour Thomas Hales.

La démonstration date de 1998, mais est toujours au stade de la vérification ! Pour l'instant, elle est satisfaisante à 99% ! Hales ne se décourage cependant pas : il a lancé le Flyspeck project, projet qui consiste à réécrire sa preuve de manière formelle pour qu'un ordinateur puisse la vérifier ! (Et enfin faire accepter sa preuve par la communauté mathématique...)

Finalement, le problème de Kepler est vraiment similaire au problème de la treizième sphère : une question simple, une réponse évidente et intuitive et des complications inattendues qui ne font rien qu'à décourager les mathématiciens qui s'y collent !

---

Sources :
La conjecture de Kepler démontrée - Pour la science, N°259, mai 1999

Comments

[Victor]

Bonjour,

J'adore ce blog. Dès que j'arrive dessus et que je vois un nouvel article, avant de le lire je sais que je vais adorer.

Bravo.