Encore plus fort - Sprague & Grundy
Jeu des bâtonnets :
20 bâtonnets sur la table. Chacun votre tour, vous prendrez 1, 2 ou 3 bâtonnets de votre choix. Celui qui prendra la dernière aura la main brûlé.
Le jeu du tableau :
Un tableau de 4x4 cases devant vous, un pion par
case sur la première colonne. Chacun votre tour, vous déplacerez le
pion de votre choix d'autant de case que vous voulez vers la droite ou
vers le bas, plusieurs pions pouvant se trouver sur la même case. Celui
qui ne peut plus jouer sera fusillé sur place publique.
Jeu de Nim :
Plusieurs tas de pièces devant vous. Chacun votre tour, vous prenez autant de pièces que vous voulez dans le tas de votre choix. Celui qui ne pourra plus prendre de pièce sera goudronné et emplumé.
Jeu de Grundy :
Devant vous, plusieurs piles de pièces. Chacun votre
tour, vous choisirez une pile, et la couperez en deux piles de taille
inégale. Celui qui ne pourra plus jouer (puisque toutes les piles
seront de taille 1 ou 2) sera condamné à écouter l'ensemble du r'n'b
français.
Quart de singe :
Chacun votre tour, vous dites une lettre, de manière à former un mot. Si la lettre que vous donnez ne permet pas de former aucun mot, vous serez coulé dans le béton.
-
Tellement d'exemples qui permettent de se rendre compte d'une chose : dans la société d'aujourd'hui, connaître le théorème de Sprague-Grundy est devenu quelque chose de vital !...
Tous ces jeux ont un point commun, ils sont impartiaux. Autrement dit :
- Le jeu est commun à tous les joueurs : pas de secrets, pas de hasard, les mêmes pions pour tout le monde.
- Le but du jeu est d'empêcher l'adversaire de jouer.
- On ne peut faire durer indéfiniment une partie, ni terminer en match nul.
Sprague et Grundy (qui ont découvert le même théorème chacun de leur côté dans les années 30) nous apprennent ceci :
Il existe une stratégie qui permet à l'un des deux joueurs de gagner à coup sûr
Suivant la configuration de départ du jeu, l'un des joueur sera chanceux, l'autre non. Si le joueur chanceux effectue les bons coups, il pourra gagner à coup sûr, le joueur malchanceux sera de son côté forcé de suivre. Au moindre coup de travers, le joueur malchanceux peut reprendre le contrôle de la partie, et emmener son adversaire à la défaite.
On peut résumer en disant que le joueur qui ne connaît pas Sprague-Grundy perdra dans 99% des cas !...
Le jeu du graphe - Jeu des bâtonnets
Il existe une stratégie gagnante, c'est chouette... Mais quelle est-elle ? Pour le comprendre, jouons ensemble au jeu du graphe (à un pion). Tout d'abord, il faut dessiner un graphe, c'est à dire, un ensemble de "nœuds" (ou case) reliés les uns aux autres par des flèches, les arcs, permettant le déplacement des pions. On place un pion sur la case initiale du graphe (le nœud en losange) et le but du jeu est de l'amener sur la case double-cerclée. Un coup consiste à déplacer le pion d'une case à l'autre en suivant un arc du graphe. Prenons par exemple le graphe ci-dessous.
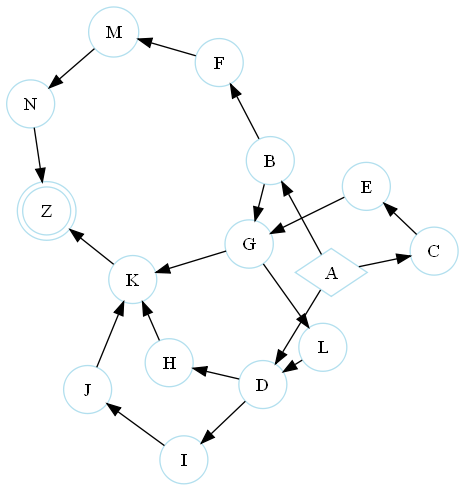
On place le pion en A, il faut l'amener en Z. Au premier coup, le joueur commençant a le choix entre B, C et D.
Grâce au théorème de Sprague-Grundy, on peut le dire : le joueur qui commence risque fort de gagner, s'il y met un peu du sien. Pour en arriver à ce résultat, il faut marquer d'un entier (appelé "nimber", excellent jeu de mot entre "Nim" et "number") chaque point du graphe en appliquant la règle du mex (minimum excluded value). Pour cela, on commence par les cases finales, qui ont un nimber de 0. Ensuite, on marque les autres cases de proche en proche, en prenant le plus petit entier non accessible depuis la case considérée. Cette définition mérite un exemple :
On commence par marquer les cases finales. Ici, on marque d'un 0 le nœud Z.
Puisque à partir de K, on peut atteindre 0 (Z), le plus petit entier non atteignable depuis K est 1. Le nimber de K est donc 1. On continue en remplissant les autres cases de proche en proche.
Le graphe entièrement rempli ressemble à ça :

Graphe des nimbers
Grâce à cette numérotation des positions, on peut depuis n'importe quelle case amener le pion sur une case de nimber inférieur. Si le pion est sur une case nulle, il sera toujours amené sur une case non nulle.
La stratégie gagnante est de s'arranger pour toujours placer le pion sur une case de nimber nul.
Ici, la position initiale n'est pas nulle (elle vaut 3). Le premier joueur a donc tout le loisir de placer le pion en B, et de se ramener à un nimber nul. Peu importe le coup de son adversaire, il continuera à placer le pion sur une case de nimber nul, jusqu'à la case Z. Victoire du premier joueur !
Le jeu des bâtonnets est exactement un jeu du graphe à un pion. 20 cases, correspondant au nombre de bâtonnets restant. La case initiale est "20", la finale est "1" et un déplacement correspond à enlever 1, 2 ou 3 bâtonnets. Les cases de nimber nul (les positions gagnantes) sont bien celles de la forme 4n+1 !

Graphe du jeu des bâtonnets et son graphe des nimbers
Le jeu du tableau
Le jeu du graphe est plutôt facile finalement : il n'y a qu'un seul pion. Mais comment faire dans un jeu comme le jeu du tableau, où il faut maîtriser 4 pions à la fois ? La solution : le jeu de Nim !
Le jeu du tableau reprend les règles de bases des jeux impartiaux : chacun son tour, on bouge un pion, le perdant est celui qui ne peut plus en bouger. On joue sur un tableau 4x4 et, depuis une case donnée, on peut bouger le pion vers la droite ou vers le bas (Le pion en A2 peut aller en A3, A4, B2, B3 ou B4). Cette fois ci, on commence avec 4 pions, tous placés sur la première colonne.

Tableau initial
Nous sommes face à un jeu impartial, il existe donc une stratégie gagnante pour l'un des joueurs. Pour découvrir laquelle, appliquons à nouveau la technique du mex. La case finale est la case D4, son nimber est donc 0. On trouve ensuite que les nimber de D3 et C4 sont 1 (Depuis D3, on ne peut aller qu'en D4. le plus petit entier non atteignable est donc 1), celui de C3 est 0, etc.
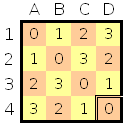
Tableau des nimbers
Cette fois ci, on ne peut plus appliquer la technique du jeu du graphe, puisqu'il y a 4 pions. Mais Sprague-Grundy ne s'arrête pas à cette première difficulté ! Il y 4 pions, certes, mais il y a surtout quatre fois 1 pion ! Au lieu de calculer le nimber d'une case, il faut calculer celui de la configuration des 4 pions. Le nimber d'une configuration se calcule facilement : c'est la nim-addition des nimbers des cases où sont les pions (Vous savez, l'addition binaire sans la retenue !)
La stratégie gagnante reste toujours la même : il faut toujours amener son adversaire dans une configuration où le nimber est nul.
Reprenons le tableau. Au début, les pions sont en position 0, 1, 2 et 3. Leur nim-addition donne 0 : c'est une position perdante pour le premier joueur ! Imaginons que J1 avance le premier pion sur la case C1. Le nimber de la configuration est alors 2⊕1⊕2⊕3≠0. En déplaçant le 4eme pion en C4, on se retrouve dans une position nulle. J2 gagnera sans problèmes la partie !
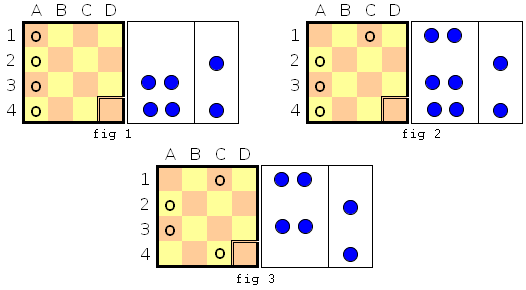
Exemple de début de partie, où J2 applique la stratégie gagnante.
fig 1 : J1 doit jouer, la configuration des pièces correspond à une configuration de Nim (0,1,2,3), de nim-addition nulle
fig 2 : J1 joue au hasard, il place son premier pion en C1. La configuration de Nim correspondante est (1,2,2,3), de nim-addition non nulle.
fig 3 : J2 rééquilibre la parité des colonnes du jeu de Nim, en déplaçant le 4eme pion en C4. La configuration de Nim correspondante est alors (1,2,2,1), la nim-addition est nulle.
Le jeu de Nim
Le jeu de Nim est l'exemple de base de jeu de graphe multi-pions. Une configuration comme (1,3,5) revient à jouer sur les tableaux suivants :
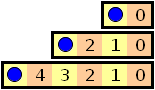
Chaque case représente le nombre de jetons restant dans une ligne. Le but du jeu est donc d'amener les 3 pions sur les 3 cases 0. Chose tout à fait étonnante (en fait, pas du tout), le nimber des cases est déjà écrit dans les cases ! La stratégie décrite pour gagner au jeu du graphe multi-pions est exactement la stratégie pour gagner à Nim : placer son adversaire dans une configuration de nimber (de nim-addition) nul ! Tout concorde !
Le jeu de Grundy
Le théorème de Sprague-Grundy peut s'avérer très utile dans les situations où le jeu se divise progressivement en plusieurs sous-jeux. L'exemple le frappant est celui du jeu de Grundy, qui se joue avec des piles de pièces. Chacun son tour, on doit choisir une pile, et la couper en deux piles de tailles inégales. Celui qui ne peut plus jouer perd.
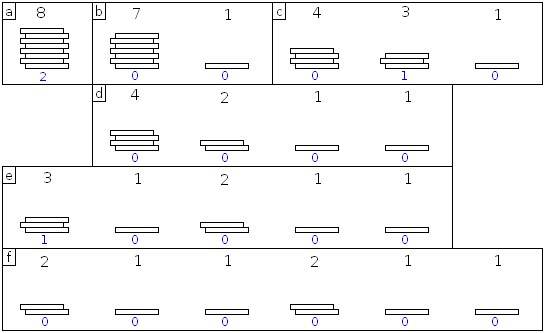
Exemple de partie de Grundy, menée d'une main de maître par J1. Les nombres en noir correspondent au nombre de pièces dans les piles, les nombre en bleu sont les nimber des tas.
a - Le jeu commence avec 8 pièces dans la pile
b - J1 sépare la pile de 8 en une pile de 7 et de 1
c - J2 sépare la pile de 7 en une pile de 4 et de 3
d - J1 sépare la pile de 3
e - J2 n'a pas le choix, et sépare la pile de 4
f - J1 sépare la dernière pile, et gagne
On s'intéresse alors au nimber d'une pile de taille n, que l'on va noter G(n).
Si n=1 ou n=2, on trouve que G(n)=0 (on ne peut décomposer ces piles en piles plus petites de taille inégale)
Si n=3, on peut découper la pile en 1 et 2, deux piles de nimber nul, donc de nim-addition nulle. Depuis une pile de taille 3, on ne peut arriver qu'en une configuration de nimber 0, on a donc G(3)=1.
Si n=4, on peut découper la pile en 1 et 3, qui est une configuration de nimber 1 (G(1) ⊕G(3)=1). On a donc G(4)=0.
⊕G(3)=1). On a donc G(4)=0.
Si n=5, on peut découper la pile en [1,4] (de nimber G(1)⊕G(4)=0) ou en [2,3] (de nimber G(2)⊕G(3)=1). On a donc G(5)=2 !

Tableau des premières valeurs de G(n)
Aujourd'hui, les valeurs de G(n) ont été calculées jusqu'à n=235, mais aucune régularité n'a encore été trouvée. Peut-être est-elle périodique, ou peut-être pas...
Quart de singe
Le jeu du quart de singe est avant tout un jeu de vocabulaire, mais il peut tout à fait rentrer dans la catégorie des jeux impartiaux. Prenons par exemple pour thème "Les animaux commençant par R". Il existe 46 animaux commençant par R (auquel on ne peut ajouter de lettre pour former un autre nom). Une fois tous passés en revue, on peut dire que celui qui commence gagnera la parti, il faudra toujours jouer les lettres de nimber 0 :

En rouge les lettres de nimber nul (cliquez pour agrandir)
Supposons que vous soyez le joueur qui commence : R (nimber 0)
Votre adversaire a le choix entre 6 lettres pour former un nom d'animal, il choisit le H : Rh (nimber 2)
Il pense au rhinocéros, ce qui le ferait gagner. Heureusement, il existe un cheval qui vous fera gagner : Rhé (nimber 0)
Votre adversaire s'incline !
Théoriquement, le quart de singe se joue sans thème, sur l'ensemble du dictionnaire... On pourrait facilement faire un programme qui gagnerait à presque tous les coups à ce jeu !
La clé de la réussite appartient à celui qui sait calculer un nimber
[proverbe polonais]
Sources :
Stratégies magiques au pays de Nim - Pour la science - n°377 - Mars 2009



/http%3A%2F%2Fstorage.canalblog.com%2F72%2F92%2F210892%2F113119539_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F00%2F91%2F210892%2F107069165_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F33%2F48%2F210892%2F101190494_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F83%2F38%2F210892%2F101168363_o.png)