Top 10 des maths animalières
Bientôt Noël ! On ne change pas une formule qui gagne. Après le top 10 des maths autour du monde -sur ce blog- ou le top 10 des nombres transcendants et irrationnels -sur d'autre blogs-, voici le top 10... des mathématiques animalière !
Ce top 10 vous est proposé dans un ordre aléatoire, sans aucune raison valable.
N° 7 : Le théorème et le lemme du papillon

Le théorème du papillon prétend que MX=MY
Deux triangles collés l'un à l'autre par un sommet, ça rappelle un papillon, non ? Il en faut peu pour baptiser un théorème ! Si trois cordes [AB], [CD] et [PQ] d'un cercle sont concourante en un point M qui est le milieu de [PQ], alors MX=MY, où X et Y sont les points d'intersection de (PQ) avec respectivement (AC) et (BD).
Le motif du papillon ne se retrouve pas qu'en géométrie. On parle aussi de lemme du papillon pour parler en algèbre du lemme Zassenhaus. Ce lemme, qui illustre une sombre histoire d'isomorphisme entre deux sous-groupe d'un Ω-groupe, s'illustre sous la forme d'un treillis qui ressemble à ce choupi papillon :

Diagramme de Hasse correspondant au lemme de Zassenhaus
N° 1 : Les lapins de Fibonacci, et celui de Douady

La suite de Fibonacci
La suite star des maths, célèbre pour ses liens trop étroits avec le nombre d'or, est la suite de Fibonacci. On commence par 0 et 1, et les termes qui suivent s'obtiennent en additionnant les deux termes précédents. Ceci donne 0, 1, 1, 2, 3, 5, 8, 13,... Les origines de cette suite, et son rapport avec Pan-Pan, remontent au XIIIe siècle, sous la plume de Leonardo Fibonacci : un problème récréatif sur la procréation incessante d'une population de lapins :
" Un cuniculteur élève un couple de lapereaux. Il s'aperçoit qu'un couple devient adulte après 3 mois, et qu'une fois adulte, un couple de lapin met tous les mois au monde un nouveau couple de bébés lapin. Sachant qu'un lapin ne meurt jamais, combien aura-t-il de couples après 1 an ? "
En détaillant le nombre de couples que l'on a mois après mois, on se retrouve face à une suite de Fibonacci, ce qui résout le problème posé.
Il y a aussi la suite du lapin, obtenu en partant de 0, et en transformant à chaque étape 0 par 1 (le lapin devient adulte) et 1 par 10 (le lapin engendre un nouveau lapin). La suite donne donc 0, 1, 10, 101, 10110, 10110101, ... En poursuivant à l'infini, on obtient le développant binaire du nombre 0,10110101... (en décimal, R=0.7098034...), appelé nombre du lapin. En cherchant un peu, on lui trouve des liens avec la suite de Fibonacci ou évidemment le nombre d'or.
Et sinon, il y a le lapin de Douady, qui est la fractale de Julia que l'on obtient en prenant le paramètre c = -0.123 + i.0.745, et qui ressemble, de loin dans le brouillard, à un lapin :

Le lapin de Douady (à peu de chose près)
N° 5 : Le lemme du serpent

Diagramme du lemme du serpent, où le serpent est le morphisme d, en bleu.
Étant donné un diagramme commutatif qui ressemble à ce qu'il doit ressembler, on en déduit une suite exacte faisant intervenir les noyaux et les conoyaux. De la chasse au diagramme dans toute sa splendeur, que l'on appelle le lemme du serpent. Pourquoi un serpent ? Par que ce lemme promet l'existence d'un morphisme qui, graphiquement, ressemble à un serpent. Il faut remercier l'équipe Bourbaki (cocorico !) pour ce chouette nom de baptême.
N° 4 : La loi de Poisson, les fonctions de Morse, la formule de Héron, le théorème de la Vallée-Poussin...
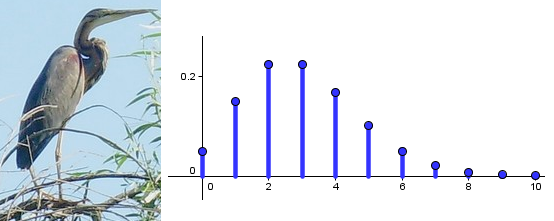
Un héron qui surveille une loi de Poisson...
En proba, on parle de la loi de Poisson. En topologie différentielle, on déconstruit les surfaces à l'aide de fonctions de Morse. En géométrie euclidienne, la formule de Héron donne l'aire d'un triangle à partir de la longueur de ses côtés. En théorie des nombres, le théorème De la Vallée Poussin donne une approximation sur la croissance des nombres premiers...
Malheureusement, tout ça n'a rien à voir avec Polochon, Rotor Walrus, Sinker ou Caliméro. C'est simplement que ces théorèmes tiennent leur nom de Siméon Denis Poisson (1781-1840), de Marston Morse (1892-1977), de Héron d'Alexandrie (Ier siècle) ou de Charles-Jean Étienne Gustave Nicolas Levieux, baron de la Vallée Poussin (1866 - 1962)...
N° 3 : Les algorithmes de colonies de fourmis

Comment trouver le chemin le plus court (à vol d'oiseau) qui passe Paris, Lyon, Marseille, Lille, Toulouse, Bordeaux, Nice, Nantes, Strasbourg et Toulon ? C'est le le problème du voyageur de commerce, réputé sa difficulté à être résolu. Il existe cependant plusieurs algorithmes, chacun ayant leur efficacité, pour le résoudre, dont l'algorithme de la colonie de fourmis, qui se calque sur les méthodes employés par les fourmis pour trouver le plus court chemin entre la fourmilière et une source de nourriture.
Pour cela, on récupère une colonie de fourmis artificielle prête à voyager à travers la France. Chaque fourmi passera par chacune des dix villes, en lâchant sur son passage des phéromones, et en choisissant son chemin de manière aléatoire en empruntant de préférence les chemins les plus courts et les plus chargés en phéromones. La quantité de phéromone lâchée par une fourmi sera proportionnelle à l'intérêt du voyage (beaucoup de phéromones pour un voyage court, et inversement). Au cours du temps, les phéromones s'évaporent, et seuls les chemins les plus intéressant resteront plus marqués. Ainsi, les premières fourmis, les éclaireuses, choisiront leur chemin avec beaucoup de hasard, mais les dernières fourmis prendront les chemins les plus marqués en phéromone, donc les plus intéressants.
N° 10 : Le graphe criquet

A droite, le graphe criquet ; a gauche, un criquet. Ou l'inverse. Je n'arrive plus à distinguer les deux tellement ils se ressemblent !
Le graphe criquet, c'est un graphe. Qui a vaguement la forme d'un criquet. Faut pas chercher plus loin...
En fait, c'est le nom officiel de ce graphe à 5 sommets et 5 arrêtes, donné par l'ISGCI (Information System on Graph Class Inclusions). Parmi les autres graphes ayant un petit nom animalier, on trouve le graphe poisson, le graphe papillon, le graphe mite, le graphe taureau ou le graphe longhorn...

Le poisson, le papillon, la mite,
le taureau et le longhorn
N° 8 : Le principe des cases à pigeons

10 pigeons, 9 cases...
Si on range 6 paires de chaussettes dans une commode à 5 tiroirs, alors l'un des tiroirs recevra au moins deux paires de chaussettes. Si un pigeonnier de 10 cases comporte 42 pigeons, alors l'une des cases comporte forcément au moins 5 pigeons...
C'est le principe des cases à pigeon (pigeonhole principle), ou, comme on l'appelle plutôt en français, le principe des tiroirs (de Dirichlet(-Schläfli)). Si n tiroirs sont occupés par k.n+1 objets, alors l'un des tiroirs possède au moins k+1 objets. Bref : on ne peut pas trouver d'injection partant d'un ensemble vers un ensemble plus petit... C'est le théorème de base de la théorie des ensembles, et que l'on peut utiliser sans compter dans des problèmes de dénombrement comme "prouvez que, en France, il y a à tout moment au moins 60 personnes qui possèdent exactement le même nombre de cheveux".
N° 2 : Les castors affairés

Après 107 étapes, ce castor affairé écrit sur la bande
. . . 0 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 . . .
Une machine de Turing est une machine virtuelle composée d'un ruban d'une infinité de cases, remplies de 0 ou de 1 ; d'une tête de lecture/écriture qui sait se déplacer, réécrire des 1 ou des 0 dans les cases ; d'une table d'actions ; d'un ensemble fini d'états {A, B, ...} possibles. La tête de lecture suit exactement les instructions de la table qui ressemblent à quelque chose comme "si on est dans l'état A et que le caractère lu est un 1, alors on réécrit un 0, on déplace la tête vers la droite et on se place dans l'état B" ou "si on est dans l'état B et que le caractère lu est un 0, alors on s'arrête". Ce prototype de machine est la base théorique de tout programme informatique. Un jeu proposé par le mathématicien hongrois Tibor Radó est de trouver la machine de Turing à n états qui dure le plus longtemps. C'est le n-ième castor affairé ! (Faut imaginer un castor totalement dévoué à la cause des machines de Turing qui passerait ses journées à déplacer ses noisettes)
Un n-castor affairé est donc une machine de Turing à n états qui, à partir d'un ruban vierge, écrit un maximum de 1 (mais qui s'arrête tout de même). De manière à peu près équivalente, le n-castor affairé d'un langage informatique donné est le programme de n caractères qui écrit le plus grand nombre possible. Par exemple, le castor affairé à 4 états s'arrête après 107 étapes, et après avoir écrit 13 "1". En pratique, trouver un castor affairé est quelque chose de très difficile, puisqu'il faut étudier cas par cas toutes les machines de Turing possibles à n états pour voir si elles s'arrêtent un jour, et au bout de combien d'étapes (c'est faisable, mais vite compliqué dès lors que n est grand, voire humainement impossible pour pour n>10). En théorie, trouver un castor affairé est tout simplement impossible : il faudrait trouver un programme capable de dire si un programme donné s'arrête ou non, ce qui serait paradoxal...
N° 6 : Le théorème du nid d'abeille

Le pavage du plan le plus économique en cire !
Pour stocker leur miel, leurs œufs ou d'autres trucs, les abeilles doivent faire face à un problème de taille lorsqu'elles construisent leurs alvéoles : quelle forme utiliser ? Leur instinct répond à leur place : les alvéoles en forme d'hexagone sont ce qu'il y a de plus malin, puisque c'est le pavage régulier le plus économique en terme de périmètre qui existe (et donc, pour une abeille, celui qui économise au plus la cire).
Le théorème du nid d'abeille pose donc la question du pavage du plan par des tuiles égales ayant le plus petit périmètre possible (pour une aire donnée). Si on se limite aux tuiles en forme de polygones réguliers, on trouve 3 tuiles possibles : les tuiles carrées, triangulaires ou hexagonale. Quelques calculs suffisent à montrer que la tuile hexagonale est le meilleur choix.
Mais pourquoi devrait-on à tout prix utiliser des tuiles régulières. On peut parfaitement paver le plan avec des tuiles en forme de parallélogramme, par exemple ! Il y a alors une infinité de tuiles possibles, ce qui complique considérablement les choses. Le problème est très ancien (on le retrouve dans les traités mathématiques antiques), et a été considéré par beaucoup comme l'un des plus grands problèmes de la géométrie. Après plusieurs siècles de travail, le CQFD final de la démonstration a été écrit en 1999, sous le bic de Thomas Hales (qui a aussi résolu la conjecture de Kepler).
N° 9 : La selle de cheval et la selle de singe

A gauche, une selle de cheval, d'équation z=x²+y²
A droite, une selle de singe, d'équation z=x(x²-2y²)
En géométrie différentielle (et d'autres domaines), on préfère ne pas parler de "paraboloïde hyperbolique", mais plutôt de "selle de cheval", qui chatouille un peu plus l'imagination ! Le centre de la selle de cheval est à la fois un minimum et un maximum, suivant le plan dans lequel il est coupé.
Il existe plus tordu : la selle de singe (une selle sur laquelle peut se poser un singe de manière à avoir de la place pour ses jambes et pour sa queue). Le centre de cette selle n'est jamais un maximum ni un minimum quand on le coupe par un plan sécant...
Sources :
La plupart des photos sont l'œuvre de ma camarade Miss Grelot, du blog macrophotophile Zygena.
Les autres images, c'est du wikipédia : Butterfly lemma, Pigeonhole principle.



/http%3A%2F%2Fstorage.canalblog.com%2F72%2F92%2F210892%2F113119539_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F00%2F91%2F210892%2F107069165_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F33%2F48%2F210892%2F101190494_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F83%2F38%2F210892%2F101168363_o.png)