Réglons une bonne fois pour toute cette histoire de nombre d'or

Selon une étude, les rectangles dont le format suit le nombre d'or seraient les plus beaux/harmonieux/attirants (rayez la mention inutile) de tous les rectangles. Peut-être, mais il m'en faut plus pour pouvoir être vraiment convaincu. Et si on étudiait vraiment cette question ? Faisons de la science !

Formats de rectangles
Avant de parler de rectangle d'or ou de choses du genre, donnons quelques généralités. On appelle format f d'un rectangle le rapport entre la longueur de son plus grand côté (L) et de son plus petit côté (l). C'est donc un nombre qui sera supérieur à 1 (ou égal à 1 dans le cas d'un carré).

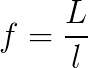
L'intérêt de cette notion, c'est que si deux rectangles ont le même format, alors ils sont grosso modo identiques (ils sont superposables moyennant un agrandissement ou une réduction). Un rectangle de format 1.4, c'est un rectangle 1.4 fois plus long que large, quelle que soit sa taille ou son orientation.

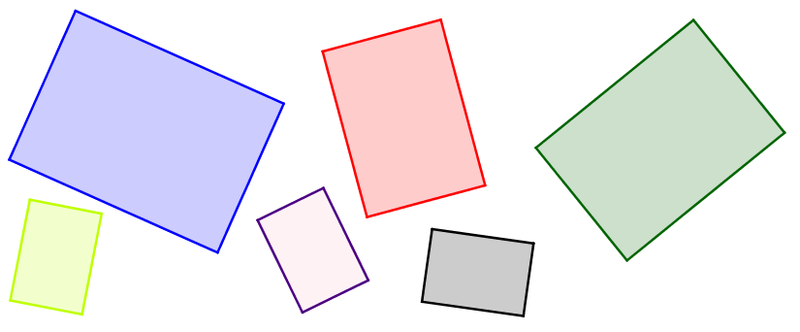
Tous ces rectangles sont similaires : ils ont le même format, malgré une taille et une orientation différente.

Petit panorama des différents formats que l'on a l'habitude d'avoir sous les yeux.

Petit panorama des formats de rectangles que l'on croise dans la vie quotidienne.
Les points violets sont les formats testés dans le sondage décrit plus bas.

Quelques précisions sur les formats de la vie quotidienne

• Le format des peintures les plus célèbre est loin d'être fixe, de 1.26 pour la nuit étoilée de Van Gogh jusqu'à 2.22 pour Guernica. J'aurais pu placer le radeau de la méduse (1.45) ou la Cène (1.91)
• Mis à part Macron qui fait son malin avec une photo officiel au format 1.4, les autres présidents de la 5e république ont en mairie des photos au format 1.3.
• La norme ID-1 donnant le format des cartes de crédit a lui permet de se rapprocher du nombre d'or (1.6). Du côté des autres cartes, nos cartes d'dientités françaises (norme ID-2) ont pour format 1.41, tout comme les passeports (norme ID-3). Les cartes SIM utilisent le format 5/3 (norme ID-000).
• Les billets de banques ont des formats assez longs ; de 1.8 pour le billet de 20€ jusqu'à 1.95 pour le billet de 500€.

Mathématiquement, il y a deux formats qui sont un peu plus intéressants que les autres :

• le format f = √2, plus connu sous le nom A4 ou A3. C'est le format des cartes postales, de votre fiche de paie ou des cartes de poker. Il repose sur une construction mathématique : il faut que, lorsque l'on plie en deux une feuille de format Ax, on obtienne une feuille de même format. Théorème : il n'y a qu'un seul format qui vérifie cette propriété.
  
  Posons l'équation. On prend un rectangle de longueur L et de largeur l (on supposera L>l) ; son format est donc f = L/l. On plie ce rectangle en deux : la nouvelle longueur L' est l'ancienne largeur, donc L'=l, et la nouvelle largeur l' est la moitié de l'ancienne longueur, donc l'=L/2. Le nouveau format est donc f' = L'/l' = l/(L/2) = 2/f. Ces deux formats doivent être les mêmes ce qui donne l'équation f=f', soit f=2/f, et donc f²=2. Cette équation n'a qu'une seule solution (positive) : f = √2.
  
  Dans un souci de standardisation, il a aussi été décidé qu'une feuille de format* A0 mesurerait 1m² ; puisqu'elle doit être √2 fois plus longue que large, cela donne à la feuille A0 des dimensions de 841mm x 1189 mm. Bref, si nos feuilles d'impots nous sont proposées au format f ≈ 1.41, c'est pour qu'une fois pliée en 2, elle ressemble encore à cette même feuille d'impot.
  * Parler de "format" A0 est un abus de langage, puisque des feuilles de dimensions A0, A3 ou A4 ont leur format, au sens mathématique, identique.
  
  
• Le format f = φ, où φ = (1+√5)/2 ≈ 1.62 est le nombre d'or. Ce format repose lui aussi sur une construction géométrique, un peu plus alambiquée que pour le format précédent. L'idée est de chercher s'il existe un rectangle qui conserve son format lorsqu'on lui retire un carré. Théorème : il n'y a qu'un seul format qui vérifie cette propriété.
  
  On peut une nouvelle fois le mettre en équation. On part une nouvelle fois d'un rectangle de dimension L×l (on supposera L>l), donc de format f = L/l. On retire un carré de côté l. La pièce restante est un rectangle, de longueur L' = l et de largeur l'=L-l ; son format est donc f' = L'/l' = l/(L-l) = 1/(f-1). Le grand et le petit rectangle ont le même format, donc f'=f, soit f = 1/(f-1), et donc f² - f = 1. Cette équation n'a qu'une unique solution positive : f = (1+√5)/2.
  
  Le format f = φ donnant le rectangle d'or est donc issu d'une construction géométrique, mais ne répond pas à une problématique autre que la satisfaction de faire des maths. On ne retrouve pas dans la vie quotidienne de rectangle ayant ce format à cause de cette considération géométrique. En particulier, c'est un hasard que nos cartes bleueus aient ce format ; si on avait voulu le faire volontairement, cela aurait été bien plus précis.

La grande étude
Il semble pourtant, à en croire les sites internet complotistes ou new age, que le format d'or est partout, parce qu'il correspondrait à un idéal esthétique. Les arguments employés se basent en général sur des appels à la tradition (les grecs utilisaient le nombre d'or, donc c'est vrai) ou d'appel à la nature (on trouve le nombre d'or dans la nature, donc c'est vrai). Quand on recherche la présence de rectangles d'or dans des peintures ou des sculptures que l'on juge esthétiques, on le retrouve, ce qui permettrait de confirmer l'hypothèse "nombre d'or = c'est bô". Le principal problème, c'est que si l'on cherche des rectangles ayant d'autres formats dans ces mêmes peintures et sculptures, on les retrouvera également.

Certes, mais au final, peut-être que les rectangles d'or sont effectivement préférés aux autres rectangles ? Pour en avoir le cœur net, il faut étudier scientifiquement la question, et heureusement, de nombreux psychologues l'ont fait avant moi.

La première étude emblématique de la question est celle du psychologue allemand, Gustav Fechner, en 1874. C'est d'ailleurs sur cette étude que s'appuient les pro rectangle d'or.  Il présente à ses sujets 10 rectangles, allant du format f=1 jusqu'à f=2.5, chacun d'aire égale. Ceux-ci sont blancs, posés sur un tableau noir, et rangés dans l'ordre de leur format. Leur orientation n'est pas connue. Fechner demande au sujet de choisir LE rectangle qu'ils préfèrent, et celui qu'ils aiment le moins. Le rectangle d'or (f = 1.62) est placé en 7e position, entre le format f=1.5 et le format f=16/9. Sur ses 347 réponses, 35% ont préféré le nombre d'or, 20.6% ont préféré le format f=1.5, et 20% pour le format f=16/9. Au contraire, personne n'a choisi le rectangle d'or comme rectangle le moins aimé, et seulement 1.4% ont choisi un des deux rectangles adjacents.

Fechner ne s'est pas arrêté aux rectangles. Il a aussi testé, sous le même protocole, les préférences pour les ellipses. Cette fois-ci, c'est l'ellipse de format f=1.5 qui a eu la préférence (à 42%) des sujets, contre seulement 16.7% pour l'ellipse d'or.
Il a également compilé le format de 20 000 peintures provenant de différents musées et galleries d'art. Le format f=5/4 est privilégié pour les peintures en orientation portrait, et f=4/3 pour celle d'orientation paysage.

Depuis Fechner, de nombreux psychologues ont étudié la question, en variant les protocoles expérimentaux. En 1995, le psychologue canadien Christopher Green a compilé une quarantaine d'études, de 1874 jusqu'à 1992. Les différents résultats sont loins d'être unanimes. Bien qu'ils tournent pour la plupart autour de f=1.6, la préférence n'est jamais très marquée, et jamais précisément sur le rapport d'or.

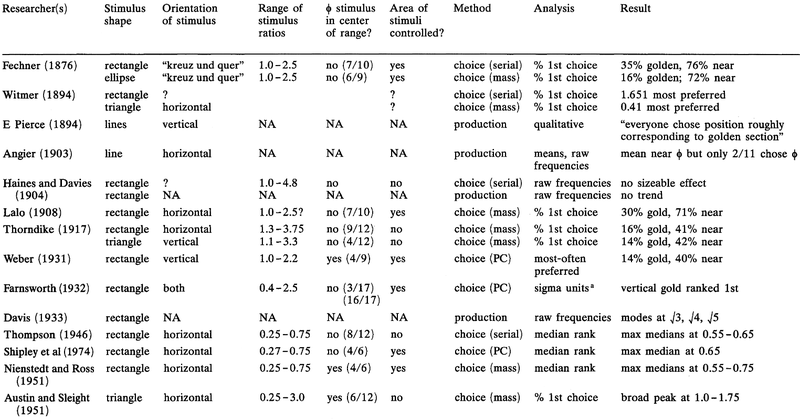
Du coup, j'ai eu envie de tester moi aussi l'hypothèse, en proposant aux internautes qui me suivent sur Twitter et Facebook de noter des rectangles. Les meilleures notes sont-elles attribuées au rectangle d'or ? Nous allons le voir tout de suite.

J'ai donc proposé aux volontaires de note 20 rectangles de 0 (non harmonique) jusqu'à 5 (très harmonique). Les rectangles sont proposés dans un ordre aléatoire, les volontaires ont été libres de ne pas donner de notes à tous les rectangles. Chaque rectangle (sauf le carré) est présenté en trois exemplaires : en orientation portrait, paysage, et après une rotation de 24°. Tous les rectangles sont de la même couleur, chacun est inscrit dans un cercle de même taille (les aires ne sont cependant pas toutes identiques).

• Deux carrés (rectangle de format f = 1)
  
• Trois rectangles de format f = 4/3 ≈ 1.33
  
• Trois rectangles de format f = √2 ≈ 1.41
  
  
  
• Trois rectangles de format f = φ ≈ 1.62
  
  
  
• Trois rectangles de format f = 16/9 ≈ 1.78
  
• Trois rectangles de format f = 2
  

Je regrette de ne pas avoir glissé de rectangle de format 1.5...

Les résultats
Passons sans plus attendre aux résultats. Merci aux 772 personnes qui ont répondu. Comment avez-vous noté tous ces rectangles ? Voici les résultats bruts. Je vous laisse dans les sources mes données brutes, que vous puissiez vous aussi faire joujou avec.

Distribution des notes proposées

Quand on regarde la proportion de 5/5, le rectangle jugé le plus harmonique semble être le carré, dépassant de peu le rectangle d'or (f=1.62)  orienté paysage, et le rectangle 16/9 (f=1.78) orientation paysage. De manière générale, vous préférez toujours les formats paysages aux autres formats.
Si on s'intéresse aux rectangles jugés à au moins 4/5, le rectangle d'or (paysage) et le rectangle 16/9 (paysage) passent devant.

Au rayon des rectangles les plus rejetés, le prix revient également au carré, quelle que soit sa forme. Le carré est donc à la fois le plus apprécié et le plus déprécié. Le format f=2 à la verticale semble également particulièrement repoussant.

Distribution des meilleures notes données, accompagnée de son intervalle de confiance à 95%.
Une même meilleure note peut être attribuée à plusieurs rectangles différents.

Sur ce critère, les résultats sont similaires. Le rectangle d'or (paysage) arrive en tête (37% des votes), suivi du carré (31.3%), puis du rectangle 16/9 (29.5% des votes). De tous les formats portraits (hors carré), le format √2 est le premier.

Note moyenne et écart-type attribués à chaque rectangle

Lorsque les rectangles sont présentés en orientation paysage, le rectangle d'or et le rectangle 16/9 arrivent pour ce critère une nouvelle fois en première position. En orientation portrait, ce sont cependant les formats √2 et 4/3 qui ont vos préférences.

Finalement, l'expérience semble dire que de tous les rectangles qui vous ont été proposés, ce sont le rectangle d'or en format paysage et le carré posé que vous avez plébiscité. Ça pourrait être un résultat intéressant, mais il y a quand même plusieurs soucis. Déjà, les préférences pour un format donné sous l'orientation paysage ne se retrouvent pas dès que celle-ci est changée ; le rectangle d'or est apprécié en paysage mais boudé en portrait. De plus, mon questionnaire s'est limité à un échantillon de seulement 6 rectangles différents, ce que l'on pourrait sans doute affiner davantage. Un questionnaire avec des rectangles générés automatiquement serait parfait. Enfin, il y a un certain biais dans la population testée, certains ayant avoué avoir voté pour le rectangle d'or parce que c'est le rectangle d'or.

Bref, je ne sais pas si j'ai fait avancer la science, mais on a au moins une réponse. Une réponse floue, mais c'est quand même une réponse.

---

Sources :
All that glitters : a review of psychological research on the aesthetics of the golden section, Christopher D. Green
Faites vos propres stats : les données brutes

Comments

[b1a2s3a4l5t6e7]

(1 + .68)/1 = 1/(.618)



Moi je retient le carré dans un rectangle d'or;

Aussi un carré dans un cercle ayant comme diamètre la diagonale de ce carré, je remarque que la circonférence moins la sommes des deux diagonales donne 1.614456 coté du carré. Il faudrait donc donné une épaisseur infime au cercle pour obtenir le nombre d'or exact, référence;

https://gnralsujet58.blogspot.com

[ylvekio]

une BONNE fois pour toutes ! c'est-y pas un pléonasme , des fois...?

[Gerbille]

Au bridge, en match par 4, on marque des IMPs ou "international match points" ; ces IMPs sont ensuite convertis en Points de Victoire par une formule qui a changé il y deux ans environs ; celui qui a proposé la nouvelle formule y a introduit le nombre d'or, surement pour se faire plaisir !

Pour info, ce WE (du 27 au 27 août) l'équipe de France rencontre une équipe américaine en finale du championnat du monde à Lyon.

[Jer]

Visuellement, qui peut faire la différence entre le nombre d'or et, disons, 5/3 ou 8/5 ?

[amic]

Sur quoi étaient affichés ces rectangles ?

Dans la majorité sur un écran d’ordi (paysage) ou d’intelliphone (portrait, paysage ?).



J’imagine que ça biaise aussi le test… on juge le rectangle par rapport au cadre dans lequel il est présenté…