De l'autre côté du miroir (et ce que Euclide y a trouvé)
Le journal Le Monde, avec l'assentiment de Cédric Villani, vient de lancer "Le monde est mathématique", une série de 40 ouvrages vulgarisant l'ensemble des mathématiques. Il s'agit en fait d'une réédition revue et corrigée de la même série sortie en août 2011.
 Le nombre d'or : le langage mathématique de la beauté
Le nombre d'or : le langage mathématique de la beauté
~~~~~~
Pour le numéro 1, ils ont choisi le sujet qui domine les mathématiques, le phénomène qui explique la beauté du monde qui nous entoure, de la nature à l'architecture en passant par l'astronomie. Aussi incroyable que cela puisse paraître, un simple nombre régit l'Univers et l'esthétisme : le nombre d'or ! Qu'on l'appelle "divine proportion", "chiffre d'or", "ratio pimpant" ou Φ, on fait toujours référence à ce nombre qui régit l'agencement des pétales des tulipes, de la forme des galaxies ou de l'ensemble des productions artistiques depuis la Renaissance italienne. Bref, un excellent choix pour un premier numéro, qui laisse présager d'une excellente série !
Les origines du nombre d'or
Les origines du nombre d'or remontent à l'antiquité, lorsque Euclide écrit dans son livre XLII :
"Un rectangle est dit coupé en extrême et moyenne raison quand, comme le plus grand côté est au plus petit, ainsi est le plus petit relativement à la moitié plus grand "
Le nombre d'or prendra ses lettres de noblesse à la Renaissance lorsque Luca Pacioli le met à l'honneur De divina proportionne, illustré par Léonard de Vinci himself ! Puisque ce rectangle en extrême et moyenne raison est l'oeuvre de Dieu, il devient pour la première fois "divin". La renommée du nombre d'or aujourd'hui est due aux travaux sur l'esthétisme du philosophe allemand Adolf Zeising, qui montre que tout ce qui est lié au beau est également lié au ratio d'or. Il prend alors le nom Φ (phi), en référence à Phidias, le sculpteur du Parthénon.
Géométriquement, cela revient à déterminer la proportion a/b qui vérifie :
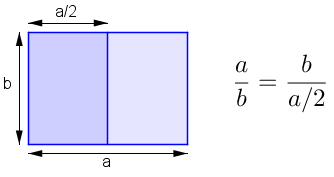
Algébriquement, on peut calculer la valeur de Φ :
![]()
Le nombre d'or est également lié aux suites de Fibonacci, deux suites (pn) et (qn) où chaque terme est obtenu en ajoutant les termes des rangs précédents : pn = pn-1 + qn-1 et qn = 2pn-1 + qn-1. En démarrant les suites à 1, on obtient :
(pn) : 1, 2, 5, 12, 29, 70, 169, 408
(qn) : 1, 3, 7, 17, 41, 99, 239, 577
La particularité de cette suite, c'est que les quotients des termes de même rang se rapprochent de Φ !
![]()
Le nombre d'or dans la nature
Considérer le nombre d'or comme l'étalon de la beauté n'a rien d'arbitraire, la nature offrant son lot d'exemples pour le confirmer. Pour les débusquer, on a besoin de ces outils que sont le rectangle d'or, le triangle d'or, la spirale d'or ou l'ellipse d'or :
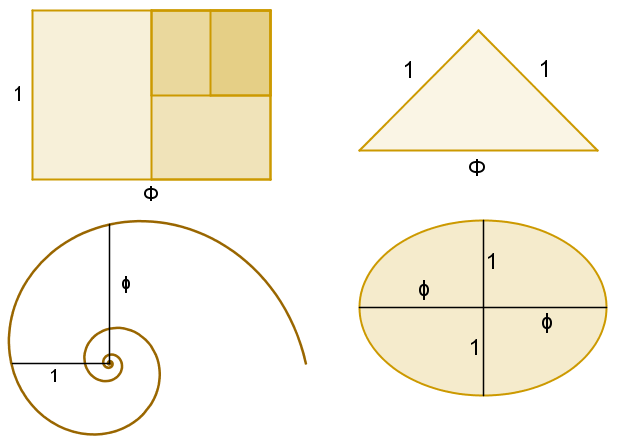 Si ces formes vous semblent familières, c'est qu'elles sont le langage de la nature !
Si ces formes vous semblent familières, c'est qu'elles sont le langage de la nature !
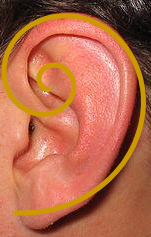
La spirale d'or permet de repérer le nombre d'or dans le coquille d'un nautile, dans le bras d'une galaxie, dans le pavillon d'une oreille ou dans les spirales des feuilles d'aloès :
Le nombre d'or dans l'architecture
Le nombre d'or trouve évidemment ses origine dans les plans du Parthénon, qui s'inscrit dans un rectangle d'or parfait, mais on le retrouve dans de nombreux monuments. Par exemple, le nombre d'or apparaît dans la Tour Eiffel, dans la grande mosquée de Kairouan ou dans le dolmen de Crucono :
Le nombre d'or dans l'art
Le nombre d'or se retrouve naturellement dans de nombreuses oeuvres d'art, que ce soit dans la Joconde ou dans l'École d'Athène. On pourrait multiplier ces exemples chez la plupart des artistes, de la période hellénistique grecque au Pop Art moderne, en passant par l'art Byzantin ou le néo-classicisme.
Attention cependant, le rectangle encadrant l'homme de Vitruve de De Vinci n'est pas un rectangle d'or, mais la page sur lequel il est dessiné possède bien ces proportions. Puisque je vous dis que le nombre d'or est partout !
Bref, si la nature possède un cadenas à sa compréhension, le nombre d'or Φ = 1.414... ne peut qu'en être sa clé !
Images :
Nautilus Cutaway Logarithmic Spiral, Ear, Aloe polyphylla spiral, 2006 01 21 Athènes Parthénon, Galerie mosquée Kairouan, Crucono Dolmen
Vous l'aurez évidemment compris, cet article est un hilarant poisson d'avril. Pour de vraies informations sur le nombre d'or, retournez là-bas.












/http%3A%2F%2Fstorage.canalblog.com%2F82%2F99%2F210892%2F116837441_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F11%2F12%2F210892%2F104995347_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F42%2F88%2F210892%2F71308477_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F67%2F62%2F210892%2F68963066_o.png)