Miction impossible
Les mathématiciens traitent de sujets graves, comme lorsqu'ils s'interrogent sur les bornes inférieures et supérieures de la première valeur propre d'un opérateur de diffusion non-locales (1). Les mathématiciens s'occupent de sujets difficiles, comme celui du théorème de Schur-Horn pour les opérateurs à spectre fini (1). Mais les mathématiciens s'occupent surtout de sujets fondamentaux, comme celui du meilleur choix possible dans une rangée d'urinoirs (2).
Oui, ça faisait longtemps que ce blog n'avait pas eu de nouveau billet. Surtout que je me contente aujourd'hui de reprendre la dernière entrée de chez Globule et télescope. Mais n'oublions pas que ce 19 novembre, c'était la journée mondiale des toilettes, et que ce genre d'événement n'arrive qu'une seule fois dans l'année.
C'est donc avec le plus grand sérieux que deux mathématiciens (l'un canadien, l'autre américain), ont mis à profit leur génie pour répondre à la question suivante :
Étant donné une rangée d'urinoirs, lequel faut-il choisir pour maximiser le maintien de son intimité ?
Autrement dit, quel urinoir choisir pour minimiser la probabilité que quelqu’un choisisse l'urinoir d'à-côté ? Evangelos Kranakis et Danny Krizanc proposent, dans un papier de 12 pages, plusieurs éléments de réponses.
Considérons donc des toilettes classiques : une seule rangée de n urinoirs, la porte d'entrée d'un côté, le mur de l'autre. La situation est la suivante : vous êtes le premier à entrer dans ces toilettes pour un besoin pressant. On suppose également que les urinoirs sont propres. Alors, quel urinoir choisir pour une miction pérenne ?

21 urinoirs, un seul bon choix... Lequel ?!
L'instinct indique que le meilleur choix possible est l'urinoir le plus éloigné de la porte. Ainsi, si quelqu’un d'autre passe la porte des WC messieurs, il devrait choisir l'urinoir opposé, vous permettant de finir tranquillou ce que vous avez si bien commencé. Mais pour en être vraiment sûr, il faut modéliser le problème !
Dans ce modèle, nous considérerons que tout homme a ses besoins d'intimité. A moins d'y être obligé, aucun homme ne cherchera à être voisin d'un urinoir occupé. Si il y est contraint, on dira que les toilettes sont "saturées". Votre choix est primordial : il faut maximiser le temps avant la saturation ! On dit qu'un urinoir est "privé" si les deux urinoirs d'à côté sont libres.
Premier modèle : l'homme est paresseux
Pour ce premier modèle, on suppose qu'un homme entrant dans les toilettes prendra le premier urinoir privé disponible, celui le plus proche de la porte. Si le nombre n d'urinoir est pair, la configuration saturée est celle où la moitié des urinoirs sont occupés (n/2 urinoirs occupés : ceux de rang impair). Remarquons alors que le choix de l'urinoir que vous ferez (qu'il soit de rang pair ou impair) n'aura aucune incidence sur le temps de saturation.

Exemple avec 10 urinoirs : que vous choisissiez le septième ou le huitième, seule 4 personnes pourrons venir avant que les toilettes soient saturées.
Dans le cas où le nombre n d'urinoirs est impair, il ne faut impérativement choisir un urinoir de rang impair. Dans ce cas, la saturation arrivera à (n+1)/2 urinoirs occupés, au lieu de (n-1)/2 !
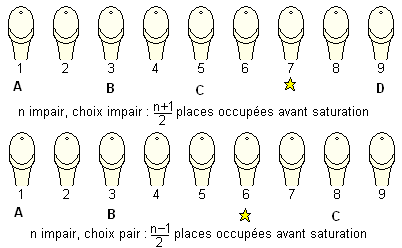
Exemple avec 9 urinoirs : si vous choisissiez le septième, 4 personnes pourrons venir avant que les toilettes soient saturées, elles satureront au bout de 3 si vous choisissez le sixième.
Remarquons que, une fois que les toilettes sont saturées, les nouveaux arriveront choisiront au hasard l'un des urinoirs disponibles. Pour minimiser la probabilité d'avoir un voisin de courtoisie, le mieux est de minimiser le nombre d'urinoirs voisins libres. Le meilleur choix est donc de prendre un des emplacements extrême (un seul voisin possible). Résumons ceci par des équations : si vous choisissez l'urinoir 1 ou n, le temps moyen avant d'être dérangé sera proportionnel à
![]()
et si vous choisissez un autre urinoir, le temps d'attente sera proportionnel à
![]()
Le choix est donc vite fait : les urinoirs extrémaux sont les plus sûrs !
Deuxième modèle : l'homme est pudique
Dans ce deuxième modèle, le nouvel entrant ne cherche pas à prendre le premier urinoir privé qu'il rencontre, mais cherche à maximiser la distance qui le sépare de l'homme le plus proche. Si plusieurs urinoirs maximisent la distance de sécurité, le choix est fait au hasard.
Remarquons que, quel que soit le choix que vous ferez, le prochain homme qui entrera choisira un urinoir extrémal. Appellons A(n,i) le nombre d'hommes pouvant entrer dans les toilettes avant qu'elles ne soient saturées si il y a n urinoirs et que vous choisissez le i-ème. Pour des raisons de symétrie, ce nombre est défini sans ambiguïtés.
Par exemple, pour 12 urinoirs, si vous choisissez le premier, 4 autres individus pourront venir alors que si vous choisissez le troisième, vous pourrez accueillir un homme en plus.
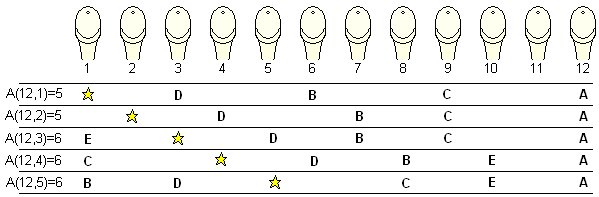
Expérimentalement, on peut calculer quelques valeurs de A. Ici, on voir queA(12,1)=A(12,2)=5, alors que A(12,3)=A(12,4)=6.
Avec un peu de méthode, on peut trouver l'expression de A(n,i) :
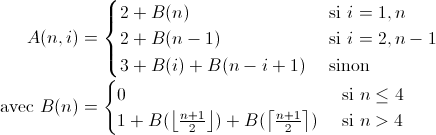
Ici, B(n) correspond au nombre d'homme nécéssaire pour saturer une rangée de n urinoirs lorsque les deux urinoirs extrémaux sont occupés.
La fonction B peut être explicitée (avec plein de logarithmes et de parties entières), mais il n'y a pas de formule donnant le i qui maximise A(n,i). Un détail : choisir un urinoir extrémal ne que rarement le choix optimal. Du coup, pour choisir le meilleur emplacement, il faut venir aux toilettes avec un ordinateur...
Allez, je suis beau joueur, je vous donne les meilleurs spots pour les plus petites toilettes (les petites valeurs de n) :
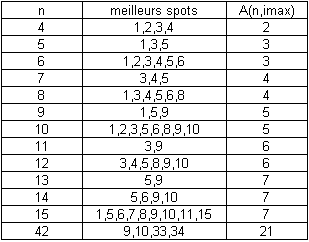
Tableau récapitulatif des meilleurs emplacements
Troisième modèle : l'homme est bourré
On peut également expérimenter un troisième modèle : un homme qui entre dans les toilettes cherche simplement un urinoir sans voisins, rien de plus. Son choix se fera uniformément parmi les urinoirs privés disponibles. Si aucun urinoir privé n'est disponible, il en choisira un au hasard parmi ceux restant.
Dans ce troisième modèle, les calculs sont un peu plus complexes, mais la conclusion est la même que pour le premier modèle : le meilleur choix est le choix de l'urinoir extrémal !
De nombreuses variantes peuvent être apportées au problème initial. On peut, par exemple, introduire la notion d'urinoir "semi-privé" (seulement 1 voisin) : à choisir, un homme préfère avoir un voisin plutôt que deux ! Il faut également réfléchir au cas où vous n'êtes pas le premier à entrer dans les toilettes (situation initiale non vide), au temps que l'on passe à uriner (situation dynamique), au cas où les hommes font pipi sur un mur plutôt que dans des urinoirs (situation continue), au cas où plusieurs rangées sont disponibles (plusieurs dimensions). Le sujet est vaste !
Le problème de l'urinoir est encore sur bien des points une question ouverte, et terriblement d'actualité !
Et la semaine prochaine, je ne parlerai pas du problème du papier toilette (3), de Donald Knuth...
Notes de bas de page :
(1) Papier pris au hasard sur arXiv : Lower and upper bounds for the first eigenvalue of nonlocal diffusion problems in the whole space et The Schur-Horn theorem for operators with finite spectrum.
(2) The Urinal Problem, par Evangelos Kranakis and Danny Krizanc
(3) The toilet paper problem, par Donald Knuth
(*) Illustration des toilettes : Norbert Nagel



/http%3A%2F%2Fstorage.canalblog.com%2F38%2F13%2F210892%2F99552251_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F93%2F48%2F210892%2F89760281_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F62%2F76%2F210892%2F88024191_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F11%2F46%2F210892%2F87126295_o.jpg)