Szemerédi, go !
Après un mois d'hibernation, je me dois de réouvrir le blog pour annoncer quelque chose de très important : il s'est passé quelque chose sur la planète maths ! Le 22 mars dernier, un prix mathématique a été remis, et pas n'importe lequel : le prix Abel. Et pour la deuxième fois, c'est un hongrois qui décroche la récompense suprême : le célèbre Endre Szemerédi !

Endre Szemerédi, regard langoureux, sourire enjoleur.
Faisons bref : le prix Abel, c'est le prix Nobel des mathématiques (à ne pas confondre avec la médaille Fields, qui est aussi le prix Nobel des mathématiques). Remis par l'académie norvégienne des sciences et des lettres, elle récompense ce qui se fait de mieux en matière de mathématiciens vivants. Cette année, c'est donc Endre Szemerédi qui a été récompensé, «pour ses contributions fondamentales aux mathématiques discrètes et à la science de l'informatique théorique, et en reconnaissance du retentissement profond et durable de ces contributions sur la théorie additive des nombres et la théorie ergodique». S'il fallait résumer de manière très grossière, on pourrait dire que sans lui, Internet n'existerait pas (mais on va éviter de faire ce genre de raccourcis).
Le domaine de prédilection de Szemerédi, c'est donc les mathématiques discrètes. Par exemple, pour modéliser les mouvements d'un fluide, on va s'intéresser aux pressions ou aux vitesse de tout points en fonction du temps pour en déduire des équations dans le meilleur des cas différentielles : ça, c'est le travail des mathématiques continues. Le travail de Szemerédi est donc l'exact opposé.
Le théorème de Szemerédi
Avant de parler du théorème, rappelons qu'une progression arithmétique, c'est une suite où chaque pas (la "raison") est de la même longueur. Par exemple, 4; 7; 10; 13; 16; 19; 22 est une suite arithmétique de longueur 7 et de raison 3.
L'œuvre la plus célèbre de Szemerédi restera donc avant tout sa démonstration en 1975 de la conjecture d'Erdős–Turán, énoncée 40 ans plus tôt : toute suite d'entiers de densité non nulle contient une progression arithmétique arbitrairement longue ! Quand on sait à quel point ses prédécesseurs ont galéré sur le cas des progressions arithmétiques de longueur 3 (Roth, 1956) et de longueur 4 (Szemerédi, 1969), il mérite le respect. Trente ans plus tard, ce théorème deviendra le théorème de Green-Tao ("La suite des nombres premiers contient des suites arithmétiques arbitrairement longues.")
Le théorème de Szemerédi, comme celui de Green-Tao, reste un cas particulier d'une conjecture à 3000$ (la conjecture d'Erdõs) : si la série des inverses d'une suite entière positive diverge, alors elle admet une progression arithmétique arbitrairement longue.
Mais au fait, que dit exactement ce théorème ?
Pour le comprendre, prenons une proportion p (par exemple, 40%) et un nombre k (par exemple, 3). Le théorème énonce donc que si l'on prend au moins 40% des nombres entre 1 et N (N étant un nombre assez grand qui dépend de p et de k), on pourra y trouver une progression arithmétique de 3 termes (une suite où la différence entre deux termes consécutifs est constante).
Le nombre N, dans ce cas-là, est 42. Si vous prenez 17 nombres entre 1 et 42, vous serez certain d'y trouver une suite arithmétique de 3 termes ! La preuve en image :
1, 2, 4, 6, 9, 14, 15, 17, 18, 20, 21, 25, 31, 32, 36, 40, 42
(en cherchant un peu, vous ne tarderez pas à en trouver d'autres)
Ce théorème fonctionne pour n'importe quelle proportion p (aussi petite soit-elle), et pour n'importe quelle longueur k (aussi grande soit-elle). Ainsi, en ne gardant que 1% de la totalité des nombres entiers, on peut quand même y trouver des suites arithmétiques de longueur 200.
Le même théorème (démontré également par Szemerédi) existe en deux dimensions : pour une proportion p donnée, on peut trouver une grille assez grande contenant p points dans lequel il existe un "coin" (trois points de coordonnées (x,y), (x+h,y) et (x,y+h)).
Au cours de sa démonstration, Szemerédi démontrera un lemme sur le moment anecdotique, mais qui deviendra finalement encore plus célèbre que le théorème en lui-même : le lemme de régularité. Ce lemme/théorème deviendra central en théorie des graphes, ce qui n'est pas rien.
Le théorème de Ramsey
Si vous réunissez un nombre suffisamment grand de personnes dans un même endroit, alors
- soit il y aura un groupe de s personnes où chacun connaît tous les autres
- soit il y aura un groupe de t personnes où personne ne se connaît.
C'est ce qu'énonce le théorème de Ramsey (bien qu'il ait plutôt parlé de sous-graphes complets monochromatiques d'un graphe complet coloré)
Le nombre de personnes à réunir dépend évidemment de s et de t. Par exemple, dans le cas s=t=3, il faut réunir au moins 6 personnes :
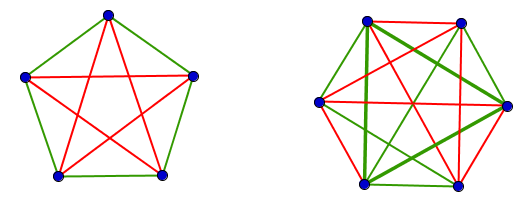
A gauche, une réunion de 5 personnes, à droite, une réunion de 6 personnes
Deux personnes sont reliées en vert si elles se connaissent, en rouge sinon.
A gauche, il n'y a pas de triangle vert (pas de groupes de 3 où tout le monde se connaît), ni de triangle rouge (un groupe de 3 où personne ne connaît personne).
A droite, on trouvera toujours un triangle vert ou un triangle rouge. Ici, trois personnes se connaissent.
Le nombre minimal de personnes a réunir pour qu'il existe un groupe de 4 personnes dans lequel chacun se connaît ou bien personne ne se connaît (cas s=t=4) est 18. Pour s=t=5, ce nombre minimal est quelque part entre 43 et 49, et il semble très difficile d'en avoir une estimation plus précise.
Szemerédi, avec l'aide de Ajtai and Komlós, s'est attelé à chercher une bonne estimation de ce nombre dans le cas s=3 et t quelconque. Leurs conclusions ont plutôt satisfait la communauté.
Le problème des ragots
Bon, on ne va pas s'amuser à lister tous les travaux de Szemerédi, puisqu'il a écrit plus de 200 papiers, qui ont donné des choses très précieuses, comme le théorème de Szemerédi–Trotter, le théorème de Erdős–Szemerédi, le lemme de Balog–Szemerédi–Gowers ou le réseau de tri de Ajtai–Komlós–Szemerédi. Mais j'aimerais parler d'un important papier co-écrit par Szemerédi intitulé "A cure for telephone disease".
Notre prix Abel s'est donc intéressé au problème suivant :
Considérons n femmes, chacune au courant d'un scoop d'envergure mondiale. Lorsque deux femmes se téléphonent, elles se partagent l'ensemble des ragots dont elles ont la connaissance. Combien faudra-t-il au minimum de coups de fil pour que chacune soit au courant de tous les potins ?
Ainsi, si n=1, il faudra 0 coup de téléphone ;
si n=2, il faudra 1 coup de téléphone ;
si n=3, il faudra 3 coups de téléphone ;
si n=4, il faudra 4 coups de téléphone ;
si n=5, il faudra 6 coups de téléphone ;
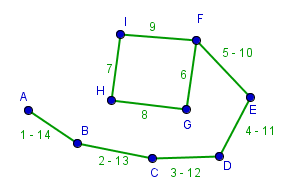
La stratégie la plus efficace pour que 9 femmes se partagent 9 ragots (chaque arête du graphe correspond à un coup de téléphone, le nombre correspond à l'ordre dans lequel il faut les effectuer).
Ils n'ont pas tardé à déterminer la solution tant attendue : au delà de 4 femmes, il faudra 2n-4 coups de téléphone (au minimum) !
Sources :
Site officiel du prix Abel, avec un max d'informations sur Szemerédi
A cure for telephone disease - Hajnal, Milner et Szemerédi



/http%3A%2F%2Fstorage.canalblog.com%2F43%2F78%2F210892%2F106322231_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F66%2F10%2F210892%2F103099174_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F49%2F06%2F210892%2F98803495_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F17%2F55%2F210892%2F98494979_o.jpg)