Erreur des probabilités en votre faveur
"Tiens, et si on se faisait une partie de Monopoly, comme au bon vieux temps ? " Vous ne le savez pas encore, mais en prononçant cette phrase, vous venez d'ouvrir la boîte de Pandore. Ce jeu est de ceux qui font ressortir tout le mauvais enfoui en vous : avidité, manipulation, mauvaise foi... Une seule partie de Monopoly suffit à comprendre les causes de la crise économique.

Mais le Monopoly n'est pas qu'une métaphore du capitalisme, c'est aussi un jeu de société mêlant hasard et stratégie. Mais pour parfaire cette stratégie, il est important de connaître les rouages du jeu. Faut-il tout miser sur les cases bleues, ou s'assurer avec les cases oranges ? Vais-je réellement gagner si je ne possède que la compagnie des eaux ? Mais pourquoi personne ne passe sur les Champs Elysées alors que je passe mon temps sur ton boulevard Henri Martin ?
Bref : sur quelles cases du Monopoly passe-t-on le plus souvent ?
Jouons !
Que l'on joue à l'édition française, à l'édition européenne, à l'édition Montcuq ou à l'édition AC/DC, le plateau reste toujours le même. Quarante cases disposées en carrés, dont 22 propriétés, 4 gares, 2 services publics, 4 chances/caisses de communautés et 7 autres cases plus ou moins heureuses. Pour dépouiller ses adversaires, l'objectif est d'acquérir un maximum de propriétés, sachant qu'un groupe d'une même couleur rapporte plus que des propriétés isolées.
Dans le détail, les 40 cases de l'édition classique française sont les suivantes :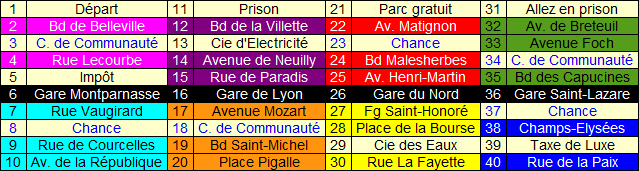
Pour commencer, tous les joueurs se placent sur la case départ, puis on jette les deux dés. On ne s'intéresse qu'au parcours d'un seul joueur, les probas étant indépendantes, et les mêmes pour chaque joueur. Où va arriver le premier joueur ? On calcule facilement que la probabilité que la somme des dés soit 2 ou 12 (resp 3 ou 11, 4 ou 10, 5 ou 9, 6 ou 8, 7) est de 1/36 (resp 2/36, 3/36, 4/36, 5/36, 6/36) ; au premier tour de jeu, le plus probable est donc de tomber sur la case n°8 (chance), puis sur les cases n°7 ou n°9 (bleu clair), etc. (cf les diagrammes un peu plus bas)
Pour le deuxième lancé de dé, on procède de la même façon. Calculons par exemple la probabilité de tomber sur la case n°6 (Gare Montparnasse). On peut arriver sur cette case en faisant 2 (proba : 1/36) depuis la case n°4 (proba : 2/36) ou en faisant 3 (proba : 2/36) depuis la case n°3 (proba : 1/36). On pourrait aussi arriver sur cette case en faisant 4 (proba : 3/36) depuis la case n°1, mais cette dernière a une proba nulle. Finalement, au deuxième tour, la probabilité d'arriver sur la case n°6 est de 1/36×2/36 + 2/36×1/36, ce qui donne 0.3%. (cf les diagrammes un peu plus bas)
De manière générale, pour connaître la probabilité de tomber sur la n-ième case après k lancés, il faut chercher les différentes façons d'atteindre cette case. Dans le cas général, il y a 11 façons d'y arriver : en faisant 2 (proba : 1/36) depuis la case n-2, en faisant 3 (proba : 2/36) depuis la case n-3, etc. La probabilité de tomber sur la case n°n au k-ième lancé de dé est donc de 1/36×pn-2 + 2/36×pn-3 + ... + 1/36×pn-12, où pj désigne la probabilité d'atteindre sur la j-ième case lors du lancé précédent (le (k-1)-ième).
Les calculs deviennent très vite impossibles à faire à la main. Heureusement, l'être humain a inventé l'informatique. Et les matrices stochastiques.
Pour rendre compte de la situation, on utilise la matrice 40x40 suivante :

Le nombre Pi,j (i-ème ligne, j-ième colonne) indique la probabilité d'atteindre la j-ième case depuis la i-ème. Par exemple, la première ligne signifie que, depuis la case n°1, on peut atteindre la case n°3 avec une proba de 1/36, la case n°4 avec une proba de 2/36, etc.
En notant uk le vecteur donnant la probabilité des 40 cases d'être atteintes après k lancés, le vecteur u.P donnera les probabilités des cases au lancé suivant.
Par exemple, la distribution des probas au début du jeu est u0 = [1, 0, 0, ..., 0] (tout le monde est au départ). Au premier lancé, la distribution devient u1 = u0.P. Au k-ième lancé, elle est alors uk = u0.Pk.
En programmant tout ça, on peut calculer ce qu'il se passe après 1, 2, 10 ou 50 lancés :

Distribution des probabilités après 1, 2, 10 ou 50 lancés de dés.
Moralité : plus la partie dure, plus les différentes cases deviennent équiprobables (et se rapprochent de 2,5 %). Autrement dit, aucun groupe de propriétés ne semble meilleur qu'un autre...
En poursuivant les calculs, on se rend compte que les probabilités se stabilisent autour de la distribution équiprobable : c'est la seule distribution qui vérifie u=u.P. (tips : ce vecteur u est le générateur du noyau de t(P-I) )
Ne passez pas par la case départ, ne touchez pas 20 000 F
Mais les déplacements du Monopoly ne sont pas si simples que ça ! Déjà, il y a la case "Allez en prison" (n°31), sur lequel il est impossible de se poser, et qui emmène directement à la case n°11.
De plus, lorsque l'on fait trois doubles de suite (ce qui a 1 chance sur 216 de se produire) , on fait un excès de vitesse : direction la prison !
L'existence de cette case prison change totalement la donne ! Il va falloir refaire tous les calculs. Pas de panique, il suffit juste de modifier la matrice de transition P, et le tour est joué.
Dans les faits : Pour cette histoire de case "aller en prison", il suffit simplement de reporter la colonne n°31 (qui devient nulle) sur la colonne n°11. Pour les excès de vitesse, on supposera qu'il a une chance sur 216 de se produire : dans 215 cas sur 216, on se déplacera à la case normalement (multiplier chaque case par 215/216), sinon, on est amené à la case n°11 (ajouter 1/216 dans la colonne n°11).
Pour connaître les distributions après k lancés, les mêmes calculs que précédement sont à faire :
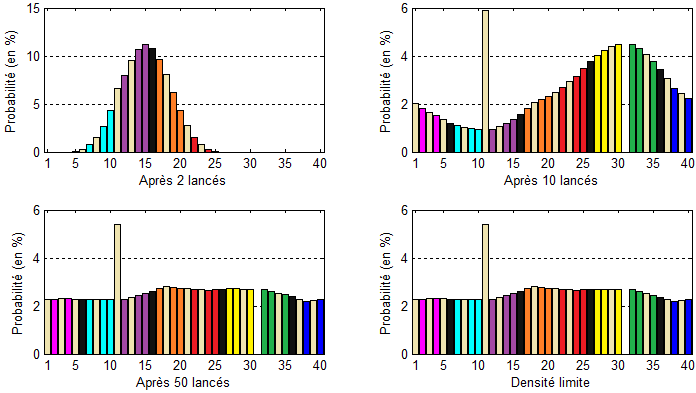
Distribution des probabilités après 2, 10, 50 ou ∞ lancés de dés, en prenant en compte la case "prison"
Finalement, la case prison/visite devient un passage obligé du plateau, les cases suivantes gagnent tout de suite en popularité. Les différentes couleurs ne se valent plus tout à fait, ce qui donne un léger avantage à l'orange, au jaune et au rouge :
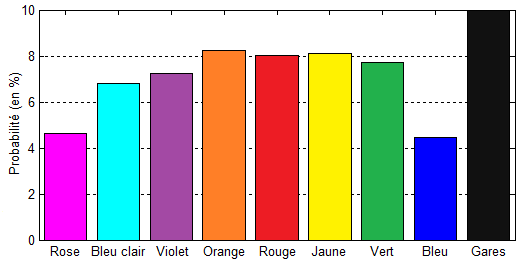
Probabilités de tomber sur les différentes couleurs du jeu, en prenant en compte la case "prison"
Rendez-vous Rue de la Paix
Pour que le modèle soit parfait, il reste deux détails à prendre en compte :
- Les modalités de sortie de prison. En effet, pour retrouver la liberté, il faut impérativement faire un double (au moins pendant deux tours). Du coup, on sort plus souvent de prison en faisant 8 qu'en faisant 7. Dans le modèle, on supposera que l'on sort de prison en faisant un double dans 11 cas sur 36 (probabilité de faire au moins un double en deux lancés), et que l'on sort normalement dans les autres cas.
- Les cartes chances et caisse de communauté. Celles-ci ont tendance à nous emmener en prison, à la case départ ou ailleurs. Dans le détail, sur les 16 cartes chances et les 16 cartes Caisse de communauté, les cartes qui téléportent sont les suivantes :
Cartes chance (cases n°8, n°23 et n°37) :
Allez à la case départ (n°1)
Allez boulevard de la Villette (n°12)
Allez gare de Lyon (n°16)
Allez avenue Henri-Martin (n°25)
Allez en prison (n°31)
Allez rue de la Paix (n°40)
Reculez de trois cases (n°5, n°20 ou n°34)
Cartes caisse de communauté(cases n°3, n°18 et n°34) :
Allez à la case départ (n°1)
Allez Boulevard de Belleville (n°2)
Allez en prison (n°31)
Payez une amende ou piochez une carte chance
La matrice P est à transformer en conséquence. En particulier, il faut prendre en compte le cas où l'on recule sur la case n°34, ce qui a pour effet de piocher une carte Caisse de Communauté. Dans ce modèle on supposera que l'on paye l'amende plutôt que de piocher une carte chance (ça ne change pas grand-chose aux résultats, et j'ai un peu la flemme de le programmer).
Dans les graphiques suivants, on distinguera la case Visite de la prison (n°11) de la case prison (n°31).
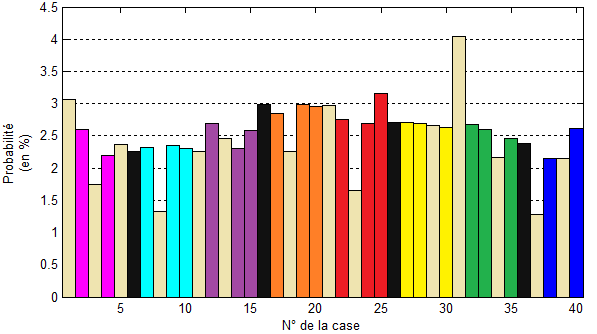
Probabilité de visiter les différentes cases du Monopoly, en prenant en compte toutes les règles
Au final, les cases chances sont les cases sur lesquelles on s'arrête le moins, tandis que la prison reste toujours la plus fréquentée. Du côté des propriétés, seul le boulevard Henri-Martin (n°25) dépasse les 4%, suivi du boulevard Saint-Michel (n°19) et de la place Pigalle (n°20). La propriété la moins fréquentée est alors - et c'est décevant - l'avenue des Champs Elysées (n°38). Les groupes oranges et rouges creusent davantage l'écart, les rendant inévitable pour gagner (surtout que ces rues sont relativement abordables).
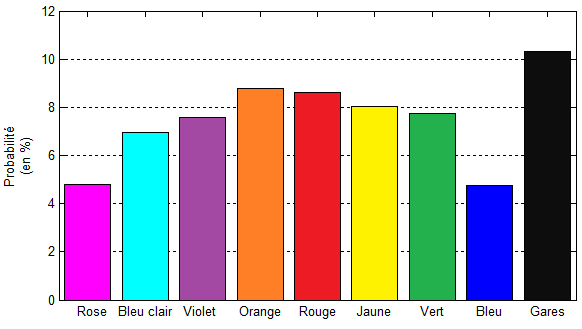
Probabilité de visiter les différentes cases du Monopoly, en prenant en compte toutes les règles
Moralité : on oublie le bleu, et on mise tout sur le orange, le rouge et le jaune. Les probabilités sont de votre côté !
Sources :
Trop monopoly pour être honnête - Ian Stewart - Pour la science n°224 Juin 1996
Comment gagner au monopoly ? - Mémoire de maîtrise, apportant toutes les bases théoriques (chaîne de Markov, etc.)
Si vous voulez analyser les résultats plus en profondeur, et améliorer les usines à gaz que sont mes algorithmes Matlab, voilà de quoi faire : fichier 1, fichier 2 et fichier 42.
Images : Monopoly board



/http%3A%2F%2Fstorage.canalblog.com%2F38%2F13%2F210892%2F99552251_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F93%2F48%2F210892%2F89760281_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F62%2F76%2F210892%2F88024191_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F11%2F46%2F210892%2F87126295_o.jpg)