Bézout futé

Le théorème de Bézout n'est pas qu'un théorème d'arithmétique vu en Terminale, c'est aussi un des principaux résultats de la géométrie algébrique. Ce qui est chouette avec ce résultat, c'est qu'il est manifestement faux au premier abord, mais qu'il devient particulièrement satisfaisant quand on s'y penche un peu. Je ne vais pas le creuser dans cet article, simplement déblayer le terrain. En quelques mots, il dit que :

Deux courbes algébriques de degré n et p ont exactement n×p points d'intersection.

Une courbe algébrique, c'est une courbe dont l'équation est un polynôme (que l'on peut écrire sous la forme P(x,y)=0, comme par exemple 3x³⁶y⁶+4x²y-1=0). Le degré de la courbe, c'est le degré du polynôme. Globalement, les courbes algébriques, c'est ce qui se fait de plus joli en matière de courbes.

A titre d'exemple, les courbes algébriques de degré 1 sont les droites (ax + by + c = 0), celles de degré 2 sont les coniques (paraboles, hyperboles, ellipses...). Plus on grimpe en dégré, plus les courbes sont compliquées à appréhender.

Quelques exemples de courbes algébriques de degré 1 et 2.

Ainsi, d'après le théorème de Bézout, deux droites (degré 1) se coupent toujours en un (=1×1) seul point, deux coniques (degré 2) se coupent toujours en 4 (=2×2) points, une droite (degré 1) coupe toujours une cubique (degré 3) en exactement 3 (=1×3) points...

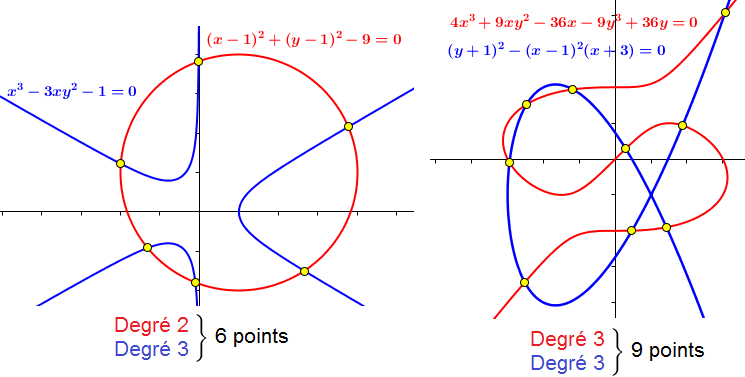
A gauche, l'intersection d'un cercle (degré 2) et d'une cubique de Humbert (degré 3) donne 6 points d'intersection
A droite, l'intersection de deux cubiques (de degré 3) donne 9 points d'intersection

Mais ça, c'est ce qu'il se passe dans un monde parfait. Les contre-exemples sont malheureusement légion :

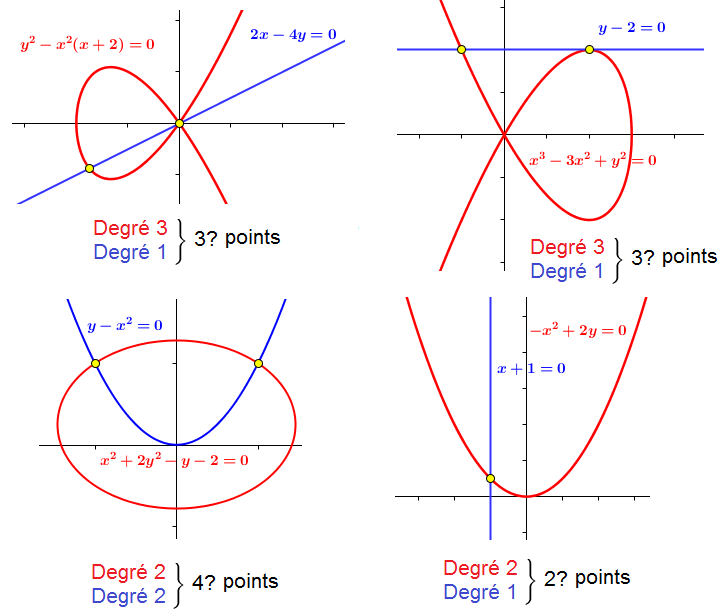
Quatre contre-exemples au théorème de Bézout.

Et pourtant, dans chaque cas, le nombre de points annoncé est bien le bon. Il y a cependant de nombreuses subtilités...

Sauf que... la multiplicité
Dans certains cas, un même point d'intersection comptera plusieurs fois (on parle de la multiplicité de ce point d'intersection). C'est injuste, mais il faut faire avec. Cette situation peut arriver sous plusieurs formes différentes.

Déjà, il y a les courbes qui s'auto-intersectent. C'est par exemple le cas de la cubique x³ - 3x² + y² = 0 (représentée dans le premier contre-exemple), dont la courbe forme une boucle. Au point (0,0), la courbe s'auto-coupe, ce point là sera donc compté deux fois s'il intervient dans une intersection.

Le point (0,0) appartient à la fois à l'arc vert et à l'arc jaune, il sera donc compté deux fois, ce qui donne bien trois points d'intersection.
Remarquons que si on déplace un peu la droite bleue, on retrouve trois vrais points d'intersection.

Lorsque les courbes se touchent sans se croiser, on tombe aussi sur des points comptés double (voire pire). En particulier, c'est ce qui se passe lorsque l'on compte le nombre de point d'intersection entre une courbe et l'une de ses tangentes. 

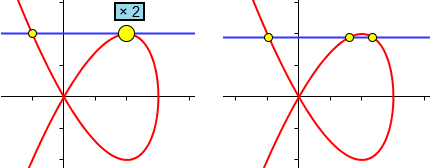
La droite bleue est tangente à la courbe rouge au point (2,2), ce point d'intersection comptera double.
En déplaçant un peu la droite, on peut faire apparaître ces deux points.

Le théorème de Bézout est en fait:

Deux courbes algébriques de degré n et p ont exactement n×p points d'intersection, comptés avec leur multiplicité.

Sauf que... les nombres complexes
Le problème de la représentation graphique des courbes algébriques, c'est qu'elles ne sont que la partie émergée de l'iceberg. Rien n'oblige les courbes à se croiser dans le plan réel, les points d'intersection peuvent parfaitement être complexes. Et cette situation arrive bien trop souvent pour être négligée.

On peut reprendre l'exemple des points d'intersection de la parabole d'équation y-x²=0 et de l'ellipse d'équation x²+2y²-y-2=0. Les points (-1;1) et (1;1) sont solutions, mais les points (i;-1) et (-i;-1) aussi (vérifiez par le calcul si vous ne me croyez pas !). On a bien les quatre points attendus.

En comptant les points à coordonnées complexes, on a bien 4 points d'intersection.

Le théorème de Bézout est en fait :

Deux courbes algébriques de degré n et p ont exactement n×p points d'intersection dans le plan complexe ℂ² , comptés avec leur multiplicité.

Sauf que... les points à l'infini
Où se coupent deux droites parallèles ? Eh bien, elles se croisent... à l'infini ! Pour le voir, il suffit de pencher un peu la caméra pour regarder ce qu'il se passe au loin. En faisant cela, on fait apparaître la ligne d'horizon, où se rencontrent toutes les droites parallèles.

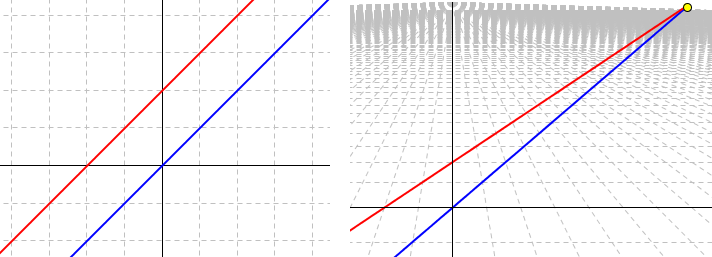
A gauche : deux droites parallèles, vu de dessus
A droite : deux droites parallèles, vu de biais

Ces deux droites, courbes algébriques de degré 1, possèdent donc bien un unique point d'intersection, mais il est "à l'infini". Ce point d'intersection n'est pas dans le plan, mais dans le plan projectif, où l'on a ajouté tous les points à l'infini (chaque point à l'infini correspond à une direction de droite).

De la même façon, on peut voir que la droite et la parabole du premier exemple possèdent bien deux points d'intersection, dont un à l'infini :

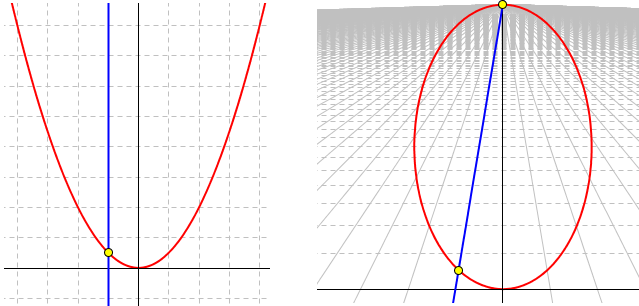
En penchant la caméra, la parabole devient une ellipse, faisant apparaître un deuxième point d'intersection à l'infini. On peut en fait démontrer que n'importe quelle conique est une ellipse, pourvu qu'on la regarde sous le bon angle.

C'est aussi ce qui arrive lorsque deux courbes sont asymptotes l'une à l'autre : elle se croisent sur la ligne de l'infini (et en plus, le point d'intersection sera de multiplicité 2 ou plus).

Le théorème de Bézout est en fait :

Deux courbes algébriques de degré n et p ont exactement n×p points d'intersection dans le plan projectif complexe P₂(ℂ) , comptés avec leur multiplicité.

Sauf que... des composantes communes
Un dernier point à vérifier pour que le théorème fonctionne parfaitement : il ne faut pas que les courbes aient des composantes communes.

Par exemple, prenons les courbes (de degré 2) d'équation x² - 1 = 0 et xy-x-y+1=0. Selon Bézout, ces courbes devraient avoir 4 points en commun. En réalité, ces courbes ont une infinité de points d'intersection :

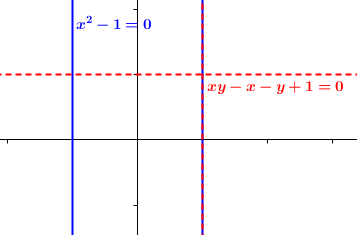
Les deux courbes ont une composante commune, la droite verticale d'équation x=1, qui correspond donc à une infinité de points en commun.

Le problème, c'est que les courbes en question peuvent être écrites comme la réunion de courbes de degré plus petit (des composantes irréductibles). La première est la réunion des droites d'équation x-1=0 et x+1=0, la deuxième est la réunion des droites d'équation x-1=0 et y-1=0. Les deux courbes ont une même composante commune (x-1=0), et le théorème de Bézout n'est pas prévu pour ça.

Le théorème de Bézout est en fait :

Deux courbes algébriques sans composantes communes de degré n et p ont exactement n×p points d'intersection dans le plan projectif complexe P₂(ℂ) , comptés avec leur multiplicité.

Maintenant, on peut appliquer le théorème, et jouer au jeu pratiqué dans le cercle très fermé des géomètres algébristes : "où sont passés les points d'intersection manquant ?!".

Par exemple, combien de points d'intersection possèdent ce quadrifolim (en bleu), de degré 6, et ce trifolium (en rouge), de degré 4 ?

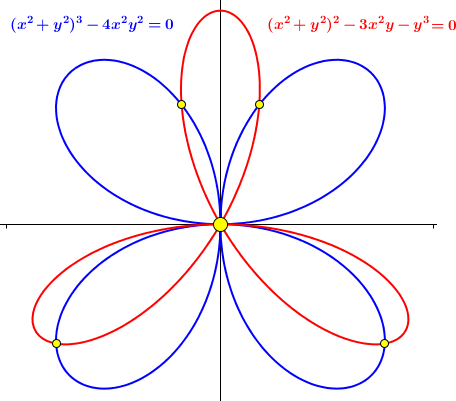
A première vue, on compte 5 points d'intersection, mais il y en a en fait 24 :
4 points réels, de multiplicité 1
1 point réel, de multiplicité 14
2 points complexes à l'infini (les deux à la fois !), de multiplicité 3

(Et joyeux anniversaire à ce blog, qui vient de fêter ses 7 ans !)

---

A lire également :
Bézout et les intersections de courbes algébriques, sur BibNum, analyse de Liliane Alfonsi du texte original de Bézout.

Comments

[Robin]

Très bon. Je m'y suis repris à trois fois pour compter la multiplicité 14, mais faut dire que c'est la première fois que je joue à ce jeu ! Je suis d'accord avec le premier commentaire, c'est un hyper bon exemple pour le passage de l'intuition au formalisme, et pour le fait que quand un résultat est pratique, on fera tout pour le garder !

Je ne sais pas si j'arriverai à le ressortir un jour au bon moment et au bon endroit, mais je garde l'idée, merci

[Petouche]

j'admire le jeu de mot dans le titre :)



sinon excellent comme toujours

[Bob]

Bravo pour cet excellent article, et ses superbes figures !

[michel]

Depuis quand deux droites se coupent toujours en un point ? Je taquine mais ça méritait d'être dit !

[David]

Joyeux anniversaire !