Indivisibles
Tout bon agenda de lycéen comporte une page regroupant les formules d'aires et de volumes des figures usuelles. Certaines formules coulent de sens (aire d'un carré, d'un rectangle), d'autres sont évidentes si on prend deux secondes pour y réfléchir (aire d'un triangle, d'un parallélogramme). Et il y a les autres, qui semblent sortir de nulle part : pourquoi l'aire d'un disque de rayon r est πr² ? Et pourquoi le volume d'une sphère est de 4/3 π r3 ?
Ces formules ont été découvertes assez vite, mais au fil de l'histoire, ce sont les démonstrations qui ont évolué. Dans l'antiquité, Euclide et Archimède ont utilisé la méthode d'exhaustion pour prouver l'équivalent de ces formules : l'aire d'un disque ne peut pas être plus grande que πr², elle ne peut pas être plus petite non plus, elle lui est donc égale.
Cette méthode d'exhaustion fait appel aux limites, autrement dit, à l'infini. La notion d'infini étant taboue à l'époque, les calcul d'aires étaient plutôt limités.
Aujourd'hui, pour calculer l'aire ou le volume d'une figure, on utilise l'intégration, qui fait appel à des sommes infinies d'objets infiniment petit. Depuis que l'on sait dompter l'infini, ce genre de calculs ne fait plus peur à qui que ce soit.
Entre temps, il y a eu le XVIIe siècle. A l'époque, l'infini n'était toujours pas parfaitement assimilé, mais plus personne n'avait peur de le manipuler, quitte à faire pleurer n'importe quel mathématicien moderne. C'est à cette période que John Wallis invente le symbole ∞ et que Leibniz et Newton inventent/découvrent le calcul infinitésimal moderne.
Juste avant ces progrès, il y a eu Cavalieri et Roberval, qui ont mis au point une méthode redoutable pour calculer des aires et produire de nouvelles formules. La seule ombre, c'est que cette méthode miracle ne fonctionne pas dans toutes les situations, sans que l'on ne sache exactement pourquoi. Aujourd'hui, on le sait : l'infini doit être manipulé avec précaution pour éviter les paradoxes. Il n'empêche, leur méthode fonctionne !
Robin l'avait évoqué dans cet excellent épisode de Podcast Science sur l'infiniment petit, j'ai voulu creuser un peu. La méthode des indivisibles de Cavalieri, ancêtre du calcul intégral, comment ça marche ?
Le principe de Cavalieri
L'idée de base est de considérer une surface comme l'empilement d'un nombre indéfini de lignes, toutes parallèles. Si deux surfaces sont composées de lignes deux à deux de même longueur, alors les surfaces auront la même aire.
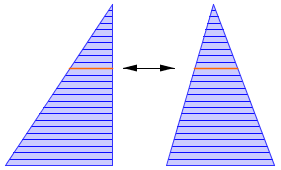
Ces deux triangles sont formés d'un empilement de segments, deux à deux de même longueur. Les deux triangles ont donc la même aire.
Ceci permet de montrer que n'importe quel triangle est équivalent à un triangle rectangle, et donc, d'aire ½ b×h.
Avec cette méthode, pour montrer que deux surfaces ont la même aire, il suffit de montrer que les segments transversaux ont deux à deux la même longueur. La méthode fonctionne également pour le calcul de volumes, comme empilement d'un nombre indéfini de plans.
Ces lignes, on les appelle les "indivisibles". Le gros soucis, c'est que l'on ne comprend pas vraiment leur nature : ce ne sont pas des segments, ce ne sont pas des rectangles, c'est probablement quelque chose entre les deux.
Quadrature de la cycloïde
Le premier morceau de bravoure de cette théorie naissante a été celui de la quadrature de la cycloïde, la courbe qui correspond à la trajectoire d'un point sur le bord d'un disque qui roule :
Fait particulièrement intéressant : l'aire située sous cette courbe correspond à trois fois l'aire du disque qui l'a générée. Ça, c'est Galilée qui l'a découvert, après avoir construit et pesé des cycloïdes en métal. Il a cependant refusé de croire que ce résultat était correct, et a conclu à une erreur de mesure (1599). Le premier calcul de cette aire est dû à Roberval, grâce à la méthode de Cavalieri (qui était un étudiant de Galilée).
Pour cela, nous avons besoin :
- du cercle générateur, en vert, d'aire Adisque = πr²
- de la cycloïde, en bleue
- de sa courbe "compagnon", en rouge, définie à partir du cercle générateur de la façon suivante : pour un point A du cercle, on construit le point M à la même hauteur de A, et dont l'abscisse 0N est égale à la longueur de l'arc de cercle 0A.
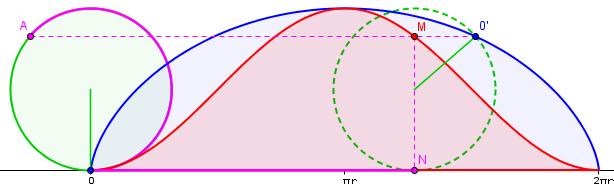
Disque générateur en vert (de rayon r, donc de circonférence 2πr)
Cycloïde en bleu. Après déplacement du disque, le point 0 se retrouve en position 0'.
Courbe compagnon en rouge. Par construction, la longueur 0N est égale à la longueur de l'arc violet 0A.
On peut alors montrer que :
- les portions situées entre la cycloïde et sa courbe compagnon ont chacun l'aire d'un demi disque.
- l'aire sous la courbe compagnon est égale au double de celle du disque.
Finalement, l'aire sous la cycloïde est égale à l'aire de trois disques.
* Aentre les courbes = ½ Adisque
On utilise ici la méthode de Cavalieri. Les segments du demi-disque sont de même longueur que ceux de l'entre-deux courbes, les aires sont donc égales.
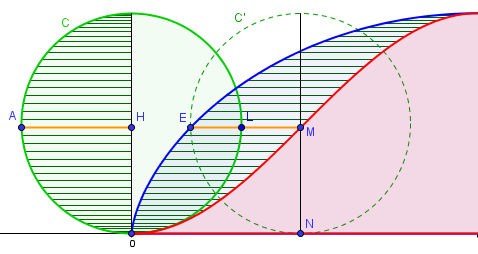Les segments à hauteur égale sont de même longueur. D'après la méthode de Cavalieri, les deux aires hachurées sont égales.
Sur le schéma ci-dessus, on prend un point A sur le cercle C, et on considère les points H, E et M à hauteur de A sur, respectivement, le diamètre vertical du cercle C, sur la cycloïde et sur la courbe compagnon. Il s'agit de montrer que AH = EM. Pour cela, on considère le point L, intersection du cercle C et de EM (lui aussi, à hauteur de A). Lorsqu'on fait tourner le cercle C pour qu'il aille en position C', puisque les arcs 0L=0A=0N, L est envoyé sur N, et donc, 0 est envoyé sur E (car 0L=EN). Donc le point E appartient au cercle C'. Le cercle C' peut alors être vu comme le translaté de C, de même pour les segments AH et EM : ils sont donc identiques.
* Acompagnon = 2 Adisque
On se place dans le rectangle (0,0),(πr,0),(πr,2r),(0,2r), d'aire b×h = πr×2r = 2πr².
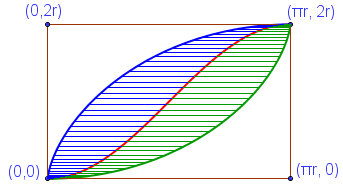La courbe compagnon est symétrique !
Il suffit alors de remarquer que la courbe compagnon est symétrique par rapport au centre de ce rectangle (pour s'en convaincre, on peut tracer une deuxième cycloïde), elle le coupe donc en deux parts égales. Donc l'aire sous cette demie courbe compagnon est πr², qui est l'aire du disque.
Bref : l'aire de la cycloïde, c'est trois fois l'aire du disque. Yeah !
Quadrature du cercle
La méthode de Cavalieri fonctionne aussi lorsque les lignes ne sont pas des segments. Il faut évidemment prendre encore plus de pincettes, mais cela donne une méthode assez intuitive permettant de calculer l'aire du disque.
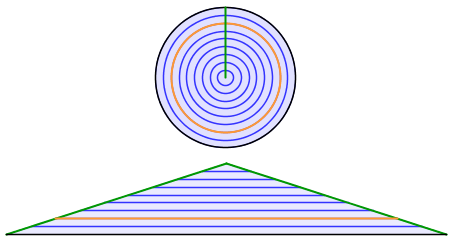Pour calculer l'aire d'un cercle de rayon r, on considère tous les cercles concentriques de rayons k ≤ r. Chacun de ces cercles a une circonférence égale à 2πk. On redresse alors tous ces cercles : on obtient un triangle isocèle de base b = 2πr (la circonférence du disque initial), et de hauteur h = r (le rayon du disque initial).
L'aire de ce triangle est alors de b × h ÷ 2 = 2πr × r ÷ 2 = πr². Yeah !
La quadrature ratée du triangle
Parlons tout de même de ce qui fâche : la méthode de Cavalieri ne fonctionne pas dans tous les cas. Ce n'est pas parce que les lignes sont deux à deux de même longueur que les aires seront égales. On sent bien, sur l'exemple ci-dessous, qu'il y a "plus" de lignes dans le premier triangle que dans le deuxième...
Les deux segments oranges sont de même longueur, les deux rectangles devraient avoir la même aire...
Quadrature du rouleau de PQ
En s'inspirant du calcul de l'aire du disque par la méthode de Cavalieri, on peut en déduire une excellente méthode permettant de calculer le nombre de feuilles de papier toilette dans un rouleau. La principale différence d'avec la méthode de Cavalieri, c'est que les feuilles de papier toilette ne sont pas infiniment fine (et heureusement).
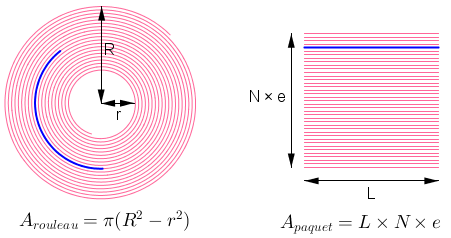
Il suffit finalement de se rendre compte que, en redressant chacune des feuilles du rouleau, on obtient un paquet de feuilles, rectangulaire. En notant R (resp. r) le rayon du rouleau plein (resp. vide), l'aire latérale du rouleau est π(R²-r²). En notant L la longueur d'une feuille, N le nombre de feuilles dans un rouleau et e son épaisseur, on trouve que l'aire du paquet est LNe.
D'après Cavalieri, les deux aires sont égales, donc le nombre N de feuilles dans un rouleau de papier toilette est donné par...
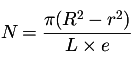
Ce qui, pour R = 4.5 cm, r = 2 cm, L = 12.5 cm et e = 0.015 cm, nous donne environ 270 feuilles. Yeah !
Sources :
Cycloids and Paths : Tout sur la cycloïde
Méthode des indivisibles, sur Wikipedia
Images :
Cycloid
/http%3A%2F%2Fstorage.canalblog.com%2F83%2F26%2F210892%2F75334806_o.gif)
/http%3A%2F%2Fstorage.canalblog.com%2F67%2F30%2F210892%2F50011149_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F68%2F20%2F210892%2F46362948_o.jpg)
/http%3A%2F%2Fstorage.canalblog.com%2F15%2F22%2F210892%2F39650212_o.png)
