Le cavalier d'Euler

En ce 300e anniversaire de la naissance d'Euler, le mathématicien qui a tout fait en mathématiques, j'aimerais jouer à un jeu... Ce jeu, c'est celui du cavalier d'Euler (alias "le problème du cavalier", "le cavalier polygraphe" ou "la polygraphie du cavalier"), étudié par Euler en 1759 (car, je le rappelle, il a tout étudié)

Pour jouer, il suffit d'un échiquier de 64 cases et d'un cavalier (vendu avec l'échiquier). Le principe est simple : avec le mouvement en L spécifique du cavalier, il faut parvenir à passer sur toutes les cases de l'échiquier de manière unique. Vous pouvez le tester derrière ce lien.

Vous avez trouvé une solution ?! Félicitations ! Mais ce n'est pas tout d'en avoir une seule, ça serait quand même plus rigolo de toutes les avoir, non... On peut donc légitimement se poser la question du nombrede parcours possibles.
En 1995, deux chercheurs allemands, Martin Löbbing et Ingo Wegener, font tourner 20 puissants ordinateurs pendant 4 mois, et arrivent au chiffre de 33 439 123 484 294 parcours possibles... Mais après une petite réflexion, ils remarquent qu'une erreur s'était glissée dans leur raisonnement, et que finalement, les quatre mois de calculs n'ont servi à rien du tout...
En 1997, Brendan McKay, chercheur australien de son état, fait un travail un peu plus sérieux, et trouve le chiffre de 13 267 364 410 532 circuits.
Mais ces chiffres, ce n'est que pour les circuits fermés, c'est à dire, ceux qui reviennent à la case départ...

Alors, combien de circuits possibles ?!

En 2001, le chiffre tombe : 1,22 millions de milliards de possibilités, c'est à dire 1 220 000 000 000 000 possibilités. Pour se donner une idée, si un ordinateur donnait un millions de solutions par secondes, il faudrait dans les 40 ans pour avoir toutes les solutions. Évidemment, ce chiffre ne tient pas compte des possibilités de symétries...

Après, on peut s'amuser à changer la taille ou la forme de l'échiquier, et c'est parti pour de nombreuses heures de fun en perspectives. Par contre, si vous voulez vraiment trouver des solutions excluez les échiquiers de moins de 6×6 cases. Si vous cherchez des solutions qui reviennent à la case départ, il faut un nombre pair de cases.

La première solution de ce sympathique jeu nous est donné par al-Adli ar-Rumi en l'année 840 :

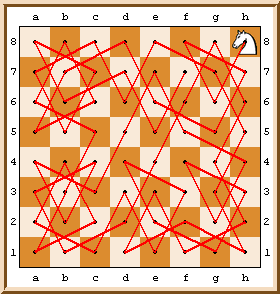
Et reste la question : pourquoi je vous parle de tout ça ? Et bien, tout simplement pour commencer une série de notes sur la théorie des graphes, qui va peut-être nous amener à résoudre le problème P=NP (ou pas)...

En fait, ce problème revient à chercher un parcours hamiltonien au sein de ce graphe : (mais j'y reviendrais lors de prochaines notes, histoire d'expliquer ce que veut dire parcours hamiltonien).

---

Sources :
Cet excellent article de procrastin
Et un peu wikipedia

Comments

[badr]

salut El Jj je suis vraiment très interessé par l'etude mathématique du déplacement du cavalier sur des parcours fermé ou normal j'aurai bien voulu que tu m'envoie ton adresse email et ton numero pour te contacter merci d'avance

badr

[blop]

A signaler que dans "la vie mode d'emploi", Perec divise la maison qui sert de decor a l'histoire en un damier (10x10) ou chaque case correspond a une piece (de la cave au grenier), ou chaque chapitre est consacre a une case et ou les chapitres se suivent... selon le probleme du cavalier !

[Enro]

Bonjour El Jj, je cherche à te contacter mais pas moyen de mettre la main sur ton adresse... Peux-tu m'envoyer un mail s'il te plaît ? Merci d'avance !

[procrastin]

héhé, content de voir que le billet t'a plu :)

[abricot]

Et pour rigoler on calcule la matrice à la main ! ^^