Du choix dans la dissection
La quadrature du cercle (Selon Tarski) est faisable !
Laczkovich a la solution, moyennant des ciseaux fractals, de la patience pour faire 1050 pièces et l'axiome du choix. (C'était la semaine dernière sur ce blog)
Mais l'axiome du choix, c'est quoi ? Et pourquoi permet t'il d'avoir des résultats si bizarres ? Tentative d'explication.
Petits rappels. En maths, les axiomes sont les bases - "évidentes" -
sur lesquelles reposent toutes les théories que l'on peut élaborer.
La
théorie des ensemble repose sur un ensemble de 10 axiomes, appelés axiomes de la théorie ZFC (par exemple
"il existe un ensemble vide", "deux ensembles qui possèdent les mêmes
éléments sont identiques", "Deux objets forment une paire" etc.).
L'un
de ces axiome est l'axiome du choix. L'idée de cet axiome, c'est que si
on dispose d'une commode avec des tiroirs, on peut prendre un objet par
tiroir, et former avec un nouvel ensemble d'objet. Évidemment, cela
pose problème quand le nombre de tiroir est infini, et que le nombre
d'objets dans ces tiroirs est également infini...
Cet axiome du
choix est un grand sujet de polémique dans le milieu des
mathématiciens, vu les résultats comme celui de Lackovich qu'il peut
apporter.
Le paradoxe de Banach-Tarski... (tadadam)
Avec 3 dimensions, c'est encore pire, avec le paradoxe de Banach-Tarski (Qui n'est pas un paradoxe en tant que tel, c'est juste un résultat choquant)
Prenez une sphère
Découpez-la en 5 morceaux selon les plans de Banach et Tarski
Prenez d'un côté les deux premiers morceaux, de l'autre les 3 autres et rassemblez-les.
Vous avez maintenant 2 sphères, chacune ayant le même volume que la première !
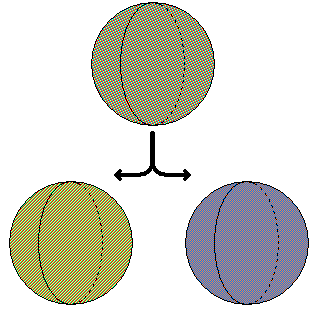
Selon ce plan de découpage, il est donc mathématiquement possible de dédoubler à l'infini une sphère en or. Le même énoncé permet de dire également que l'on peut théoriquement découper un petit pois d'une certaine façon qui, après réassemblage, formerait une sphère de la taille du Soleil. (Il faut noter au passage que s'imaginer ce "plan" de découpage est quelque chose encore plus difficile à faire que de se représenter l'ensemble des rationnels ou d'imaginer une couleur qui n'existe pas)
Évidement, si c'était faisable dans la réalité physique du monde, ça se saurait, alors, il est où, le problème ?
Le paradoxe de Banach-Tarski nous renvoie à notre notion de volume.
Le volume, comme l'aire ou la longueur, sont des mesures, au sens mathématique (une fonction qui, a des ensembles, leur associe un nombre. Si l'ensemble est vide, sa mesure sera 0 ; si deux ensembles sont disjoints, leur mesure pourront s'additionner).
Prenons le cas de la longueur. Tout le monde est d'accord, un point a pour longueur 0. On peut en prendre plusieurs suffisamment éloignés, 0+0=0, cet ensemble de points n'aura toujours pas de longueur.
Quand on en prend une infinité suffisamment rapprochés (continue), on fabrique des segment, et ça, ça possède bien une longueur. Ce qui peut être choquant, c'est qu'en prenant d'une certaine façon une infinité de points, il seront suffisamment proche les uns des autres pour ne pas avoir une mesure nulle, mais suffisamment éloignés les uns des autres pour ne pas former quelque chose de continu, et donc, auquel on ne pourra pas associer de longueur.
Ce que nous dit Banach et Tarski, c'est qu'il est théoriquement possible de prendre des ensembles de points de l'espace de manière à ce que la notion de volume n'ait même plus de sens ! En découpant la sphère avec des morceaux pour lesquels le volume n'a pas de sens, il n'est pas du tout impossible qu'en les recombinant, on retrouve quelque chose de mesurable, mais de mesure différente !
Mais pour réaliser ce prodige, l'axiome du choix est nécessaire. C'est la deuxième fois que cet axiome nous apporte un théorème totalement contre intuitif, et pour certains mathématiciens, c'en est trop ! Si ça se trouve, en continuant comme ça, on en arriverait à démontrer quelque chose ainsi que son contraire. En enlevant cet axiome, peut-être risque t'on moins ce genre de désagrément futur ?...
Il y a 60 ans, Gödel s'est intéressé à la question : l'ensemble des axiomes de la théorie des ensemble peut-il amener à des théorèmes contradictoire ? Une chose est sûre, c'est qu'il y a des théorème indécidables : on ne peut ni les démontrer, ni les réfuter. Pour ce qui est de la non contradiction de l'ensemble des axiomes, c'est plus compliqué.
Heureusement, Gödel a réussit à démontrer quelque chose de chouette : l'ensemble des axiomes de la théorie des ensembles (avec axiome du choix) est contradictoire si et seulement si l'ensemble des axiomes de la théorie des ensemble (sans l'axiome du choix) est contradictoire...
Moralité : on est pas plus avancé, mais ya aucune raison de se passer de ce bel axiome, et tant pis si les résultats sont contre-intuitif !
Est-ce là la limite entre les maths et la physique ?... Oui, peut-être...
Attention : ne pas confondre le paradoxe de Banach-Tarski et celui de Bananach-Tarski :
Sources :
Les découpages artistiques - Pour la science n°257, mars 1999 (On ne change pas une revue qui marche)
Wikipédia - Un exemple -relativement simple- d'ensemble non mesurable.
Le paradoxe de Banach-Tarski [pdf]



/http%3A%2F%2Fstorage.canalblog.com%2F70%2F81%2F210892%2F112209252_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F33%2F48%2F210892%2F109066358_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F58%2F95%2F210892%2F102067299_o.png)
/http%3A%2F%2Fstorage.canalblog.com%2F85%2F70%2F210892%2F65561362_o.png)